提示：该Blog仅用于作业汇报展示，大佬请绕路

文章目录

一、作业介绍
二、数据处理
三、数据分析
四、特征选择
五、模型训练与评价
六、模型优化
七、与原模型进行对比
八、作业总结

一、作业介绍

该项目依托于某医院处理好之后的体检数据，首先进行了一些简单的数据分析，然后使用多重线性分析法、递归特征消除法、正则化法三种方法对数据进行特征选择，选择出了预测相关度最高的几个属性，以此来分别训练Logistic、SVM、XGBoost三种算法模型，观察其训练效果，最后再进行模型调参，观察调参前后的训练效果。

二、数据处理

先导入所要用到的包

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sn
from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression
from sklearn import preprocessing
from sklearn.svm import SVC, LinearSVC
from sklearn.feature_selection import SelectFromModel
from sklearn.metrics import confusion_matrix
from sklearn.metrics import f1_score
from sklearn.metrics import roc_curve,auc
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.model_selection import train_test_split
from xgboost import XGBClassifier
from sklearn.model_selection import GridSearchCV
import warnings

先粗略观察了一下数据

# 查看数据的前五行数据
dataConcat.head()

在这里插入图片描述

查看有多少行数据、多少个特征值

# 查看数据总共有多少行，多少个特征值
dataConcat.shape
结果：(1006, 16)

查看数据特征的具体的信息

# 查看数据详细的详细
dataConcat.info()

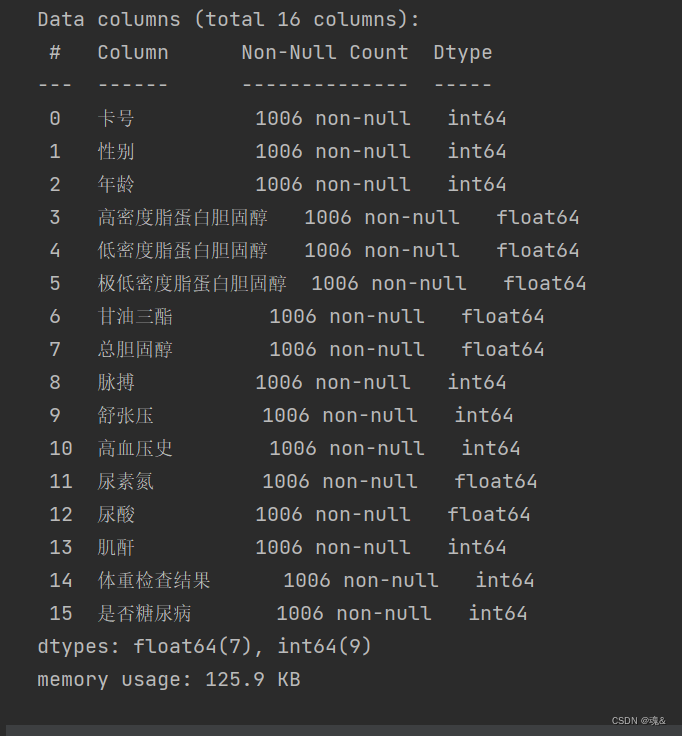
在这里插入图片描述
由此可以看出，数据完整，没有缺失值。

数据分桶

# 为了后续更好的将数据输入机器学习模型，有必要将某些数据列进行分桶，也就是划分区间
# 选取年龄这个特征值
age = dataConcat['年龄']
# 开始对数据进行分桶
# 将年龄分为四个区间,(0,30),(30,45)(45,60)(60,100),并将四个区间的标签设置为0,1,2,3
age_binary = pd.cut(age,[0,30,45,60,100],labels=[0,1,2,3],right=False)

将分桶后的数据添加回源数据

dataConcat['年龄_cut'] = age_binary
# 因为添加减去的数据类型为category，所有要做一次数据转换
dataConcat['年龄_cut'] = dataConcat['年龄_cut'].astype('float')

对脉搏和舒展压力进行相同的处理

# 接下来对脉搏和舒展压进行与年龄相同的数据处理
pulse = dataConcat['脉搏']
pulse_binary = pd.cut(pulse,[0,60,99,200],labels=[0,1,2],right=False)
dataConcat['脉搏'] = pulse_binary
dataConcat['脉搏'] = dataConcat['脉搏'].astype('float')pressure = dataConcat['舒张压']
pressure_binary = pd.cut(pressure,[0,60,89,200],labels=[0,1,2],right=False)
dataConcat['舒张压'] = pressure_binary
dataConcat['舒张压'] = dataConcat['舒张压'].astype('float')

三、数据分析

观察不同BMI指数的正常人与糖尿病人的比例

# 设置画布大小
fig=plt.figure(figsize=(12,30))
# 调整子图内部间距
plt.subplots_adjust(wspace=0.4,hspace=0.4)
# subplot2gird() 函数以非等分的形式对画布进行切分，并按照绘图区域的大小来展示最终绘图结果,这里设置为5行2列的画布,并开始第一个子图绘制
a1 = plt.subplot2grid((5,2),(0,0),colspan=2)
# 统计没有患糖尿病的人的体重分布数量
diabetes_0_1 = dataConcat.体重检查结果[dataConcat.是否糖尿病 == 0].value_counts()
# 统计患糖尿病的人的体重分布数量
diabetes_1_1 = dataConcat.体重检查结果[dataConcat.是否糖尿病 == 1].value_counts()
# 将diabetes_0_1和iabetes_1_1组合成一个Dataframe
df1 = pd.DataFrame({'糖尿病患者':diabetes_1_1,'正常人':diabetes_0_1})
# 由于患糖尿病的人没有偏瘦的人的存在,所以在将数据组合成DataFrame时糖尿病患者那一列存在空值,不利于之后画图,所以再次处理一下空值
df1['糖尿病患者'].fillna(0,inplace=True)
# 进行值的映射,源数据的0,1,2,3分别表示较瘦,正常,偏重,肥胖
weight_map={0:'较瘦',1:'正常',2:'偏重',3:'肥胖'}
df1.index = df1.index.map(weight_map)
# 绘制直方图
index = ['较瘦','正常','偏重','肥胖']
plt.bar(df1.index,df1['正常人']+df1['糖尿病患者'])
plt.bar(df1.index,df1['糖尿病患者'])
# plt.bar(['较瘦','正常','偏重','肥胖'],df1['正常人'])
plt.title(u"BMI不同的人患糖尿病情况")
plt.xlabel(u"体重检查结果")
plt.ylabel(u"人数")
plt.legend((u'正常人', u'糖尿病'),loc='best')
df1

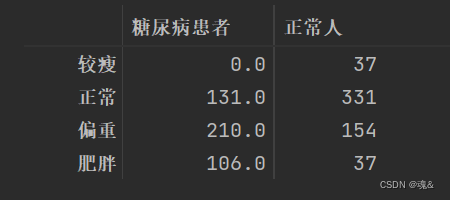
在这里插入图片描述

可以看出，糖尿病人的BMI指数明显偏高

查看男女患病情况

# 在男女患病情况进行查看,步骤与上基本一致
diabetes_0 = dataConcat.性别[dataConcat.是否糖尿病 == 0].value_counts()
diabetes_1 = dataConcat.性别[dataConcat.是否糖尿病 == 1].value_counts()
df2 = pd.DataFrame({'糖尿病患者':diabetes_1,'正常人':diabetes_0})
sex_map={1:'男',0:'女'}
df2.index = df2.index.map(sex_map)
plt.bar(['男','女'],df2['糖尿病患者'])
plt.bar(['男','女'],df2['正常人'],bottom=list(df2.loc[:,'糖尿病患者']))
plt.title(u"男女患糖尿病情况")
plt.xlabel(u"性别")
plt.ylabel(u"人数")
plt.legend((u'糖尿病', u'正常人'),loc='best')

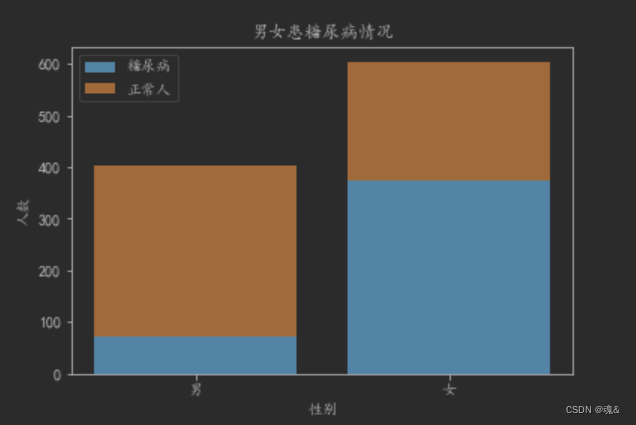
在这里插入图片描述
可以看出女性患糖尿病的比例明显比男性要高

糖尿病人与正常人年龄分布情况

dataConcat.年龄[dataConcat.是否糖尿病 == 1].plot(kind='kde')
dataConcat.年龄[dataConcat.是否糖尿病 == 0].plot(kind='kde')
plt.xlabel(u"年龄")# plots an axis lable
plt.ylabel(u"密度")
plt.title(u"糖尿病和正常人年龄分布")
plt.legend((u'糖尿病', u'正常人'),loc='best')

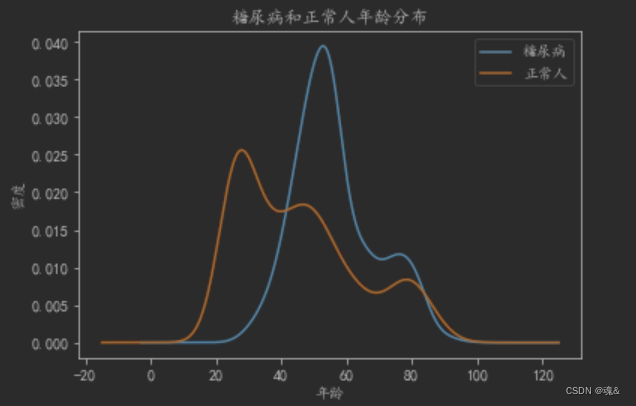
在这里插入图片描述
可以看出患糖尿病的人大多是都是年龄较高的人

其他的一些特征分析

# 绘制低密度脂蛋白胆固醇密度曲线
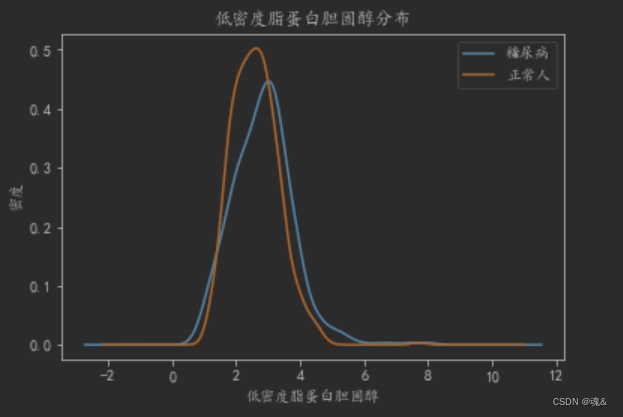
dataConcat.低密度脂蛋白胆固醇[dataConcat.是否糖尿病 == 1].plot(kind='kde')
dataConcat.低密度脂蛋白胆固醇[dataConcat.是否糖尿病 == 0].plot(kind='kde')
plt.xlabel(u"低密度脂蛋白胆固醇")# plots an axis lable
plt.ylabel(u"密度")
plt.title(u"低密度脂蛋白胆固醇分布")
plt.legend((u'糖尿病', u'正常人'),loc='best')

在这里插入图片描述

# 绘制高密度脂蛋白胆固醇密度曲线
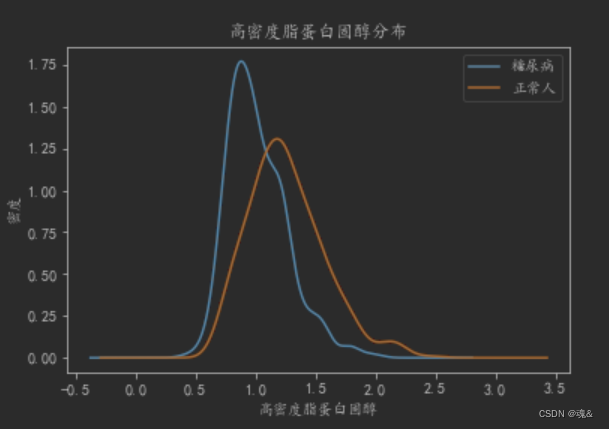
dataConcat.高密度脂蛋白胆固醇[dataConcat.是否糖尿病==1].plot(kind='kde')
dataConcat.高密度脂蛋白胆固醇[dataConcat.是否糖尿病 == 0].plot(kind='kde')
plt.xlabel(u'高密度脂蛋白固醇')
plt.ylabel(u'密度')
plt.title(u'高密度脂蛋白固醇分布')
plt.legend((u'糖尿病',u'正常人'),loc='best')

在这里插入图片描述

#绘制尿素氮曲线
dataConcat.尿素氮[dataConcat.是否糖尿病 == 1].plot(kind='kde')
dataConcat.尿素氮[dataConcat.是否糖尿病 == 0].plot(kind='kde')
plt.xlabel(u"尿素氮")# plots an axis lable
plt.ylabel(u"密度")
plt.title(u"尿素氮分布")
plt.legend((u'糖尿病', u'正常人'),loc='best')

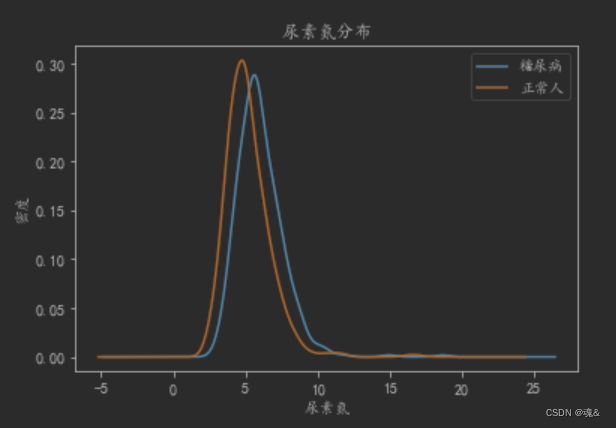
在这里插入图片描述
从上述的基本统计分析，我们可以大致观测出糖尿病人与正常人的一些差异，比如体重指数较高，高密度脂蛋白胆固醇较低，尿素氮和尿酸较高等

四、特征选择

绘制热力图，观察各个属性之间的相关性
相关性系数的取值范围为【-1，1】，绝对值越大，相关性越高，越接近于0，相关系数越低。

plt.figure(figsize=(10,8))
df_cor=dataConcat.iloc[:,1:-1]
df_cor.corr()
data_cor=df_cor.corr()
mask = np.triu(np.ones_like(data_cor, dtype=np.bool))mask = mask[1:, :-1]
corr = data_cor.iloc[1:, :-1].copy()cmap = sns.diverging_palette(0, 230, 90, 60, as_cmap=True)
sns.heatmap(corr,mask=mask, annot=True, fmt=".2f", cmap=cmap,linewidth=3,vmin=-1, vmax=1, cbar_kws={"shrink": .8},square=True)
plt.title('属性热力图')
plt.tight_layout()#调整布局防止显示不全

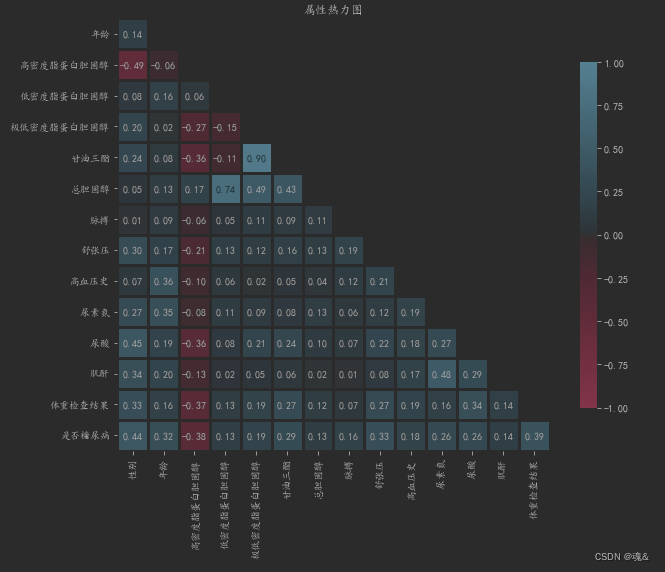
在这里插入图片描述

使用多重线性分析法选择特征值

多重线性分析法

当任何两个特征存在相关性时，就会出现多重线性，而在机器学习中，期望每个特征都应该是独立于其他特征，即每个特征之间没有共线性。
这里采用方差膨胀因子VIF来衡量多重线性，根据以往经验，VIF大于10，则代表特征有较严重的多重共线性。
如果模型仅用于预测，则只要拟合程度好，可不处理多重共线性问题，存在多重共线性的模型用于预测时，往往不影响预测结果

from statsmodels.stats.outliers_influence import variance_inflation_factor
feature_names = ['性别', '年龄_cut', '低密度脂蛋白胆固醇','高密度脂蛋白胆固醇','极低密度脂蛋白胆固醇','甘油三酯', '总胆固醇', '脉搏', '舒张压','高血压史','尿素氮','尿酸','肌酐','体重检查结果']
X=dataConcat[feature_names]
y=dataConcat.是否糖尿病
# 计算 VIF
vif = pd.Series([variance_inflation_factor(X.values, i) for i in range(X.shape[1])], index=X.columns)
# 展示VIF结果
index = X.columns.tolist()
vif_df = pd.DataFrame(vif, index = index, columns = ['vif']).sort_values(by = 'vif', ascending=False)
vif_df

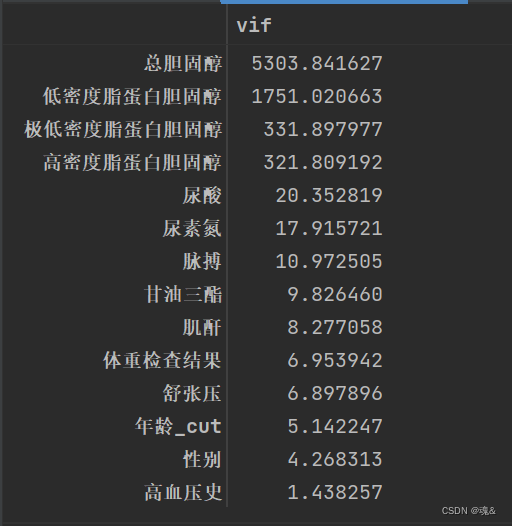
在这里插入图片描述

递归特征消除法
它通过模型训练样本，然后对每个特征进行得分进行排序，去掉最小特征得分的特征，然后用剩余的特征再次训练模型，进行下一次迭代，最后选出需要的特征数。

#递归特征消除法，返回特征选择后的数据
#参数estimator为基模型
#参数n_features_to_select为选择的特征个数
min_max_scaler1 = preprocessing.MinMaxScaler()
# 进行归一化处理
X_train_minmax1 = min_max_scaler1.fit_transform(dataConcat[feature_names])#特征归一化处理
svc = SVC(kernel="linear")
selector=RFE(estimator=svc, n_features_to_select=8)
Xt=selector.fit_transform(X_train_minmax1,dataConcat.是否糖尿病)
print("N_features %s" % selector.n_features_) # 保留的特征数
print("Support is %s" % selector.support_) # 是否保留
print("Ranking %s" % selector.ranking_) # 重要程度排名
for i in zip(selector.ranking_,feature_names,selector.support_):print(i)

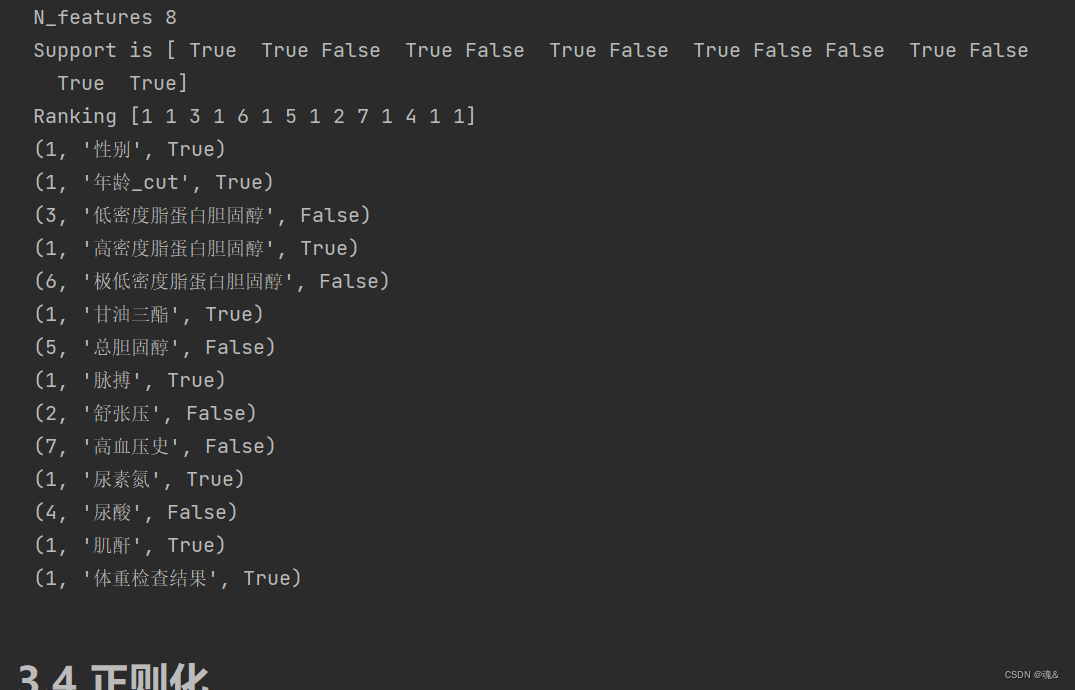
在这里插入图片描述

正则化法
正则化其实也可以叫规范化，举个例子

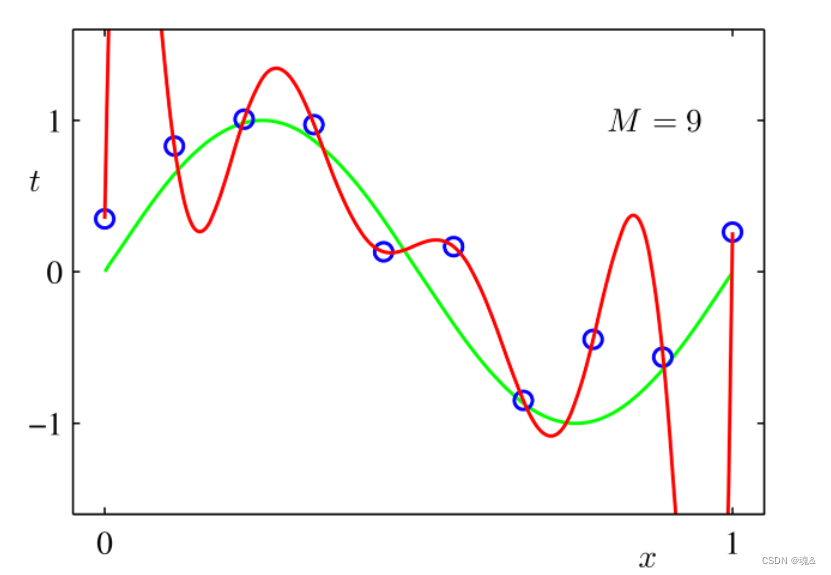
正则化就是增加一些限制条件，让红线曲线变得规范，从而变成绿线，以此达到过拟合的目的

model = LinearSVC(penalty= 'l1', C = 0.1,dual=False)
model.fit(X,y)
# 特征选择
# L1惩罚项的SVC作为基模型的特征选择,也可以使用threshold（权值系数之差的阈值）控制选择特征的个数
selector = SelectFromModel(estimator = model, prefit=True,max_features=8)
X_new = selector.transform(X)
feature_names = np.array(X.columns)
feature_names[selector.get_support()]#获取选择的变量

在这里插入图片描述

五、模型训练与评价

这里我才用混淆矩阵中的精确率(TP/(TP+FP))和召回率(TP/(TP+FN))、精确率和召回率的加权平均数(F1-score)、以及ROC曲线中的AUC(曲线下方面积占整个图的面积的比例)来对模型进行评估。其中ROC曲线是以假正率(FP/(FP+TN))为X轴，召回率为Y轴。
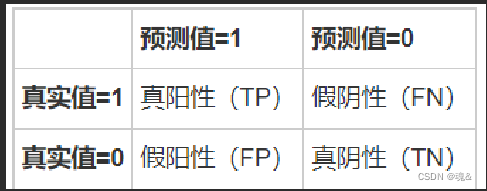
在这里插入图片描述

5.1 准备工作

select_features=[ '年龄_cut','高密度脂蛋白胆固醇','舒张压','脉搏','尿素氮','体重检查结果',"性别","甘油三酯"]
X1 = dataConcat[select_features]#变量筛选后的特征
y1 = dataConcat.是否糖尿病
# 切分数据集
train_X, val_X, train_y, val_y = train_test_split(X1, y1, random_state=1)

5.2 逻辑回归

select_features=[ '年龄_cut','高密度脂蛋白胆固醇','舒张压','脉搏','尿素氮','体重检查结果',"性别","甘油三酯"]
X1 = dataConcat[select_features]#变量筛选后的特征
y1 = dataConcat.是否糖尿病
# 切分数据集
train_X, val_X, train_y, val_y = train_test_split(X1, y1, random_state=1)model_logistics = LogisticRegression()
model_logistics.fit(train_X,train_y)
y_pred = model_logistics.predict(val_X)scores_logistics=[]
scores_logistics.append(precision_score(val_y, y_pred))
scores_logistics.append(recall_score(val_y, y_pred))confusion_matrix_logistics=confusion_matrix(val_y,y_pred)f1_score_logistics=f1_score(val_y, y_pred,labels=None, pos_label=1, average='binary', sample_weight=None)precision_logistics = precision_score(val_y, y_pred, average='binary')# 精确率指模型预测为正的样本中实际也为正的样本占被预测为正的样本的比例。importance=pd.DataFrame({"columns":list(val_X.columns), "coef":list(model_logistics.coef_.T)})predictions_log=model_logistics.predict_proba(val_X)#每一类的概率FPR_log, recall_log, thresholds = roc_curve(val_y, predictions_log[:,1],pos_label=1)area_log=auc(FPR_log,recall_log)print('logistics模型结果：\n')
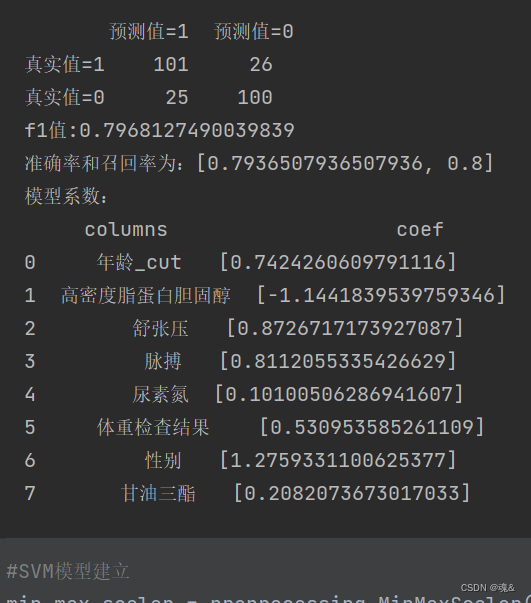
print(pd.DataFrame(columns=['预测值=1','预测值=0'],index=['真实值=1','真实值=0'],data=confusion_matrix_logistics))#混淆矩阵
print("f1值:"+str(f1_score_logistics))
print("准确率和召回率为："+str(scores_logistics))
print('模型系数：\n'+str(importance))

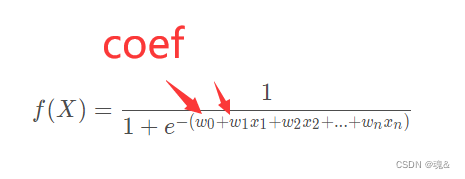
在这里插入图片描述

5.3 SVM

min_max_scaler = preprocessing.MinMaxScaler()#注意要归一化X_train_minmax = min_max_scaler.fit_transform(train_X)
X_test_minmax=min_max_scaler.transform(val_X)
model_svm=SVC(probability=True)
model_svm.fit(X_train_minmax,train_y)
y_pred = model_svm.predict(X_test_minmax)
scores_svm=[]
scores_svm.append(precision_score(val_y, y_pred))
scores_svm.append(recall_score(val_y, y_pred))
confusion_matrix_svm=confusion_matrix(val_y,y_pred)
f1_score_svm=f1_score(val_y, y_pred,labels=None, pos_label=1, average='binary', sample_weight=None)
predictions_svm=model_svm.predict_proba(X_test_minmax)#每一类的概率
FPR_svm, recall_svm, thresholds = roc_curve(val_y,predictions_svm[:,1], pos_label=1)
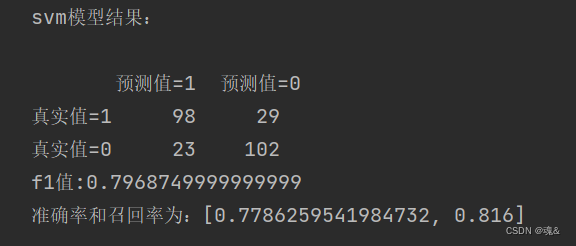
area_svm = auc(FPR_svm,recall_svm)print('svm模型结果：\n')
print(pd.DataFrame(columns=['预测值=1','预测值=0'],index=['真实值=1','真实值=0'],data=confusion_matrix_svm))#混淆矩阵
print("f1值:"+str(f1_score_svm))
print("准确率和召回率为："+str(scores_svm))

在这里插入图片描述
5.3 xgboost

model_XGB = XGBClassifier()
eval_set = [(val_X, val_y)]
model_XGB.fit(train_X, train_y, early_stopping_rounds=500, eval_metric="logloss", eval_set=eval_set, verbose=False)
# verbose改为True就能可视化loss
y_pred = model_XGB.predict(val_X)scores_XGB=[]
scores_XGB.append(precision_score(val_y, y_pred))
scores_XGB.append(recall_score(val_y, y_pred))
confusion_matrix_XGB=confusion_matrix(val_y,y_pred)
f1_score_XGB=f1_score(val_y, y_pred,labels=None, pos_label=0, average="binary", sample_weight=None)predictions_xgb=model_XGB.predict_proba(val_X)#每一类的概率
FPR_xgb, recall_xgb, thresholds = roc_curve(val_y,predictions_xgb[:,1], pos_label=1)
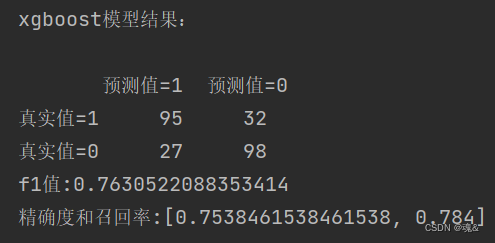
area_xgb = auc(FPR_xgb,recall_xgb)print('xgboost模型结果：\n')
print(pd.DataFrame(columns=['预测值=1','预测值=0'],index=['真实值=1','真实值=0'],data=confusion_matrix_XGB))#混淆矩阵
print("f1值:"+str(f1_score_XGB))
print("精确度和召回率:"+str(scores_XGB))

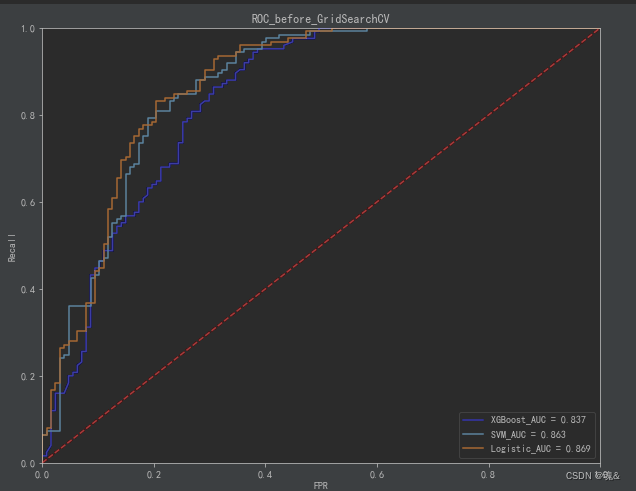
在这里插入图片描述
5.4 绘制ROC曲线

plt.figure(figsize=(10,8))
plt.plot(FPR_xgb, recall_xgb, 'b', label='XGBoost_AUC = %0.3f' % area_xgb)
plt.plot(FPR_svm, recall_svm,label='SVM_AUC = %0.3f' % area_svm)
plt.plot(FPR_log, recall_log,label='Logistic_AUC = %0.3f' % area_log)
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],'r--')
plt.xlim([0.0,1.0])
plt.ylim([0.0,1.0])
plt.ylabel('Recall')
plt.xlabel('FPR')
plt.title('ROC_before_GridSearchCV')
plt.show()

在这里插入图片描述

六、模型优化

以下都采用网格搜索交叉验证(GridSearchCV)的方式来寻找最佳参数

6.1 Logistic模型调优： C：C为正则化系数λ的倒数，必须为正数，默认为1。值越小，代表正则化越强。

parameters_Logr = {'C':[0.05,0.1,0.5,1]}
grid_search_log = GridSearchCV(model_logistics,parameters_Logr, cv=5,scoring='roc_auc')
grid_search_log.fit(train_X, train_y)
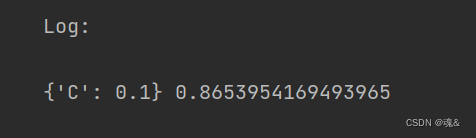
print('Log:\n')
print(grid_search_log.best_params_,grid_search_log.best_score_)

在这里插入图片描述

6.2 SVM模型调优： C：惩罚系数，即对误差的宽容度。c越高，说明越不能容忍出现误差,容易过拟合。C越小，容易欠拟合。C过大或过小，泛化能力变差 gamma：选择RBF函数作为kernel后，该函数自带的一个参数。隐含地决定了数据映射到新的特征空间后的分布，gamma越大，支持向量越少，gamma值越小，支持向量越多。支持向量的个数影响训练与预测的速度。

parameters_svm = {'C':[0.05,0.1,1,5,10,20,50,100],'gamma':[0.01,0.05,0.1,0.2,0.3]}
grid_search_svm = GridSearchCV(model_svm,parameters_svm, cv=5,scoring='roc_auc')
grid_search_svm.fit(X_train_minmax, train_y)
print('\nSVM:\n')
print(grid_search_svm.best_params_,grid_search_svm.best_score_)

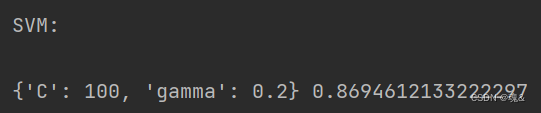
在这里插入图片描述

6.3 XGBoost参数调优： XGBoost的参数较多，这里三个参数进行了调整，共分为两步调整。整体思路是先调整较为重要的一组参数，然后将调到最优的参数输入模型后继续调下一组参数。

#第一步：先调max_depth、min_child_weight
param_test1 = {'max_depth':range(3,10,2),'min_child_weight':range(1,6,2)
}
gsearch1 = GridSearchCV(estimator = XGBClassifier(),param_grid = param_test1,scoring='roc_auc')
gsearch1.fit(train_X,train_y,early_stopping_rounds=500, eval_metric="logloss", eval_set=eval_set, verbose=False)
gsearch1.best_params_,gsearch1.best_score_

在这里插入图片描述

在#第二步：调gamma
param_test2 = {'gamma':[0.01,0.05,0.1,0.2,0.3,0.5,1]
}
gsearch2 = GridSearchCV(estimator = XGBClassifier(max_depth=3,min_child_weight=3),param_grid = param_test2, scoring='roc_auc', cv=5)
gsearch2.fit(train_X,train_y,early_stopping_rounds=500, eval_metric="logloss", eval_set=eval_set, verbose=False)
gsearch2.best_params_, gsearch2.best_score_

在这里插入图片描述

七、与原模型进行对比

7.1 logistics

model_logistics_after = LogisticRegression(C=0.5)
model_logistics_after.fit(train_X,train_y)
y_pred_after = model_logistics_after.predict(val_X)
scores_logistics_after=[]
scores_logistics_after.append(precision_score(val_y, y_pred_after))
scores_logistics_after.append(recall_score(val_y, y_pred_after))
confusion_matrix_logistics_after=confusion_matrix(val_y,y_pred_after)
f1_score_logistics_after=f1_score(val_y, y_pred_after,labels=None, pos_label=1, average='binary', sample_weight=None)
precision_logistics_after = precision_score(val_y, y_pred_after, average='binary')# 精确率指模型预测为正的样本中实际也为正的样本占被预测为正的样本的比例。
importance_after=pd.DataFrame({"columns":list(val_X.columns), "coef":list(model_logistics_after.coef_.T)})
predictions_log_after=model_logistics_after.predict_proba(val_X)#每一类的概率
FPR_log_after, recall_log_after, thresholds_after = roc_curve(val_y, predictions_log_after[:,1],pos_label=1)
area_log_after=auc(FPR_log_after,recall_log_after)print('调参后logistics模型结果：\n')
print(pd.DataFrame(columns=['预测值=1','预测值=0'],index=['真实值=1','真实值=0'],data=confusion_matrix_logistics_after))#混淆矩阵
print("f1值:"+str(f1_score_logistics_after))
print("准确率和召回率为："+str(scores_logistics_after))
print('模型系数：\n'+str(importance_after))

在这里插入图片描述

7.2 SVM

#SVM模型建立
min_max_scaler = preprocessing.MinMaxScaler()#注意要归一化
X_train_minmax = min_max_scaler.fit_transform(train_X)
X_test_minmax=min_max_scaler.transform(val_X)
model_svm=SVC(probability=True)
model_svm.fit(X_train_minmax,train_y)
y_pred = model_svm.predict(X_test_minmax)
scores_svm=[]
scores_svm.append(precision_score(val_y, y_pred))
scores_svm.append(recall_score(val_y, y_pred))
confusion_matrix_svm=confusion_matrix(val_y,y_pred)
f1_score_svm=f1_score(val_y, y_pred,labels=None, pos_label=1, average='binary', sample_weight=None)
predictions_svm=model_svm.predict_proba(X_test_minmax)#每一类的概率
FPR_svm, recall_svm, thresholds = roc_curve(val_y,predictions_svm[:,1], pos_label=1)
area_svm = auc(FPR_svm,recall_svm)print('svm模型结果：\n')
print(pd.DataFrame(columns=['预测值=1','预测值=0'],index=['真实值=1','真实值=0'],data=confusion_matrix_svm))#混淆矩阵
print("f1值:"+str(f1_score_svm))
print("准确率和召回率为："+str(scores_svm))

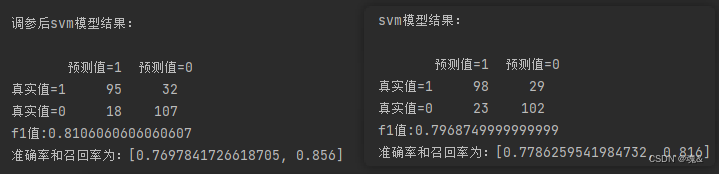
在这里插入图片描述

7.3 xgboost

model_XGB_after = XGBClassifier(max_depth= 3, min_child_weight= 3,gamma=0.5)
eval_set = [(val_X, val_y)]
model_XGB_after.fit(train_X, train_y, early_stopping_rounds=500, eval_metric="logloss", eval_set=eval_set, verbose=False)
# verbose改为True就能可视化loss
y_pred_after = model_XGB_after.predict(val_X)scores_XGB_after=[]
scores_XGB_after.append(precision_score(val_y, y_pred_after))
scores_XGB_after.append(recall_score(val_y, y_pred_after))
confusion_matrix_XGB_after=confusion_matrix(val_y,y_pred_after)
f1_score_XGB_after=f1_score(val_y, y_pred_after,labels=None, pos_label=0, average="binary", sample_weight=None)predictions_xgb_after=model_XGB_after.predict_proba(val_X)#每一类的概率
FPR_xgb_after, recall_xgb_after, thresholds_after = roc_curve(val_y,predictions_xgb_after[:,1], pos_label=1)
area_xgb_after = auc(FPR_xgb_after,recall_xgb_after)print('调参后xgboost模型结果：\n')
print(pd.DataFrame(columns=['预测值=1','预测值=0'],index=['真实值=1','真实值=0'],data=confusion_matrix_XGB_after))#混淆矩阵
print("f1值:"+str(f1_score_XGB_after))
print("精确度和召回率:"+str(scores_XGB_after))

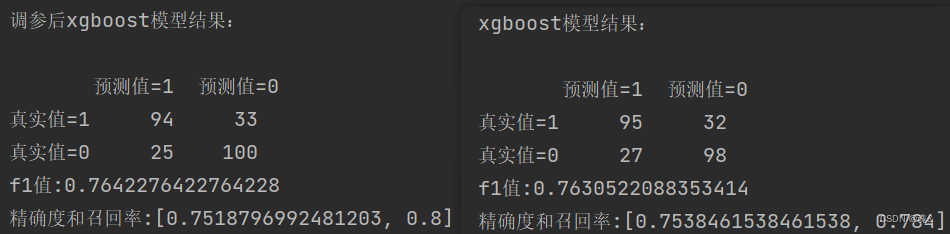
在这里插入图片描述

7.4 ROC曲线绘制

plt.figure(figsize=(10,8))
plt.plot(FPR_xgb_after, recall_xgb_after, 'b', label='XGBoost_AUC = %0.3f' % area_xgb_after)
plt.plot(FPR_svm_after, recall_svm_after,label='SVM_AUC = %0.3f' % area_svm_after)
plt.plot(FPR_log_after, recall_log_after,label='Logistic_AUC = %0.3f' % area_log_after)
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],'r--')
plt.xlim([0.0,1.0])
plt.ylim([0.0,1.0])
plt.ylabel('Recall')
plt.xlabel('FPR')
plt.title('ROC_after_GridSearchCV')
plt.show()

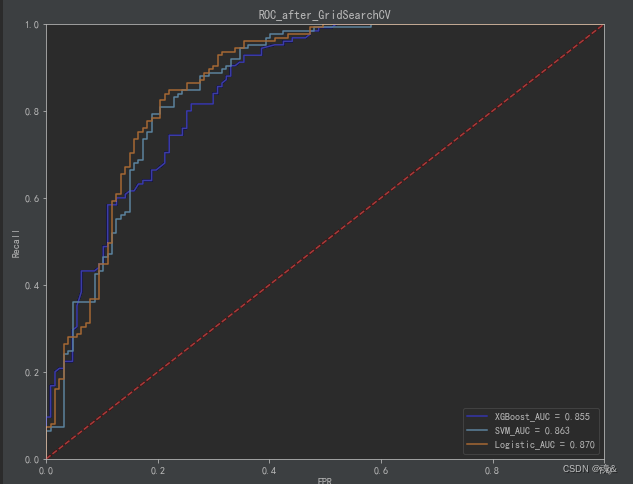
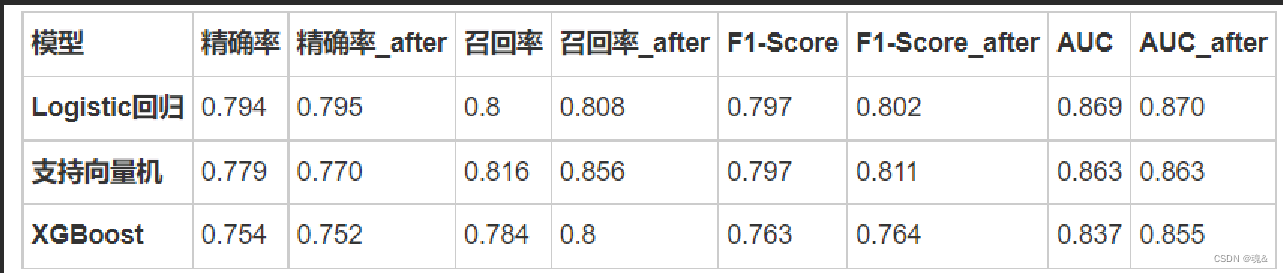
在这里插入图片描述

7.5总体对比
从对比结果可以看出，调参后的模型性能总体略优于调参前的模型。总之，机器学习模型调参是一个需要细致和耐心的工作，不断的努力可能只能带来性能的微小提升

八、作业总结

此次作业以体检数据集为样本进行了机器学习的预测，但是需要注意几个问题：
体检数据量太少，仅有1006条可分析数据，这对于糖尿病预测来说是远远不足的，所分析的结果代表性不强。这里的数据糖尿病和正常人基本相当，而真实的数据具有很强的不平衡性。也就是说，糖尿病患者要远少于正常人，这种不平衡的数据集给真实情况下糖尿病的预测带来了很大困难，当然可以通过上采样、下采样或者其他方法进行不平衡数据集的预测。缺少时序数据使得预测变得不准确，时序数据更能够体现一个人的身体状态。总而言之，机器学习预测疾病道阻且长，尽信机器学习不如无机器学习，经验加技术才是医学预测未来发展的大方向。