leetcode 扫描线专题 06-leetcode.836 rectangle-overlap 力扣.836 矩形重叠

题目

矩形以列表 [x1, y1, x2, y2] 的形式表示，其中 (x1, y1) 为左下角的坐标，(x2, y2) 是右上角的坐标。

矩形的上下边平行于 x 轴，左右边平行于 y 轴。

如果相交的面积为正，则称两矩形重叠。

需要明确的是，只在角或边接触的两个矩形不构成重叠。

给出两个矩形 rec1 和 rec2。如果它们重叠，返回 true；否则，返回 false 。

示例 1：

输入：rec1 = [0,0,2,2], rec2 = [1,1,3,3]
输出：true

示例 2：

输入：rec1 = [0,0,1,1], rec2 = [1,0,2,1]
输出：false

示例 3：

输入：rec1 = [0,0,1,1], rec2 = [2,2,3,3]
输出：false

提示：

rect1.length == 4

rect2.length == 4

-10^9 <= rec1[i], rec2[i] <= 10^9

rec1 和 rec2 表示一个面积不为零的有效矩形

小结

感觉有一个顺序的问题。

应该先学习一下 T836 + T223 + T850 可能再做这一题就会比较自然。

v1-投影

思路

判断两个矩形是否重叠的通用条件是通过其投影区间是否有交集：

两矩形沿 x 轴投影有重叠，且两矩形沿 y 轴投影有重叠。

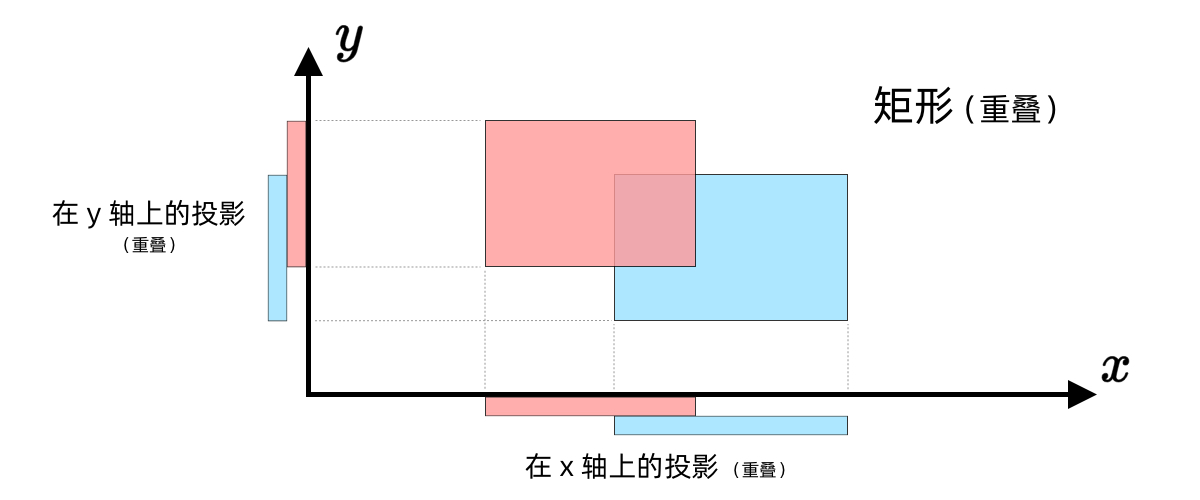
矩形投影到坐标轴上，就变成了区间。稍加思考，我们发现：两个互相重叠的矩形，它们在 x 轴和 y 轴上投影出的区间也是互相重叠的。这样，我们就将矩形重叠问题转化成了区间重叠问题。

区间重叠是一维的问题，比二维问题简单很多。

我们可以穷举出两个区间所有可能的 6 种关系：

可以看到，区间的 6 种关系中，不重叠只有两种情况，判断不重叠更简单。

假设两个区间分别是 [s1, e1] 和 [s2, e2] 的话，区间不重叠的两种情况就是 e1 <= s2 和 e2 <= s1。

公式化为：

x 轴投影相交：rec1[2] > rec2[0] && rec1[0] < rec2[2] y 轴投影相交：rec1[3] > rec2[1] && rec1[1] < rec2[3]

解法

class Solution {public boolean isRectangleOverlap(int[] rec1, int[] rec2) {// 判断 x 轴和 y 轴投影是否有交集boolean xOverlap = rec1[2] > rec2[0] && rec1[0] < rec2[2];boolean yOverlap = rec1[3] > rec2[1] && rec1[1] < rec2[3];// 两个投影都有交集才算重叠return xOverlap && yOverlap;}
}

小结

投影这种解法看起来很简单，实际上很巧妙，但是有时候我们不见得能想到。

v2-重叠面积

思路

如果两个矩形重叠，那么重叠的面积一定大于0.

于是问题变成如何计算重叠的矩形面积？

如果有重叠，重叠的部分也一定是一个矩形

交集面积的计算方式是基于两个矩形的重叠区域的 左下角和右上角的坐标 来推算的。

具体来说，两个矩形的交集矩形（如果存在）也是一个矩形，它的边界由两个矩形的边界决定。

计算重叠面积

第一个矩形 rec1 = [x1, y1, x2, y2]，表示其左下角坐标为 (x1, y1)，右上角坐标为 (x2, y2)。
第二个矩形 rec2 = [x3, y3, x4, y4]，表示其左下角坐标为 (x3, y3)，右上角坐标为 (x4, y4)。

如果两个矩形有交集，那么交集的矩形的左下角和右上角的坐标可以通过取两者的最大和最小值来确定：

交集矩形的左下角：(x1', y1') = (max(x1, x3), max(y1, y3))
交集矩形的右上角：(x2', y2') = (min(x2, x4), min(y2, y4))

判断交集是否存在

交集矩形的面积只有在其宽度和高度都大于 0 时才存在。

如果交集矩形的宽度或高度小于等于 0，说明两个矩形没有交集。

因此，交集矩形的宽度和高度的计算方式如下：

宽度：width = x2' - x1'
高度：height = y2' - y1'

交集矩形的面积则为：

面积 = width * height，但是如果宽度或高度小于等于 0，面积就为 0。

因此，计算交集的面积时，我们需要确保 width > 0 和 height > 0，否则交集的面积为 0。

代码示例

public class Solution {public boolean isRectangleOverlap(int[] rec1, int[] rec2) {// 计算交集矩形的左下角和右上角int x1 = Math.max(rec1[0], rec2[0]);int y1 = Math.max(rec1[1], rec2[1]);int x2 = Math.min(rec1[2], rec2[2]);int y2 = Math.min(rec1[3], rec2[3]);// 计算交集的宽度和高度int width = x2 - x1;int height = y2 - y1;// 如果交集的宽度和高度都大于 0，说明有重叠if (width > 0 && height > 0) {return true;}// 没有重叠return false;}
}

效果

0ms 100%

小结

这个感觉比方法 1 的投影应该更容易想到一些。

而且可以在后续的 T223 T3047 中拓展使用。

v3-扫描线

扫描线

使用扫描线（sweepline）方法解决这个问题也是一种非常常见且高效的方式。

扫描线的基本思路是将矩形视为一系列的线段，并在 x 轴方向上依次“扫描”这些线段，检查是否有重叠。

思路

将矩形的边界转换为事件：
- 每个矩形有 两条边，一个是左边界（x1），一个是右边界（x2）。这两条边界构成了扫描线的“事件”。
- 对于每个矩形，生成两个事件：
  - 左边界事件：表示矩形开始时，增加一个 y 区间（从 y1 到 y2）。
  - 右边界事件：表示矩形结束时，移除一个 y 区间（从 y1 到 y2）。
事件排序：
- 所有的事件按 x 坐标排序。如果 x 坐标相同，优先处理右边界事件（因为在同一位置时，应该先移除结束的矩形，再处理新的开始）。
扫描线处理：
- 扫描线从左到右扫描这些事件。当扫描到一个 左边界事件 时，添加相应的 y 区间；当扫描到一个 右边界事件 时，移除相应的 y 区间。
- 在每次添加或移除事件时，检查当前的 y 区间是否存在重叠。如果存在重叠，那么矩形就重叠。
区间重叠检查：
- 在扫描线过程中，维护一个 活动的 y 区间集合，该集合记录了当前所有矩形在 y 轴上的区间。
- 每次添加新的 y 区间时，检查当前 y 区间是否与已经存在的区间重叠。如果重叠，则说明存在矩形重叠。

详细步骤

定义事件：
- 每个矩形 rec = [x1, y1, x2, y2] 会生成两个事件：
  - 左边界事件 (x1, y1, y2, 1) 表示矩形开始（1 表示是左边界）。
  - 右边界事件 (x2, y1, y2, -1) 表示矩形结束（-1 表示是右边界）。
排序事件：
- 按照 x 坐标排序，如果两个事件的 x 坐标相同，右边界事件优先。

为什么要这样做？

因为在扫描线的过程中，当我们遇到同一个 x 坐标时，我们希望先处理右边界事件，再处理左边界事件。

这是为了避免在处理过程中出现误判的情况。

比如，当一个矩形的右边界和另一个矩形的左边界在同一个 x 坐标上时，我们应该先“移除”第一个矩形的 y 区间，然后再“添加”第二个矩形的 y 区间。

扫描并更新活动区间：
- 用一个数据结构（比如 TreeSet）维护当前的活动区间。每次扫描到一个事件时，更新该区间，检查是否存在重叠。

如何判断是否重叠：

private boolean hasOverlap(TreeSet<int[]> activeIntervals) {int prevEnd = Integer.MIN_VALUE;  // 初始化 prevEnd 为一个极小值for (int[] interval : activeIntervals) {// 如果当前区间的起始点小于前一个区间的终点，说明有重叠if (interval[0] < prevEnd) {return true;  // 有重叠，返回 true}prevEnd = interval[1];  // 更新 prevEnd 为当前区间的终点}return false;  // 如果没有任何重叠，返回 false
}

实现

import java.util.*;public class Solution {public boolean isRectangleOverlap(int[] rec1, int[] rec2) {// 如果 rec1 和 rec2 的 x 范围没有交集，直接返回 falseif (rec1[2] <= rec2[0] || rec1[0] >= rec2[2]) {return false;}// 生成事件列表List<int[]> events = new ArrayList<>();// 对 rec1 和 rec2 的边界生成事件// 左边界事件 [x, y1, y2, type]，type = 1 表示左边界，-1 表示右边界events.add(new int[]{rec1[0], rec1[1], rec1[3], 1});  // rec1 左边界events.add(new int[]{rec1[2], rec1[1], rec1[3], -1}); // rec1 右边界events.add(new int[]{rec2[0], rec2[1], rec2[3], 1});  // rec2 左边界events.add(new int[]{rec2[2], rec2[1], rec2[3], -1}); // rec2 右边界// 按 x 坐标排序，x 相同的话，优先处理右边界事件events.sort((a, b) -> a[0] == b[0] ? b[3] - a[3] : a[0] - b[0]);// 活动区间维护TreeSet<int[]> activeIntervals = new TreeSet<>((a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);for (int[] event : events) {int x = event[0];int y1 = event[1];int y2 = event[2];int type = event[3];if (type == 1) { // 左边界事件，加入活动区间activeIntervals.add(new int[]{y1, y2});} else { // 右边界事件，移除活动区间activeIntervals.remove(new int[]{y1, y2});}// 检查活动区间是否有重叠if (hasOverlap(activeIntervals)) {return true;}}return false;}// 检查活动区间是否有重叠private boolean hasOverlap(TreeSet<int[]> activeIntervals) {int prevEnd = Integer.MIN_VALUE;for (int[] interval : activeIntervals) {if (interval[0] < prevEnd) {return true;  // 有重叠}prevEnd = interval[1]; // 更新 prevEnd}return false;  // 没有重叠}
}