240.搜索二维矩阵 II
编写一个高效的算法来搜索
m x n矩阵matrix中的一个目标值target。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
先动手写写最简单方法,二重循环。
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int m=matrix.size(),n=matrix[0].size();if(m==0||n==0) return{};for(auto& itx:matrix){for(auto& itxy:itx){if(itxy==target) return true;}}return false;}
};优化方法的话,根据昨天做的题,感觉大多数矩阵相关的题目都是依靠找规律,那我们再看看例图:

以“5”这一项为例,左边和上边的数比 5 小,右边和下边的数比 5 大。可以利用这一特点,从左下角或者右上角开始顺藤摸瓜。
以从右上角为例,如果target小于15,就向左移一位,如果target大于15,就向右移一位,以此类推,如果已经移出了矩阵的边界,说明没找到target的值,就返回false。
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int m=matrix.size(),n=matrix[0].size();if(m==0||n==0) return{};int x=0,y=n-1;while(x<=m-1&&y>=0){if(matrix[x][y]==target) return true;else if(matrix[x][y]>target){y--;}else{x++;}}return false;}
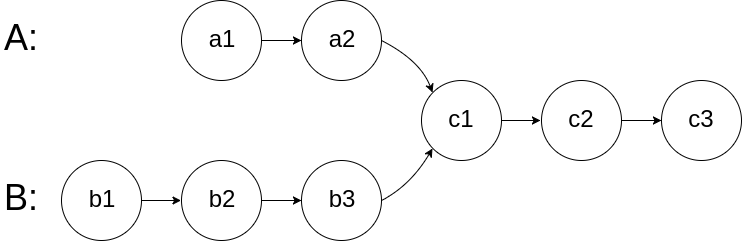
};160. 相交链表
给你两个单链表的头节点
headA和headB,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回null。图示两个链表在节点
c1开始相交:
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
自定义评测:
评测系统 的输入如下(你设计的程序 不适用 此输入):
intersectVal- 相交的起始节点的值。如果不存在相交节点,这一值为0listA- 第一个链表listB- 第二个链表skipA- 在listA中(从头节点开始)跳到交叉节点的节点数skipB- 在listB中(从头节点开始)跳到交叉节点的节点数评测系统将根据这些输入创建链式数据结构,并将两个头节点
headA和headB传递给你的程序。如果程序能够正确返回相交节点,那么你的解决方案将被 视作正确答案 。
虽然是简单题但其实是最让我痛苦的一道。!看一眼题目感觉还好理解,一看给的例子就懵了。

好了这种情况下先不要急,看一下方法体吧。输入是两个链表的头结点,输出的是相交节点。那目的先可以初步确定了。
一开始看到可能会没什么思路,这是正常的,因为题目对相交链表的表述不太清楚。这道题中相交链表的定义是一个从某一结点开始,两链表相交后,后面的结点完全相同。
验证一下它说的是不是这样,我添加了一个用例,在中间的某一位置相交,又在后面分开:


可见确实如此,糟老头子坏得很啊。
这样的话,两个链表相交的过程就可以简化成下面这样了👇
| a1->a2->...->ai | ->c1->c2->...->cn |
| b1->b2->...->bj |
设想一下,如果 1~i 和 1~j 的值相同就好了,那就意味着这两个链表长度相同,A和B链表上的指针到达相交结点的时间是相同的。
但事实是两个链表不一定长度相同,不过思路还是一样,是不是只要A和B两个链表的指针同时到达相交结点,就可以找到这个结点了?
我们现在已知,遍历A链表需要指针移动(i+n)次,遍历B链表需要指针移动(j+n)次,不如让A链表的指针遍历完A后再遍历一遍B链表,并且B链表指针遍历完B后再遍历A链表,这样的话,每一个指针都一共要移动(i+j+2n)次,那么第一个找到的满足(pa==pb)的结点,就一定是相交结点。
如果两个链表没有重合也不用担心,两个指针会在链表的尾部相遇,然后返回一个空指针。
这样就可以写出代码:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {if(headA==nullptr||headB==nullptr) return nullptr;ListNode *pa=headB,*pb=headA;while(pa!=pb){if(pa) pa=pa->next;else pa=headB;if(pb) pb=pb->next;else pb=headA;}return pa;}
};但再具体想一想,如果两链表后面的结点不一样,只有中间连续的1~n的结点相交的情况下,这个方法能不能用呢?答案是不能!因为相交结点后面的长度会影响到指针到达相交节点。比如说链表A如果是(i1+n+i2),链表B是(j1+n+j2),那用之前的两个都遍历的方法,A的指针pa第二次到达相交结点走过的路程是(i1+n+i2+j1),而链表B第二次到达相交结点走过的路程是(j1+n+j2+i1)!!!
206. 反转链表
给你单链表的头节点
head,请你反转链表,并返回反转后的链表。
反转无非是把 a1 -> a2 -> a3 ->..._> an -> nullptr 改成 nullptr <- a1 <- a2 <-...<- an。
比如遍历用的指针是p,我们把p的next改成前驱结点就好了。不过前驱结点需要提前记录,而且为了在改变了p->next之后还可以继续遍历,就需要先把后继p->next存下来再改成前驱即可。所以整理一下,对结点的调整步骤为:
1. 保存后继
2. 把next改成前驱结点
3. 把当前结点改成前驱
4. 让p移向下一个结点
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* reverseList(ListNode* head) {if(!head) return nullptr;ListNode* p=head;ListNode* pre=nullptr;while(p!=nullptr){ListNode* next=p->next;p->next=pre;pre=p;p=next;}return pre;}
};234. 回文链表
给你一个单链表的头节点
head,请你判断该链表是否为回文链表。如果是,返回true;否则,返回false。
克服恐惧的最好方法就是避免恐惧(。。),不会操作链表但是向想写出来,就先把它复制进数组里再对它使用双指针!过了就是胜利✌
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:bool isPalindrome(ListNode* head) {vector<int> nums;while(head!=nullptr){nums.emplace_back(head->val);head=head->next;}int left=0,right=nums.size()-1;while(left<right){if(nums[left]==nums[right]){left++;right--;}else{return false;}}return true;}
};说笑了,下面看看正规方法来做。
我们刚刚既然已经写过了反转链表,那这一次不如用上。
直接在它给的链表上改,把前一半链表都反转,后一半链表不变,然后用两个指针分别遍历前后两段,一边遍历一边比较。
如何实现只反转一半?怎么找到链表的中点?这里可以使用快慢指针,快指针一次进两格,慢指针一次进一格,那么当fast或者fast->next为空时,slow所在的位置就是中点了。
不过要注意,当结点数为奇数时,我们需要用中点后面那个点作为后半部分的起始点。
如何判断链表是奇数个还是偶数个?在纸上画一下,以题目提供的测试用例为例:

fast经历的结点索引值是0,2,“4”。所以当结点是偶数个时,fast==nullptr,以此类推,当结点为奇数个时,fast->next=nullptr。
梳理一下目前我们用到的变量,快慢指针是肯定的,fast用来确定奇偶和中点,slow摸到中点顺便用于反转链表,pre是反转用到的前驱结点,next是反转用到的后继结点。
当摸到中点并且完成反转时,我们的链表变成了这样👇(以4个和5个结点的链表为例)
a1 <- a2 a3 -> a4 -> a5 【pre在a2的位置,slow在a3的位置,next在a4的位置,fast在a5的位置】
a1 <- a2 a3 -> a4 【pre在a2的位置,slow在a3的位置,next在a4的位置,fast在a4后面的位置】
因此,偶数个结点的话用pre和slow来遍历一下链表就行了,奇数个结点的话就把slow处理一下再遍历。
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:bool isPalindrome(ListNode* head) {if(head==nullptr||head->next==nullptr) return true;ListNode* slow=head;ListNode* fast=head;ListNode* pre=nullptr;ListNode* next=nullptr;//快指针在链表尾部,慢指针在中点while(fast&&fast->next){fast=fast->next->next;next=slow->next;slow->next=pre;pre=slow;slow=next;}//fast为空是偶数,fast不为空是奇数if(fast!=nullptr){slow=slow->next;}//利用pre和slow比较是否相等while(slow!=nullptr&&pre!=nullptr){if(slow->val!=pre->val){return false;}slow=slow->next;pre=pre->next;}return true;}
};这题下次还是用复制进数组的方法吧(。。。。)