实验原理
有理函数z 变换的部分分式展开
【实例2-1】试用Matlab 命令对函数 X ( z ) = 18 18 + 3 − 1 − 4 z − 2 − z − 3 X\left(z\right)=\frac{18}{18+3^{-1} -4z^{-2} -z^{-3} } X(z)=18+3−1−4z−2−z−318 进行部分分式展开,并求出其z 反变换。
B=[18];
A=[18 3 -4 -1];
[R,P,k]=residuez(B,A)
R = 3x1 0.36000.24000.4000P = 3x1 0.5000-0.3333-0.3333k =[]
从运行结果可知, p 2 = p 3 p_2 =p_3 p2=p3 ,表示系统有一个二重极点。所以, X ( z ) X(z) X(z) 的部分分式展开为:
X ( z ) = 0.36 1 − 0.5 z − 1 + 0.24 1 + 0.3333 z − 1 + 0.4 ( 1 + 0.3333 z − 1 ) 2 X\left(z\right)=\frac{0.36}{1-0.5z^{-1} }+\frac{0.24}{1+0.3333z^{-1} }+\frac{0.4}{{\left(1+0.3333z^{-1} \right)}^2 } X(z)=1−0.5z−10.36+1+0.3333z−10.24+(1+0.3333z−1)20.4
系统函数的零极点分析
【实例2-2】已知一离散因果LTI 系统的系统函数为
H ( z ) = z + 0.32 z 2 + z + 0.16 H\left(z\right)=\frac{z+0.32}{z^2 +z+0.16} H(z)=z2+z+0.16z+0.32
试用Matlab 命令求该系统的零极点。
clear;
B=[1,0.32];
A=[1,1,0.16];
[R,P,K]=tf2zp(B,A)
R = -0.3200
P = 2x1 -0.8000-0.2000K = 1
因此,零点为 z = 0.32 z=0.32 z=0.32 ,极点为 p 1 = 0.8 p_1 =0.8 p1=0.8 与 p 2 = 0.2 p_2 =0.2 p2=0.2 。
若要获得系统函数 H(z) 的零极点分布图,可直接应用 zplane 函数,其语句格式为
zplane ( B , A ) \textrm{zplane}(B,A) zplane(B,A)
其中,B 与 A 分别表示 H(z) 的分子和分母多项式的系数向量。它的作用是在 Z平面上画出单位圆、零点与极点。
【实例2-3】已知一离散因果LTI 系统的系统函数为
H ( z ) = z 2 − 0.36 z 2 − 1.52 z + 0.68 H\left(z\right)=\frac{z^2 -0.36}{z^2 -1.52z+0.68} H(z)=z2−1.52z+0.68z2−0.36
试用Matlab 命令绘出该系统的零极点分布图。
B=[1 -0.36];
A=[1 -1.52 0.68];
zplane(B,A),grid on
legend('零点','极点')
title('零极点分布图')
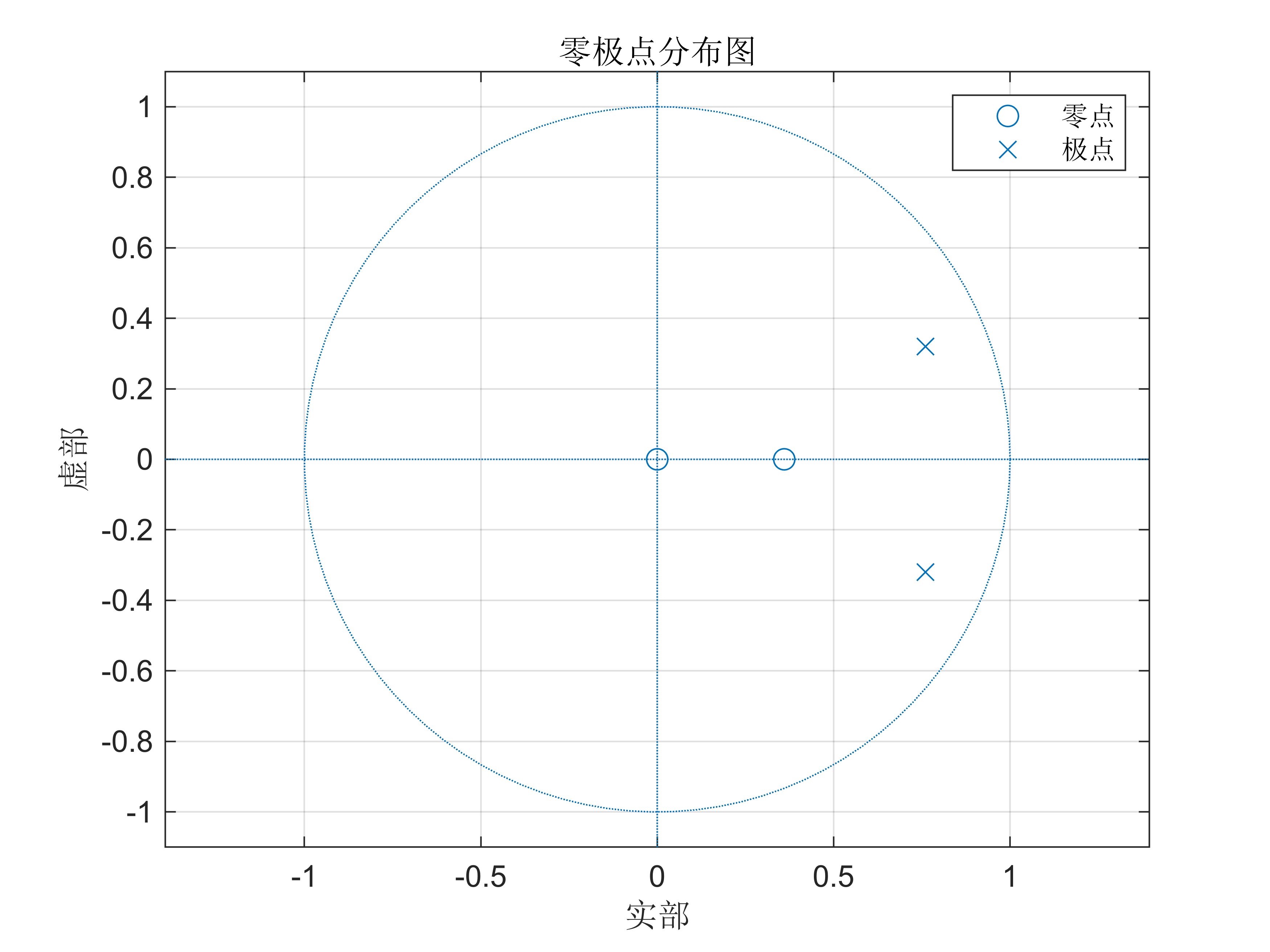
程序运行结果如图所示。可见,该因果系统的极点全部在单位圆内,故系统是稳定的。
【实例2-4】试用MATLAB 命令画出现下列系统函数的零极点分布图、以及对应
的时域单位取样响应 h(n)的波形,并分析系统函数的极点对时域波形的影响。
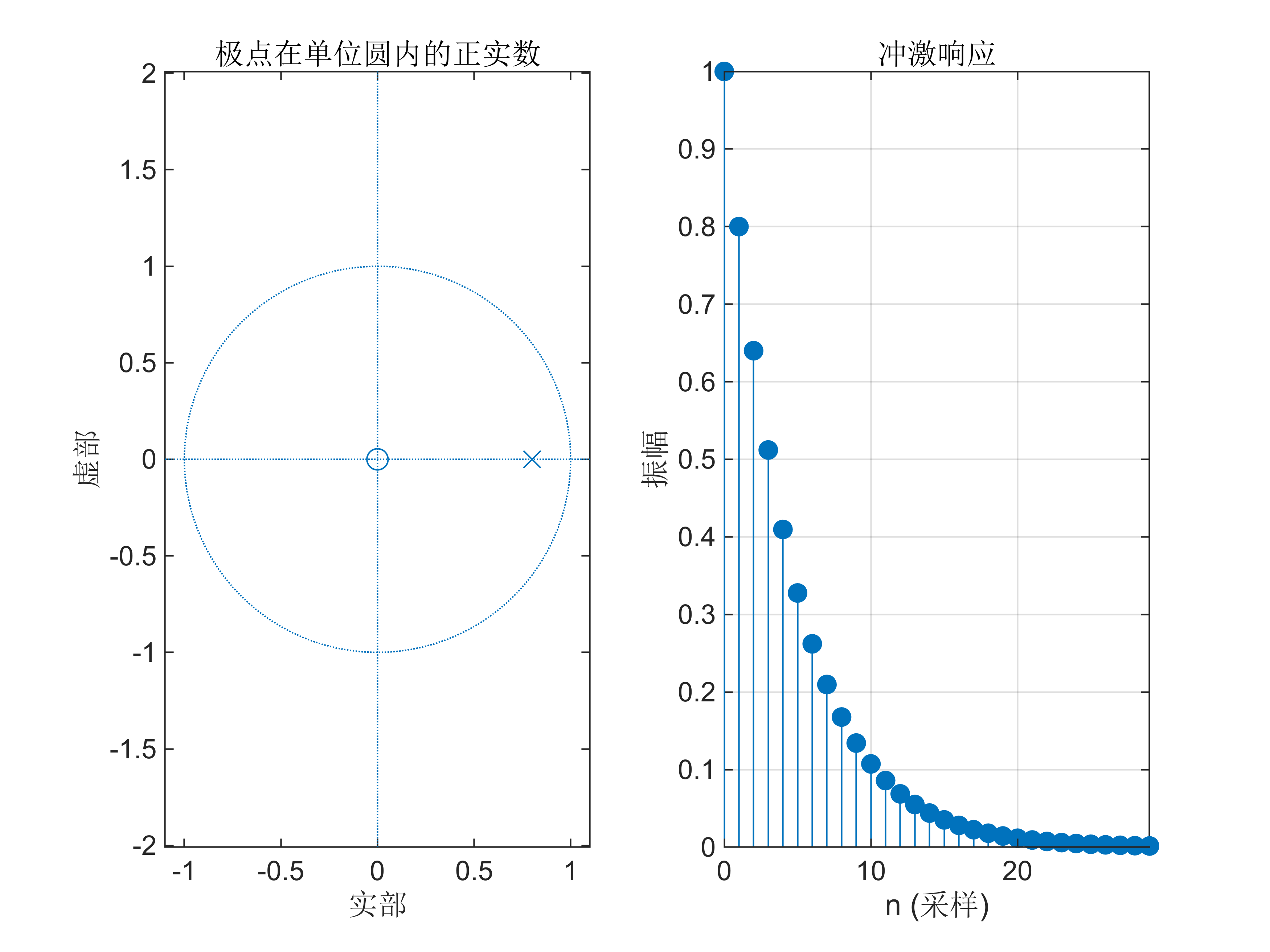
1. H 1 ( z ) = z z − 0.8 2. H 2 ( z ) = z z + 0.8 3. H 3 ( z ) = z z 2 − 1.2 z + 0.72 4. H 4 ( z ) = z z − 1 5. H 5 ( z ) = z z 2 − 1.6 z + 1 6. H 6 ( s ) = z z − 1.2 7. H 7 ( z ) = z z 2 − 2 z + 1.36 \begin{array}{l} 1.\newline {H_1 (z)=\frac{z}{z-0.8}}\textrm{ 2.}\;{H_2 (z)=\frac{z}{z+0.8}}\textrm{ 3.}\;{H_3 (z)=\frac{z}{z^2 -1.2z+0.72}}\textrm{ 4.}\;{H_4 (z)=\frac{z}{z-1}}\textrm{ 5.}\;{H_5 (z)=\frac{z}{z^2 -1.6z+1}}\textrm{ 6.}\;{H_6 (s)=\frac{z}{z-1.2}}\textrm{ 7.}\;{H_7 (z)=\frac{z}{z^2 -2z+1.36}}\textrm{ }\newline \end{array} 1.H1(z)=z−0.8z 2.H2(z)=z+0.8z 3.H3(z)=z2−1.2z+0.72z 4.H4(z)=z−1z 5.H5(z)=z2−1.6z+1z 6.H6(s)=z−1.2z 7.H7(z)=z2−2z+1.36z
clear;
% 定义分子和分母系数
b1 = [1, 0];
a1 = [1, -0.8];% 绘制零极点图
subplot(121); % 分割绘图窗口为1行2列,并在第1个位置绘图
zplane(b1, a1); % 绘制零极点图
title('极点在单位圆内的正实数'); % 设置标题% 绘制单位脉冲响应
subplot(122); % 在第2个位置绘图
impz(b1, a1, 30); % 绘制单位脉冲响应,采样点数为30
grid on; % 显示网格
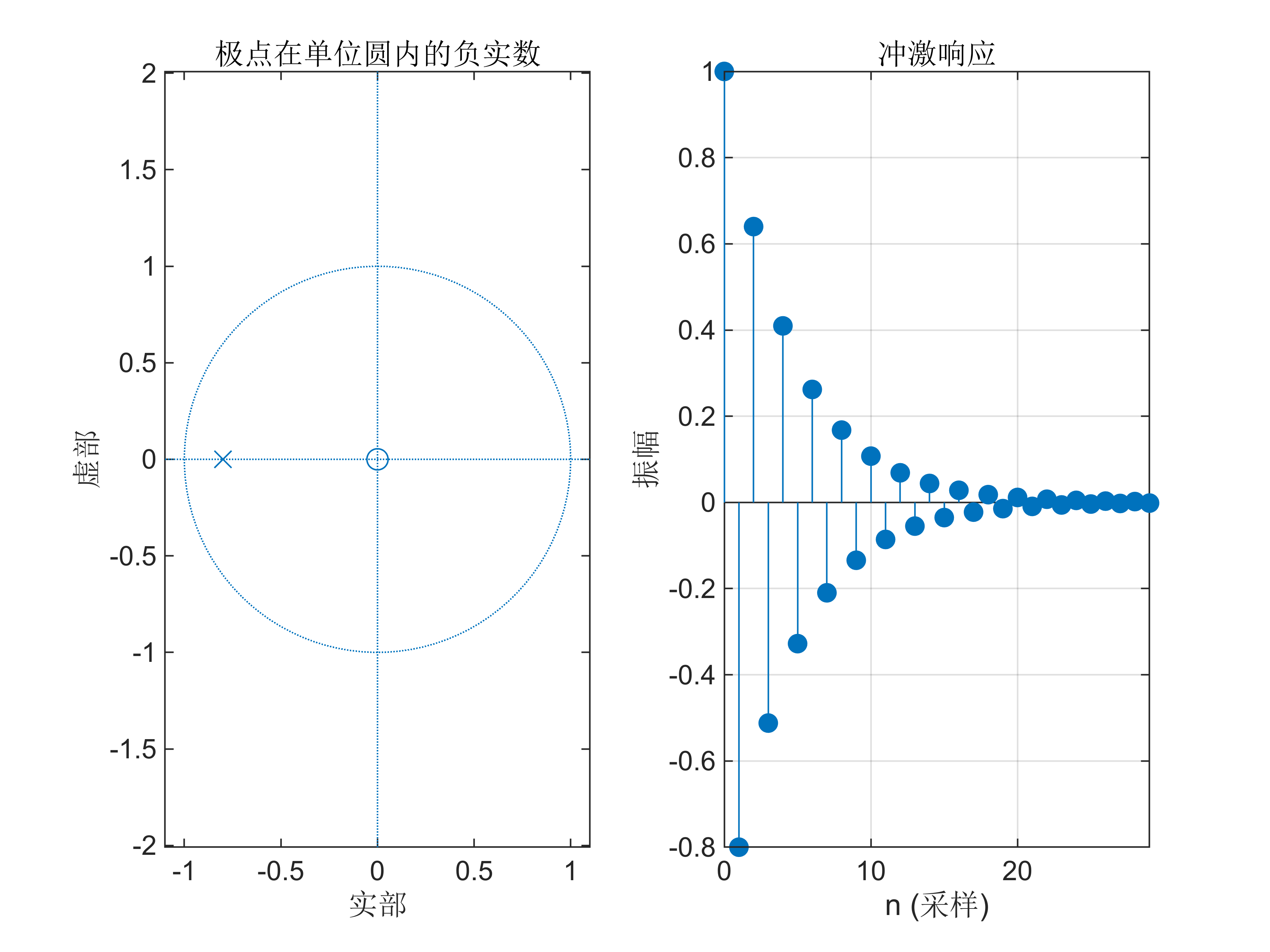
% 定义新的分子和分母系数
b2 = [1, 0];
a2 = [1, 0.8];% 绘制零极点图
figure; % 新窗口
subplot(121); % 分割绘图窗口为1行2列,并在第1个位置绘图
zplane(b2, a2); % 绘制零极点图
title('极点在单位圆内的负实数'); % 设置标题% 绘制单位脉冲响应
subplot(122); % 在第2个位置绘图
impz(b2, a2, 30); % 绘制单位脉冲响应,采样点数为30
grid on; % 显示网格
% 定义新的分子和分母系数
b3 = [1, 0];
a3 = [1, -1.2, 0.72];% 绘制零极点图
figure; % 新窗口
subplot(121); % 分割绘图窗口为1行2列,并在第1个位置绘图
zplane(b3, a3); % 绘制零极点图
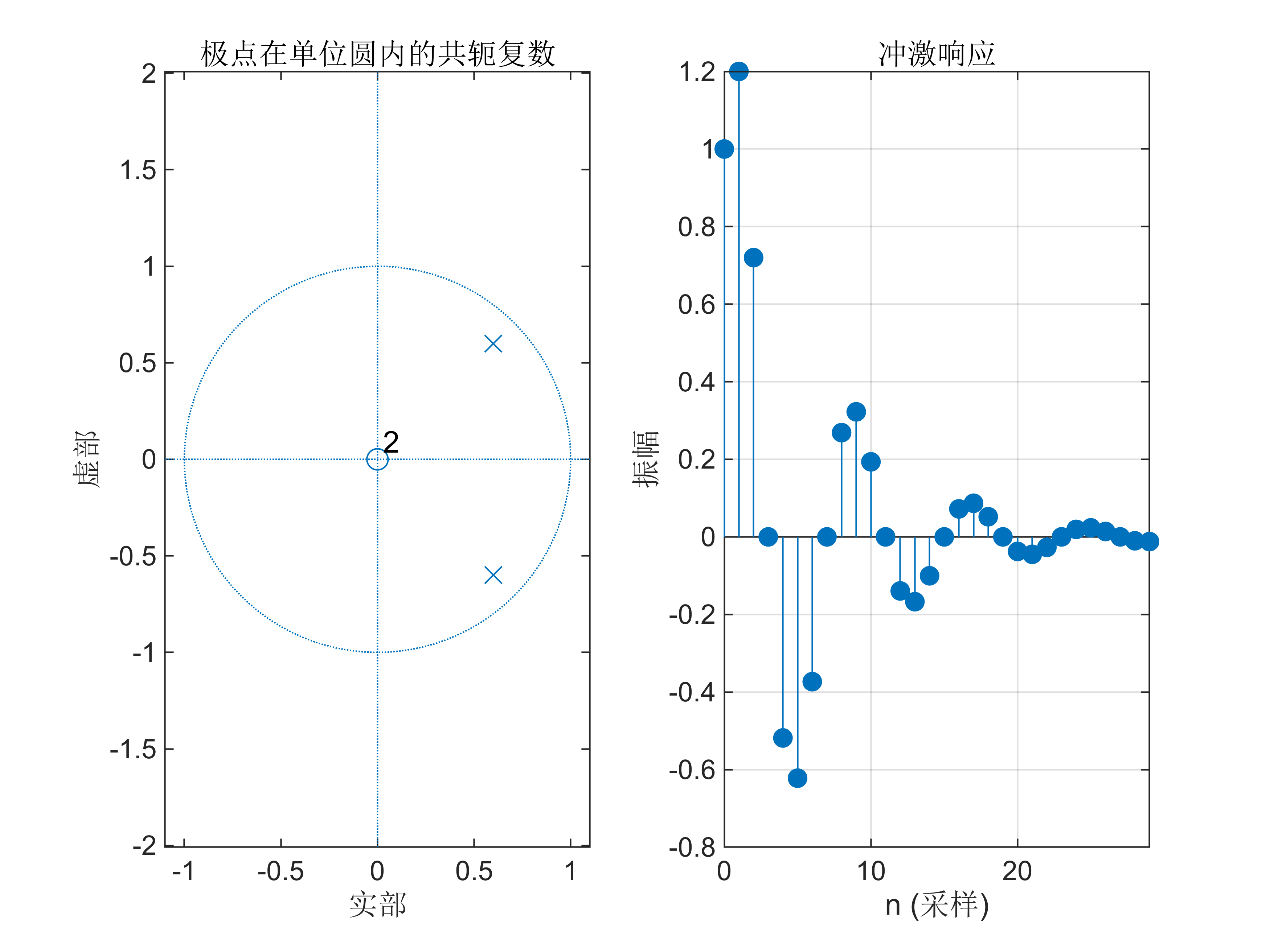
title('极点在单位圆内的共轭复数'); % 设置标题% 绘制单位脉冲响应
subplot(122); % 在第2个位置绘图
impz(b3, a3, 30); % 绘制单位脉冲响应,采样点数为30
grid on; % 显示网格
% 定义新的分子和分母系数
b4 = [1, 0];
a4 = [1, -1];% 绘制零极点图
figure; % 新窗口
subplot(121); % 分割绘图窗口为1行2列,并在第1个位置绘图
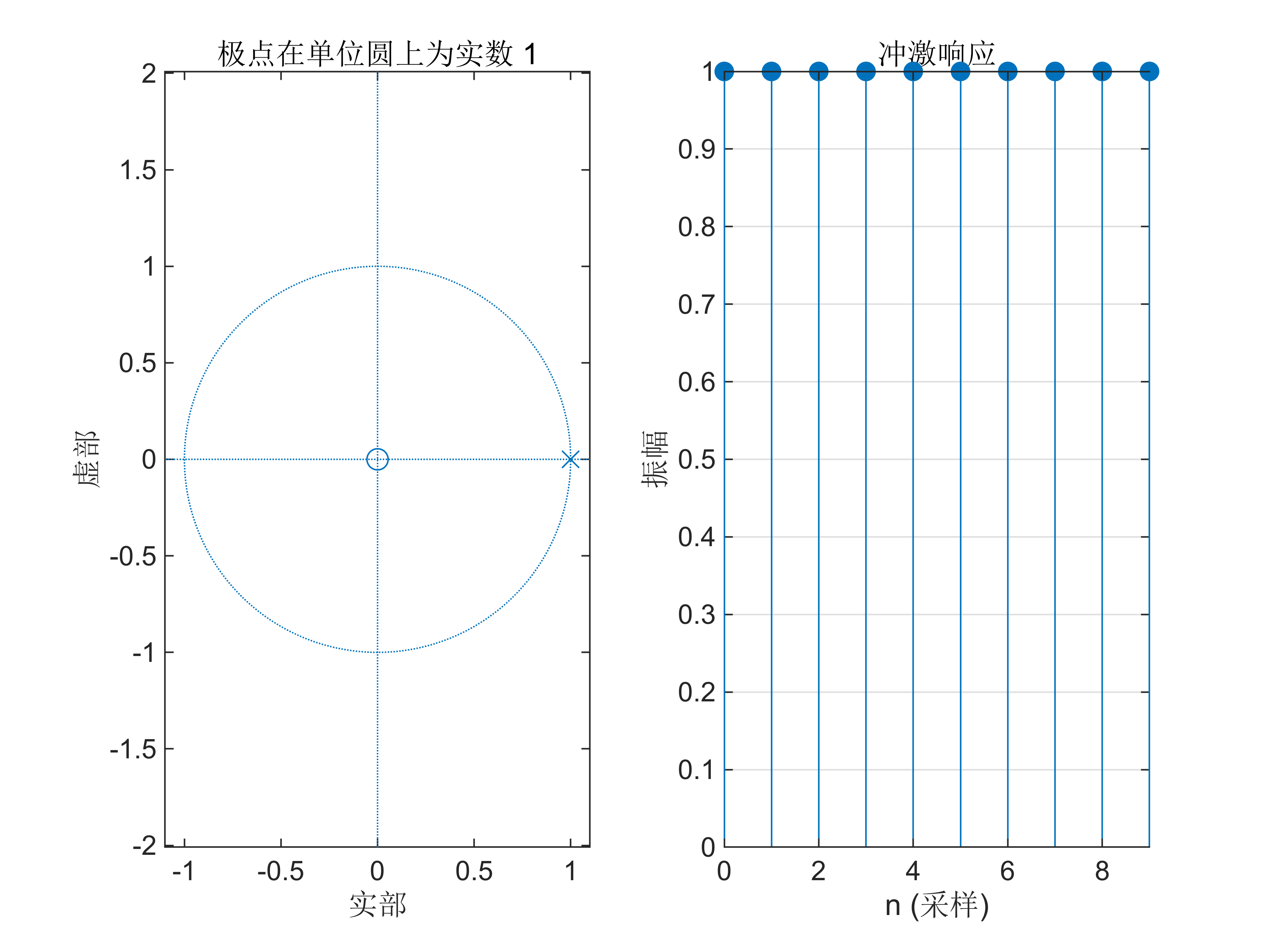
zplane(b4, a4); % 绘制零极点图
title('极点在单位圆上为实数 1'); % 设置标题% 绘制单位脉冲响应
subplot(122); % 在第2个位置绘图
impz(b4, a4); % 绘制单位脉冲响应
grid on; % 显示网格
% 定义新的分子和分母系数
b5 = [1, 0];
a5 = [1, -1.6, 1];% 绘制零极点图
figure; % 新窗口
subplot(121); % 分割绘图窗口为1行2列,并在第1个位置绘图
zplane(b5, a5); % 绘制零极点图
title('极点在单位圆上的共轭复数'); % 设置标题% 绘制单位脉冲响应
subplot(122); % 在第2个位置绘图
impz(b5, a5, 30); % 绘制单位脉冲响应,采样点数为30
grid on; % 显示网格% 定义新的分子和分母系数
b6 = [1, 0];
a6 = [1, -1.2];% 绘制零极点图
subplot(121); % 分割绘图窗口为1行2列,并在第1个位置绘图
zplane(b6, a6); % 绘制零极点图
title('极点在单位圆外的正实数'); % 设置标题% 绘制单位脉冲响应
subplot(122); % 在第2个位置绘图
impz(b6, a6, 30); % 绘制单位脉冲响应,采样点数为30
grid on; % 显示网格% 定义新的分子和分母系数
b7 = [1, 0];
a7 = [1, -2, 1.36];% 绘制零极点图
subplot(121); % 分割绘图窗口为1行2列,并在第1个位置绘图
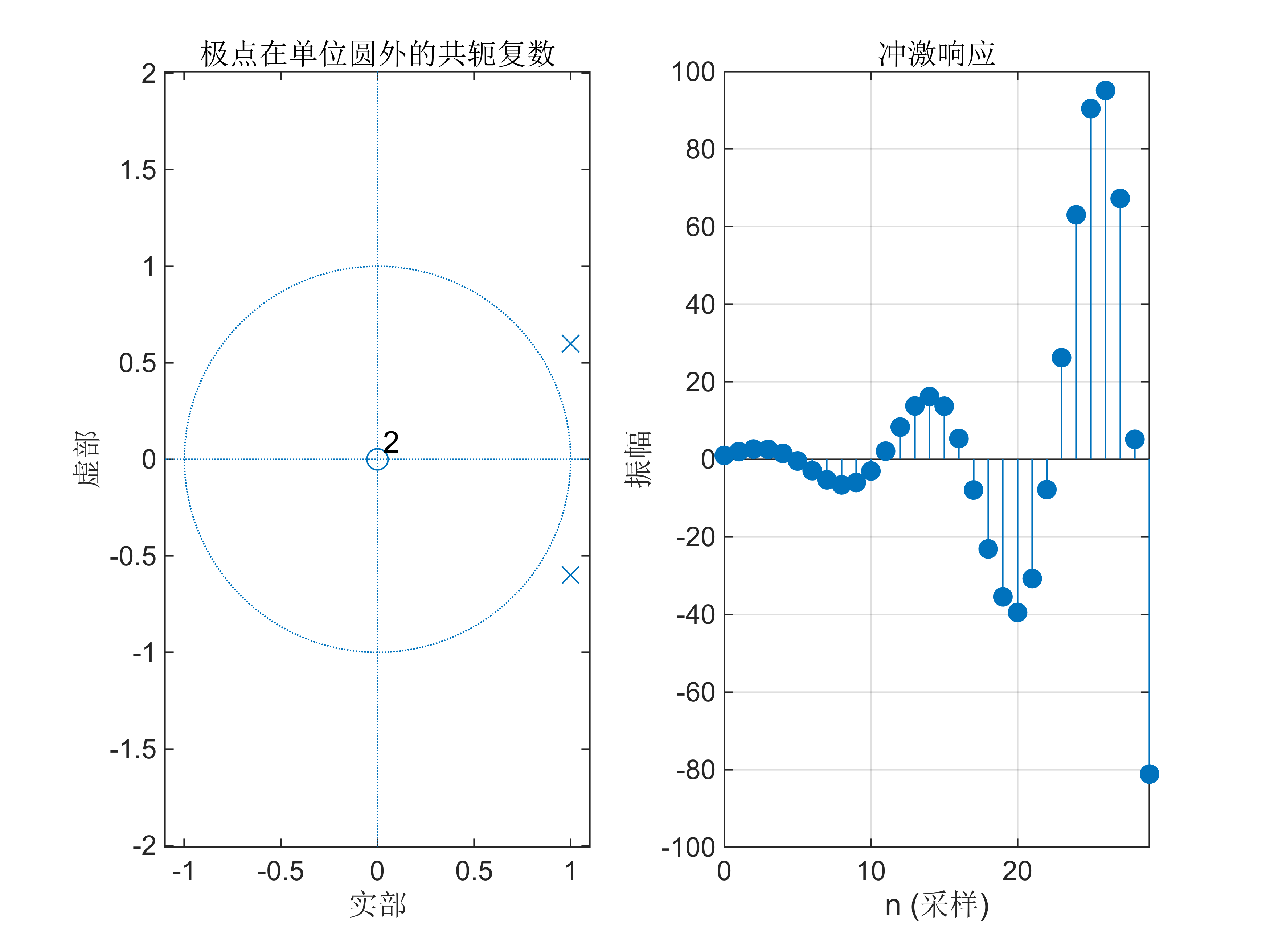
zplane(b7, a7); % 绘制零极点图
title('极点在单位圆外的共轭复数'); % 设置标题% 绘制单位脉冲响应
subplot(122); % 在第2个位置绘图
impz(b7, a7, 30); % 绘制单位脉冲响应,采样点数为30
grid on; % 显示网格
离散时间LTI 系统的频率特性分析
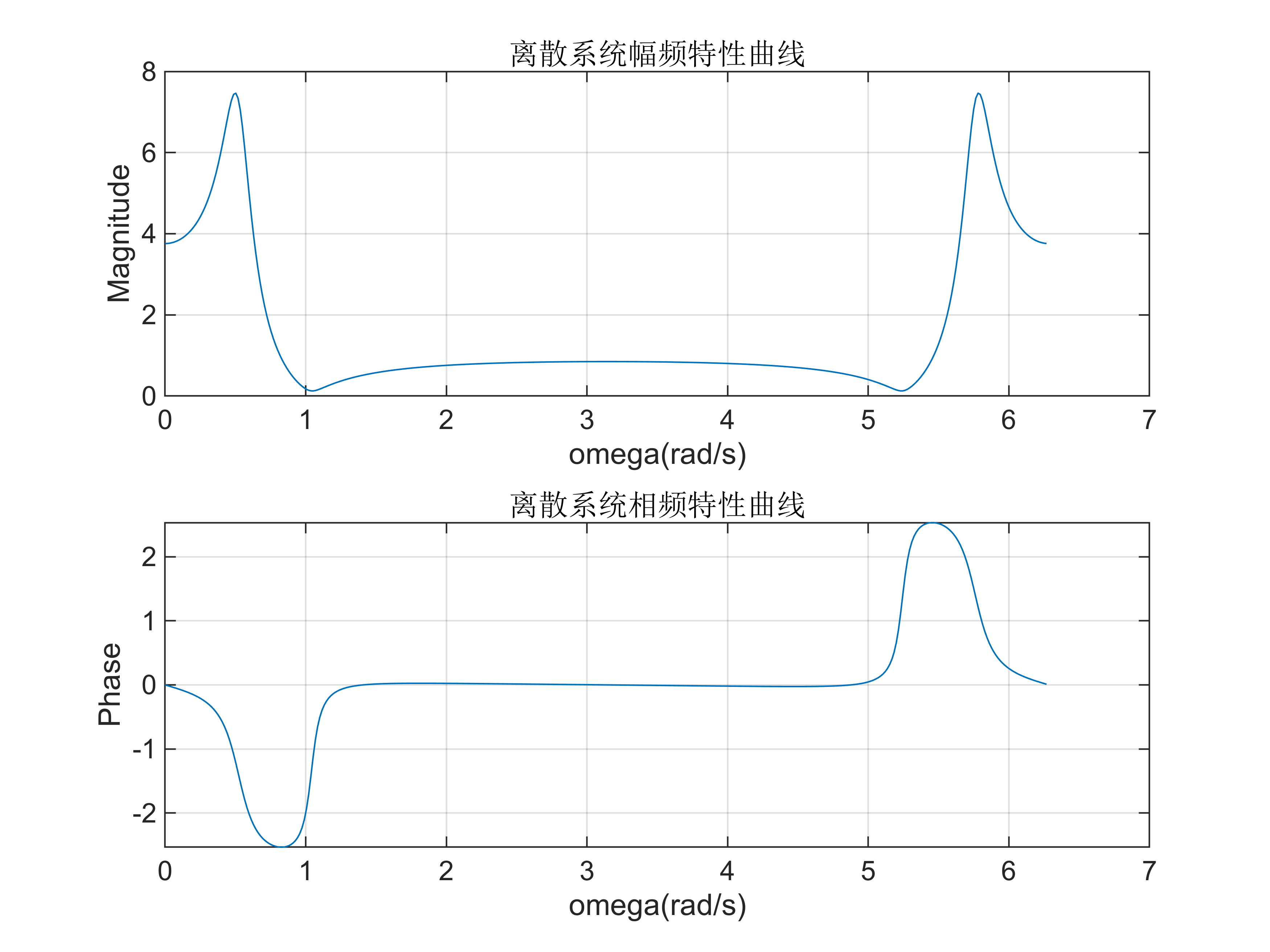
【实例2-5】用Matlab 命令绘制系统 H ( z ) = z 2 − 0.96 z + 0.9028 z 2 − 1.56 z + 0.8109 H\left(z\right)=\frac{z^2 -0.96z+0.9028}{z^2 -1.56z+0.8109} H(z)=z2−1.56z+0.8109z2−0.96z+0.9028 的频率响应曲线。
close;
clear;
% 定义分子和分母多项式的系数
b = [1 -0.96 0.9028];
a = [1 -1.56 0.8109];% 计算频率响应,使用400个点,覆盖整个频率范围[0, 2pi]
[H, w] = freqz(b, a, 400, 'whole');% 计算频率响应的幅值和相位
Hm = abs(H); % 幅值
Hp = angle(H); % 相位% 创建第一个子图,绘制幅频特性曲线
subplot(211); % 将图形窗口分割为2行1列,并在第1个位置绘图
plot(w, Hm); % 绘制幅值曲线
grid on; % 显示网格
xlabel("omega(rad/s)"); % x轴标签
ylabel('Magnitude'); % y轴标签
title('离散系统幅频特性曲线'); % 图形标题% 创建第二个子图,绘制相频特性曲线
subplot(212); % 在第2个位置绘图
plot(w, Hp); % 绘制相位曲线
grid on; % 显示网格
xlabel("omega(rad/s)"); % x轴标签
ylabel('Phase'); % y轴标签
title('离散系统相频特性曲线'); % 图形标题
实验内容
1.试用MATLAB 的residuez 函数,求出 H ( z ) = 2 z 4 + 16 z 3 + 44 z 2 + 56 z + 32 3 z 4 + 3 z 3 − 15 z 2 + 18 z − 12 H\left(z\right)=\frac{2z^4 +16z^3 +44z^2 +56z+32}{3z^4 +3z^3 -15z^2 +18z-12} H(z)=3z4+3z3−15z2+18z−122z4+16z3+44z2+56z+32 的部分分式展开和。
clear;
B=[2 16 44 56 32];
A=[3 3 -15 18 -12];
[R P K]=residuez(B,A)
R = 4x1 complex -0.0177 + 0.0000i9.4914 + 0.0000i-3.0702 + 2.3398i-3.0702 - 2.3398iP = 4x1 complex -3.2361 + 0.0000i
1.2361 + 0.0000i0.5000 + 0.8660i0.5000 - 0.8660iK = -2.6667
2. 试用Matlab 画出下列因果系统的系统函数零极点分布图,并判断系统的稳定性。
(1) H ( z ) = 2 z 2 − 1.6 z − 0.9 z 3 − 2.5 z 2 + 1.96 z − 0.48 (2) H ( z ) = z − 1 z 4 − 0.9 z 3 − 0.65 z 2 + 0.873 z \begin{array}{l} \textrm{(1)}H\left(z\right)=\frac{2z^2 -1.6z-0.9}{z^3 -2.5z^2 +1.96z-0.48}\newline \textrm{(2)}H\left(z\right)=\frac{z-1}{z^4 -0.9z^3 -0.65z^2 +0.873z} \end{array} (1)H(z)=z3−2.5z2+1.96z−0.482z2−1.6z−0.9(2)H(z)=z4−0.9z3−0.65z2+0.873zz−1
clear;
close;
b1=[2 -1.6 -0.9];
a1=[1 -2.5 1.96 -0.48];
% 绘制零极点图
figure;
subplot(121);
zplane(b1, a1);
title('极点在单位圆上的共轭复数'); % 绘制单位脉冲响应
subplot(122);
impz(b1, a1, 30); % 绘制单位脉冲响应,采样点数为30
grid on;
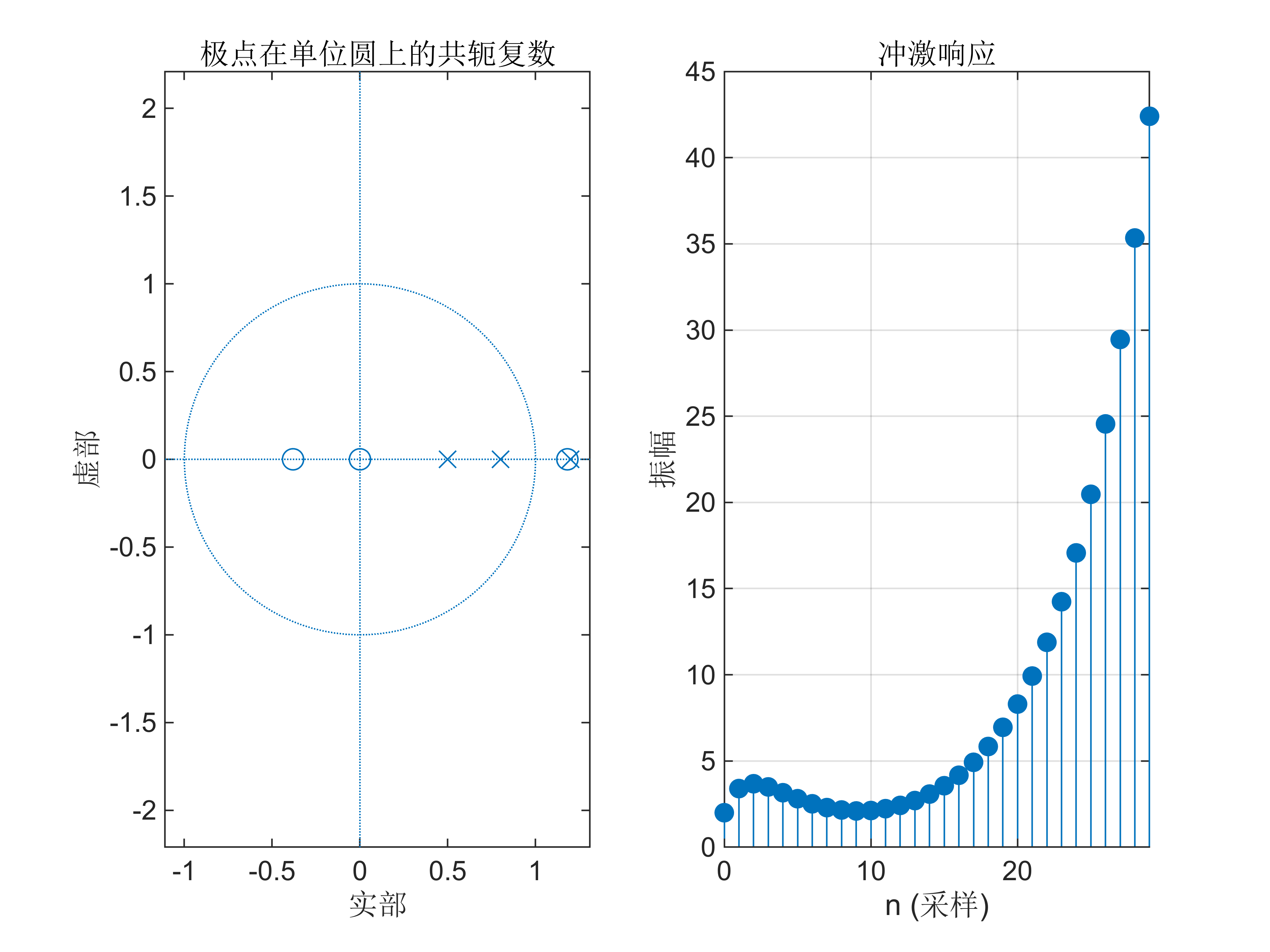
b2=[1 -1];
a2=[1 -0.9 -0.65 0.873];
% 绘制零极点图
figure;
subplot(121);
zplane(b2, a2);
title('极点在单位圆上的共轭复数'); % 绘制单位脉冲响应
subplot(122);
impz(b2, a2, 64); % 绘制单位脉冲响应,采样点数为64
grid on;
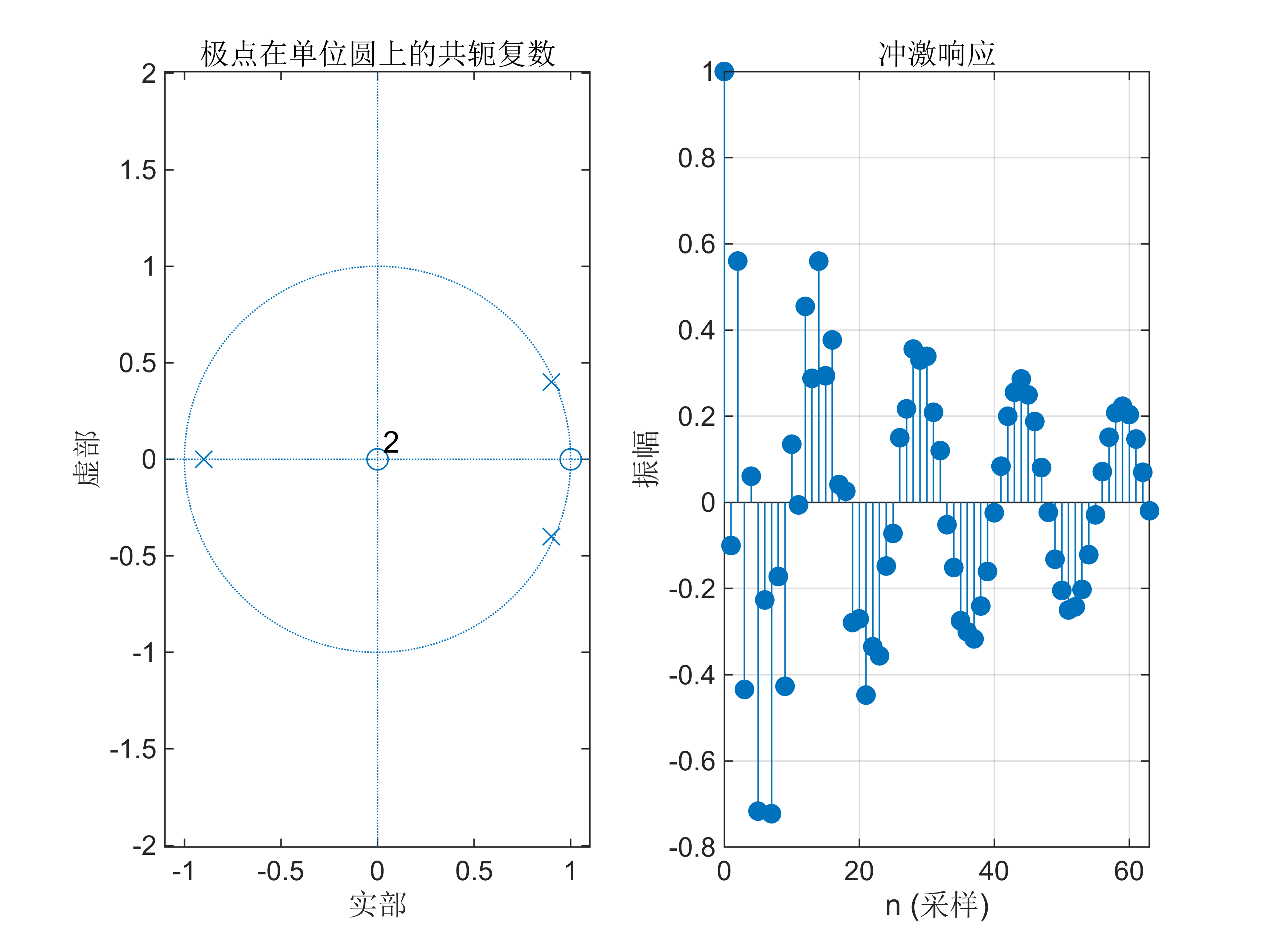
3. 试用Matlab 绘制系统 H ( z ) = z 2 z 2 − 3 4 z + 1 8 H\left(z\right)=\frac{z^2 }{z^2 -\frac{3}{4}z+\frac{1}{8}} H(z)=z2−43z+81z2 的频率响应曲线。
close;clear;
% 定义分子和分母多项式的系数
b = [1 0];
a = [1 -3/4 1/8];
% 计算频率响应,使用400个点,覆盖整个频率范围[0, 2pi]
[H, w] = freqz(b, a, 400, 'whole');
% 计算频率响应的幅值和相位
Hm = abs(H); % 幅值
Hp = angle(H); % 相位subplot(211);
plot(w, Hm); % 绘制幅值曲线
grid on;
xlabel("\omega(rad/s)");
ylabel('Magnitude');
title('离散系统幅频特性曲线'); subplot(212);
plot(w, Hp); % 绘制相位曲线
grid on;
xlabel("\omega(rad/s)");
ylabel('Phase');
title('离散系统相频特性曲线');
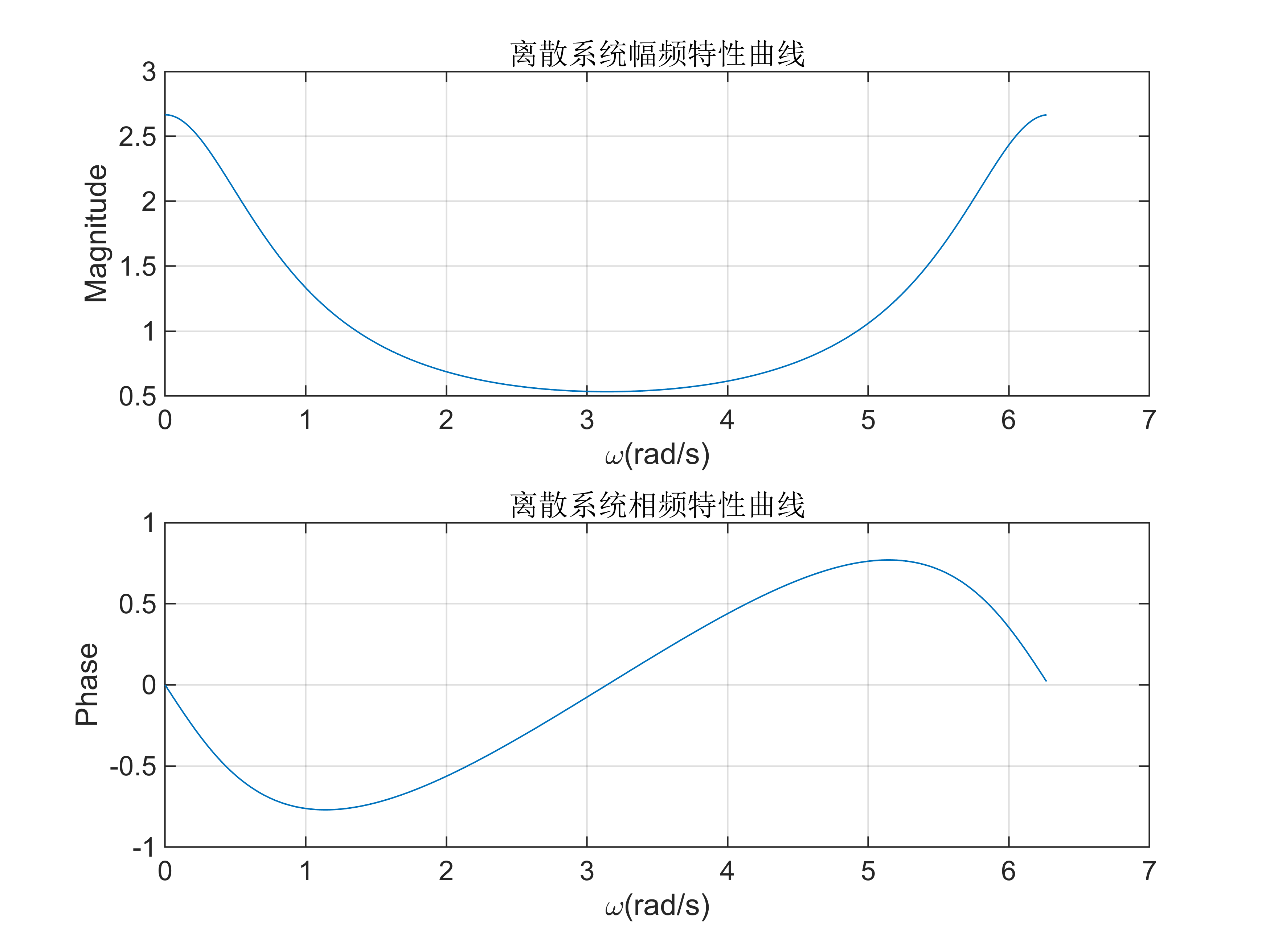
4. 编写Matlab 程序,系统的差分方程为 y ( n ) − 0.9 ( n − 8 ) = x ( n ) − x ( n − 8 ) y(n)-0.9(n-8)=x(n)-x(n-8) y(n)−0.9(n−8)=x(n)−x(n−8) 。
(1)画出该系统的零极点分布图,判断系统的稳定性;
(2)画出系统在0~2 π \pi π 范围内的幅频特性曲线和相频特性曲线;
(3)分析该系统是什么类型的滤波器。
clear;
close;
B=[1 0 0 0 0 0 0 0 -1];
A=[1 0 0 0 0 0 0 0 -0.9];
%% 问题1
zplane(B,A)
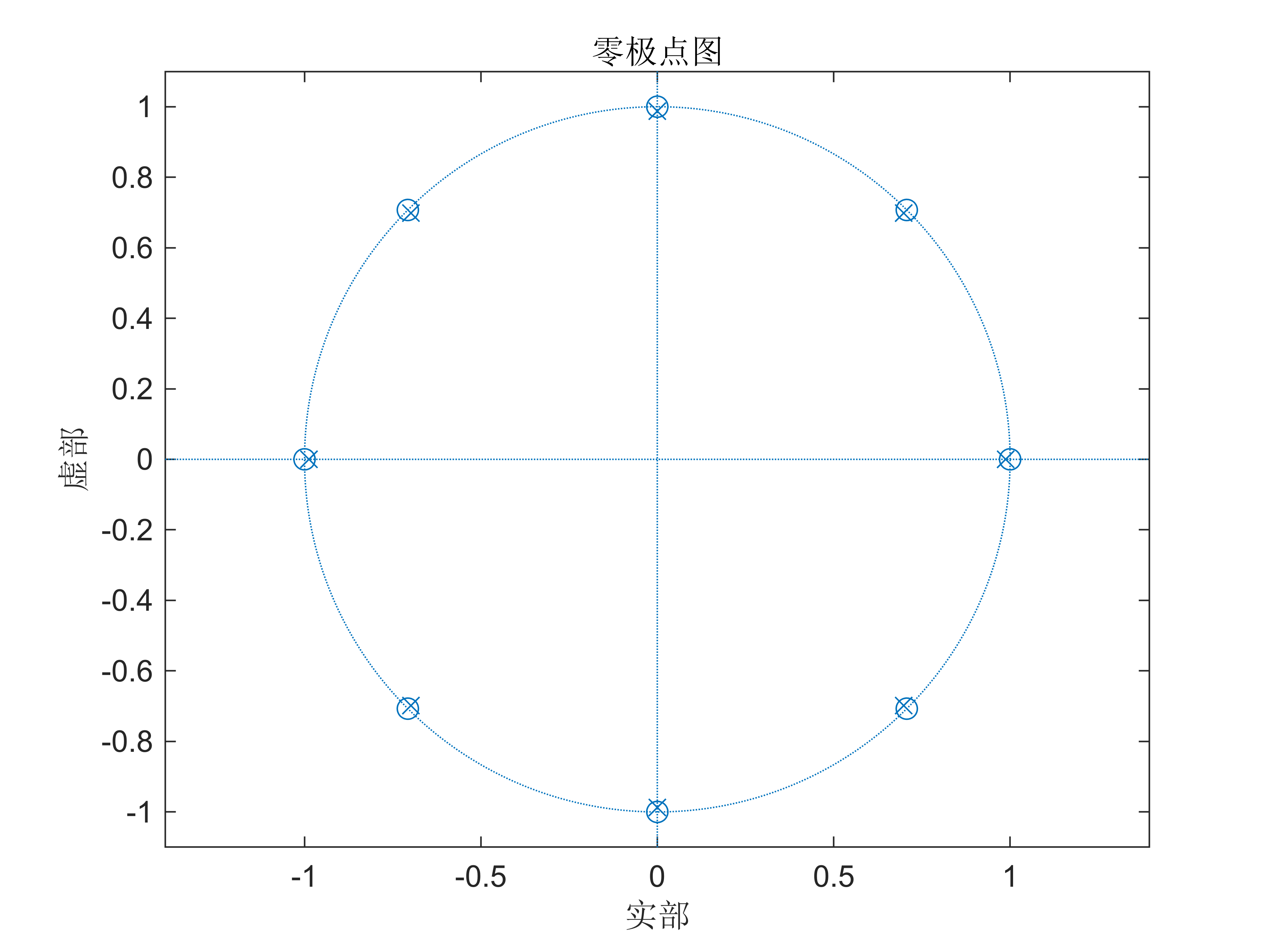
%% 问题2
% 计算频率响应,使用1024个点,覆盖整个频率范围[0, 2pi]
[H, w] = freqz(B, A, 1024, 'whole');% 计算频率响应的幅值和相位
Hm = abs(H); % 幅值
Hp = angle(H); % 相位subplot(211);
plot(w, Hm); % 绘制幅度曲线
grid on;
xlabel("omega(rad/s)");
ylabel('Magnitude');
title('离散系统幅频特性曲线'); subplot(212);
plot(w, Hp); % 绘制相位曲线
grid on;
xlabel("omega(rad/s)");
ylabel('Phase');
title('离散系统相频特性曲线');
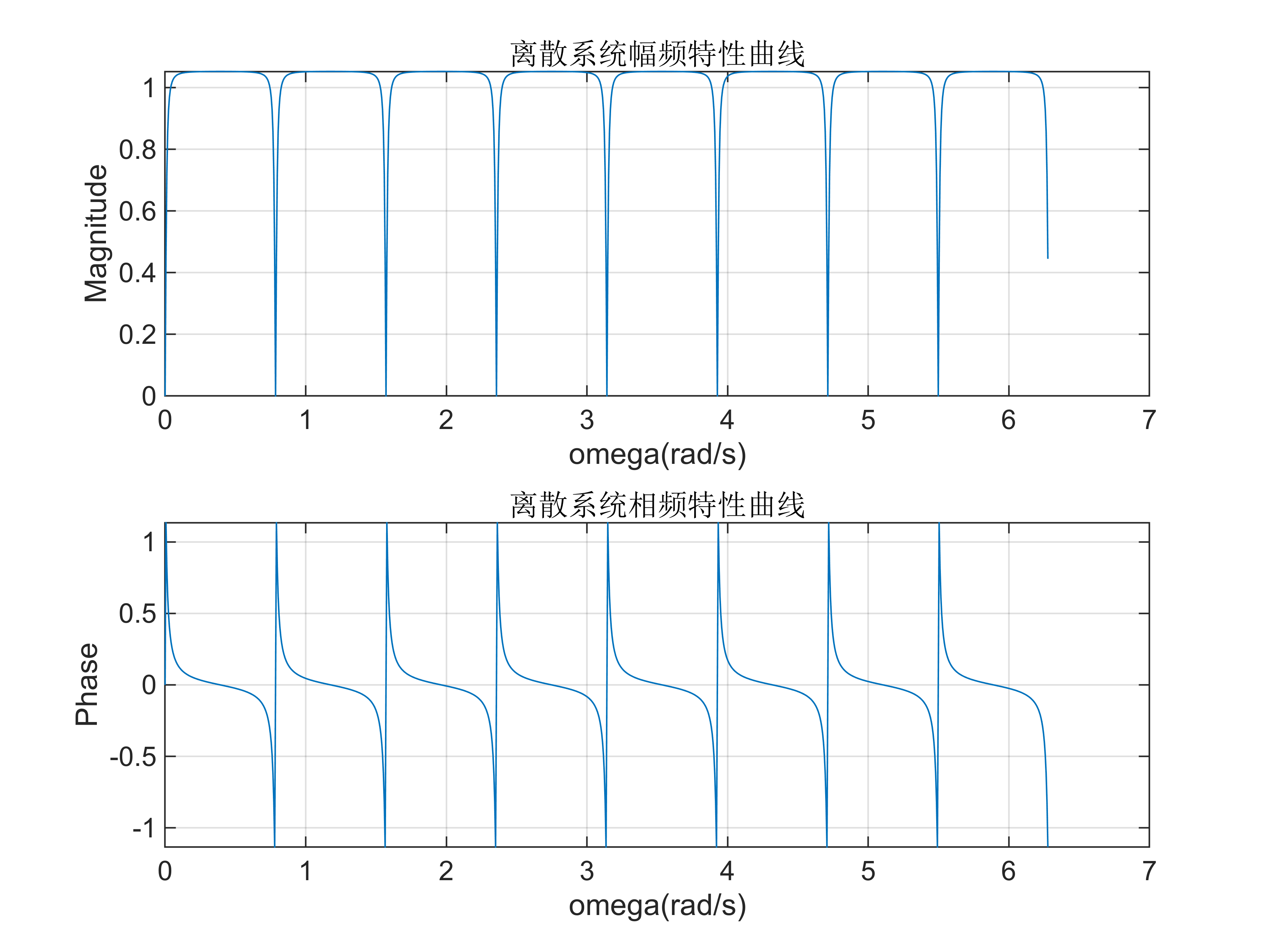
问题3
根据幅频和相频特性曲线,这个系统是梳状滤波器。这种滤波器可用于消除信号中的电网谐波干扰和其他频谱等间隔分布的干扰。
思考题
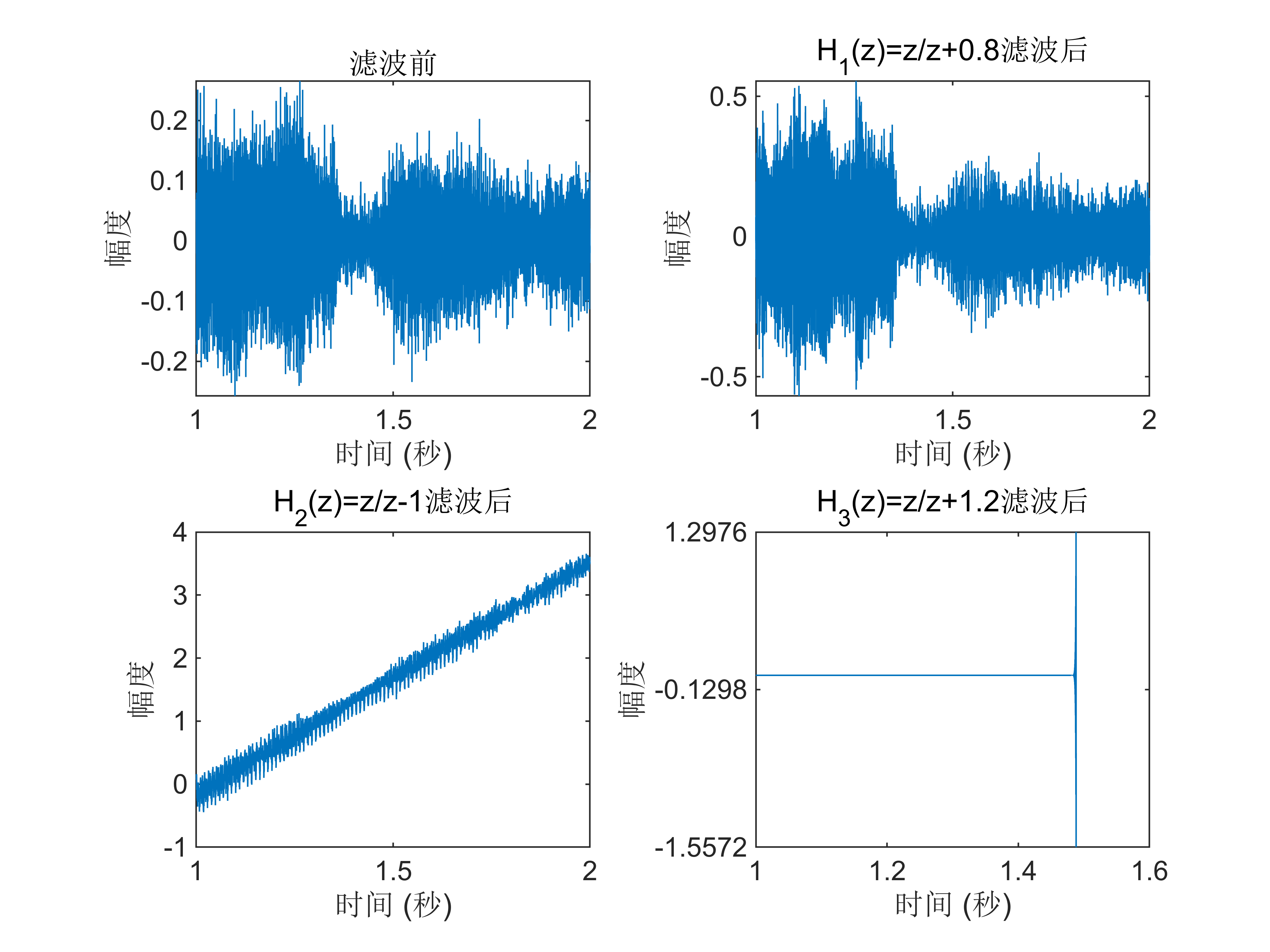
1. 编写 Matlab程序,分别采用系统对音频文件motherland.wav进行滤波(可采用实验二的 conv函数)。
(1)画出滤波前后该音频文件1~2s时间段 的连续时域波形图要求横坐标的单位为秒
(2)说明滤波后信号幅度变化的原因。
% 读取音频文件
[audio,fs] = audioread(...".\2024-2025(1)《信号处理实验》资料(请拷贝到u盘中,每次试验带到实验室)\实验中用到的一些函数和音频图像文件\motherland.wav"...
);
% 设置时长
start_time = 1;
end_time = 2;% 计算设置时间内的样本数
samplesPerSec = fs;
startSample = start_time * samplesPerSec + 1; % MATLAB索引从1开始
endSample = end_time * samplesPerSec;% 截取1~2秒的音频数据
audioSegment = audio(startSample:endSample, :);% 定义滤波器系数
b1 = [1 0];
a1 = [1 0.8];
b2 = [1 0];
a2 = [1 -1];
b3 = [1 0];
a3 = [1 1.2];% 应用滤波器
filteredAudio1 = filter(b1, a1, audioSegment);
filteredAudio2 = filter(b2, a2, audioSegment);
filteredAudio3 = filter(b3, a3, audioSegment);% 绘制滤波前后的时域波形
t = (0:length(audioSegment)-1) / fs; % 时间轴,单位为秒
figure;
subplot(2,2,1);
plot(t+start_time, audioSegment);
title('滤波前');
xlabel('时间 (秒)');
ylabel('幅度');subplot(2,2,2);
plot(t+start_time, filteredAudio1);
title('H_1(z)=z/z+0.8滤波后');
xlabel('时间 (秒)');
ylabel('幅度');
subplot(2,2,3);
plot(t+start_time, filteredAudio2);
title('H_2(z)=z/z-1滤波后');
xlabel('时间 (秒)');
ylabel('幅度');
subplot(2,2,4);
plot(t+start_time, filteredAudio3);
title('H_3(z)=z/z+1.2滤波后');
xlabel('时间 (秒)');
ylabel('幅度');
% 播放滤波后的音频
% sound(f3, fs);
% 播放滤波前的音频
% sound(audioSegment, fs);
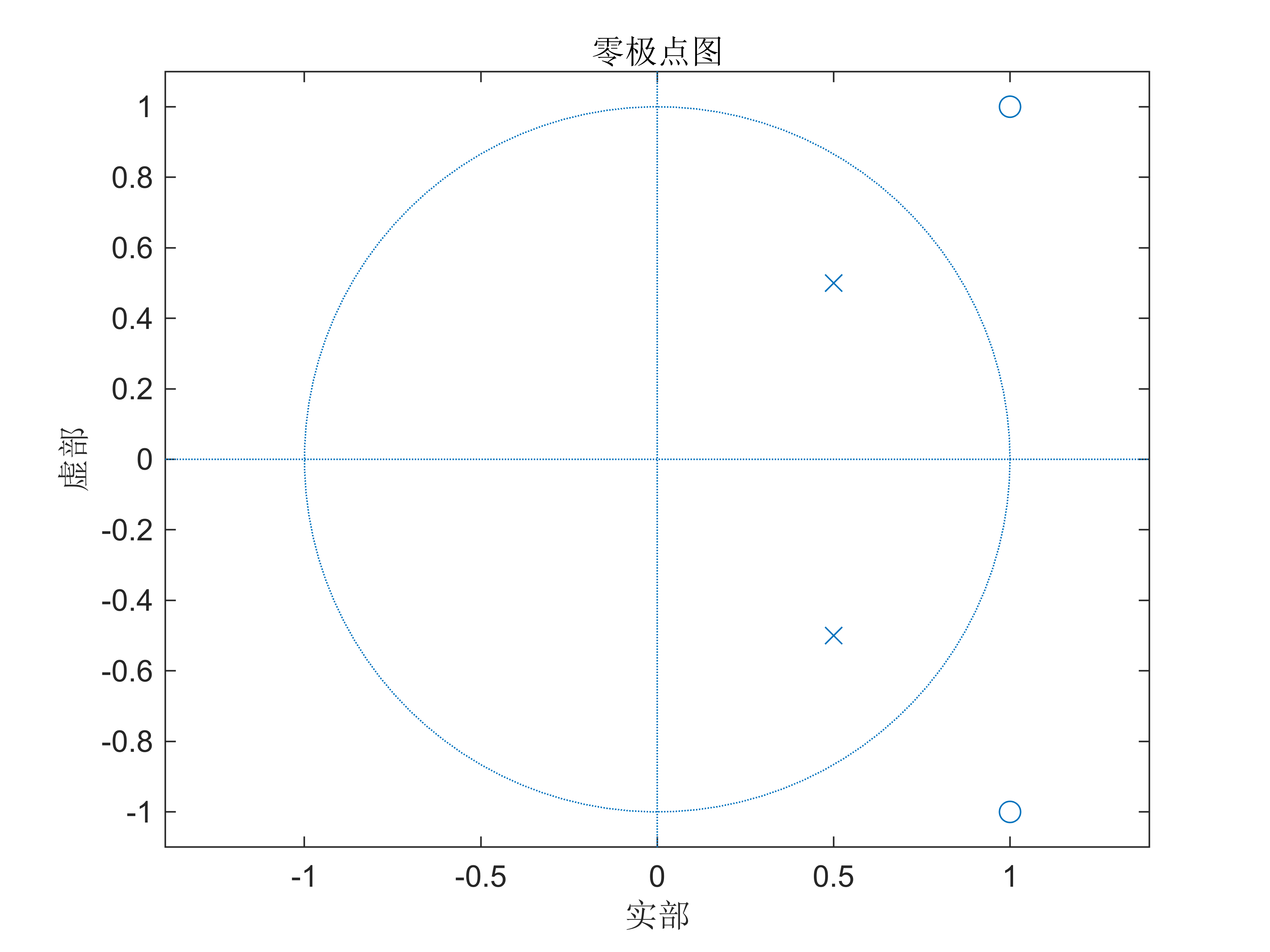
2. 已知系统函数 H ( z ) = z 2 − 2 z + 2 2 z 2 − 2 z + 1 H\left(z\right)=\frac{z^2 -2z+2}{2z^2 -2z+1} H(z)=2z2−2z+1z2−2z+2 编写 Matlab程序实现:
(1)画出该系统的零极点分布图,判断系统的稳定性
(2) 画出系统 在 0~2 π \pi π 范围内的幅频特性曲线和相频特性曲线;
(3) 查找资料说明该系统是什么类型的滤波器,在实际应用中有什么功能?
clear;close all;
B=[1 -2 2];
A=[2 -2 1];
%% 问题1
zplane(B,A)
%% 问题2
[H, w] = freqz(B, A, 1024, 'whole');% 计算频率响应的幅值和相位
Hm = abs(H); % 幅值
Hp = angle(H); % 相位% 创建第一个子图,绘制幅频特性曲线
subplot(211); % 将图形窗口分割为2行1列,并在第1个位置绘图
plot(w, Hm); % 绘制幅值曲线
grid on; % 显示网格
xlabel("\omega(rad/s)"); % x轴标签
ylabel('Magnitude'); % y轴标签
title('离散系统幅频特性曲线'); % 图形标题% 创建第二个子图,绘制相频特性曲线
subplot(212); % 在第2个位置绘图
plot(w, Hp); % 绘制相位曲线
grid on; % 显示网格
xlabel("\omega(rad/s)"); % x轴标签
ylabel('Phase'); % y轴标签
title('离散系统相频特性曲线'); % 图形标题
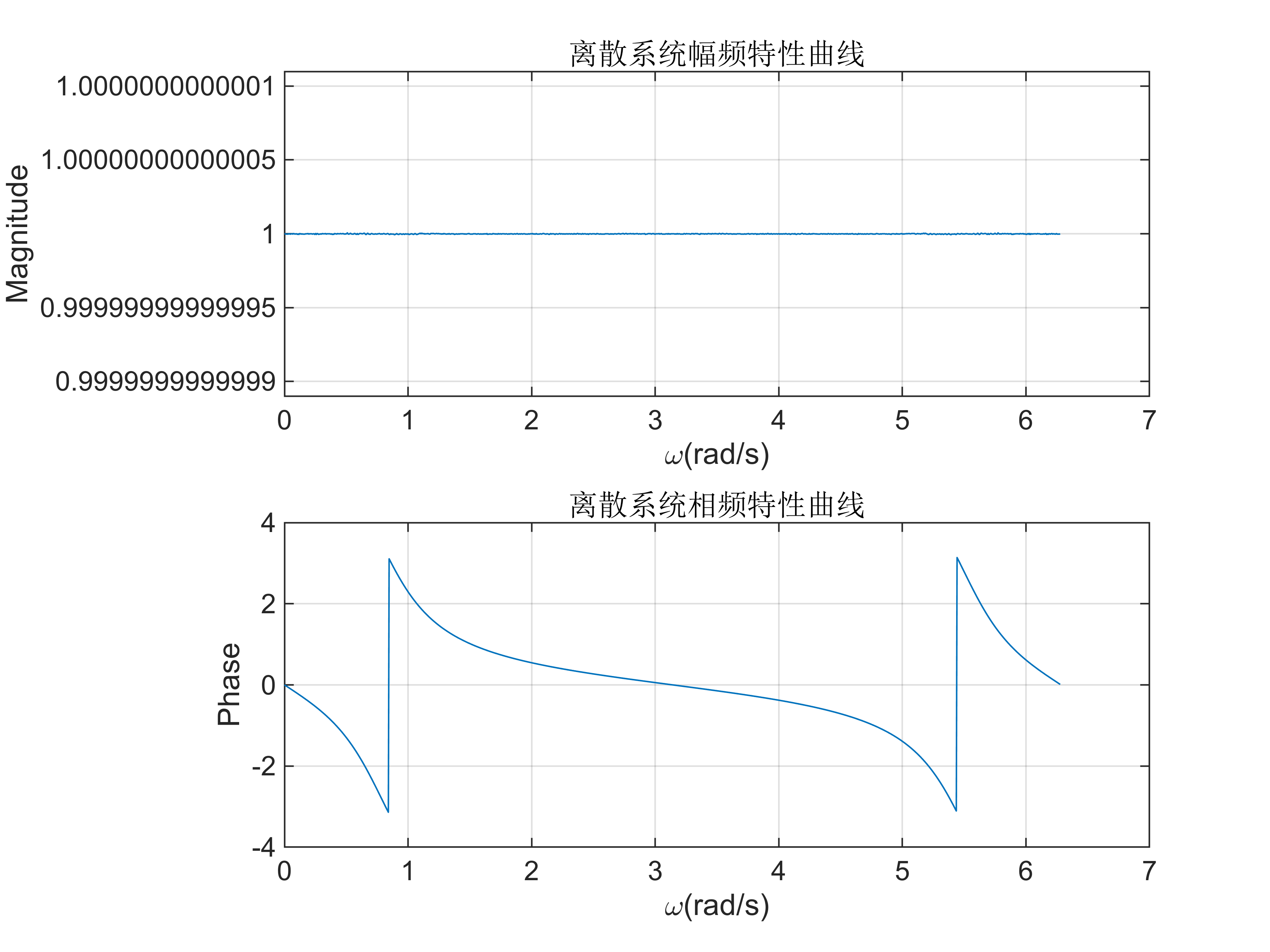
由此可知,该系统的所有极点均在 z 域单位圆内,与所画的零极图一致。由图可知,该系
统在 ω ∈ [0, 2π) 幅度值均为1,所以该系统是一个全通滤波器。








![[护网杯 2018]easy_tornado](https://i-blog.csdnimg.cn/direct/266982542f494ab3be1d2f53e6acfdb5.png)