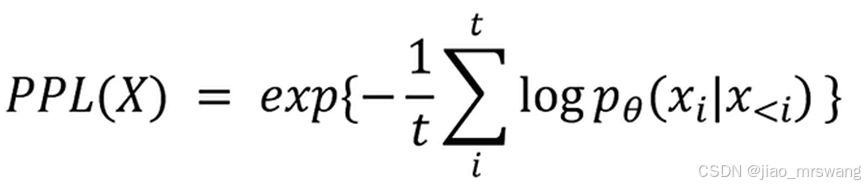剑指offer（专项突破）---字符串

总目录：剑指offer（专项突破）---目录-CSDN博客

1.字符串的基本知识

C语言中：

函数名	功能描述
`strcpy(s1, s2)`	将字符串`s2`复制到字符串`s1`中，包括结束符`'\0'`，要求`s1`有足够空间容纳`s2`的内容。
`strncpy(s1, s2, n)`	把`s2`中最多`n`个字符复制到`s1`中。若`s2`的长度小于`n`，则`s1`中剩余部分用`'\0'`填充；若`s2`长度大于等于`n`，则`s1`不会以`'\0'`结尾（需手动添加）。
`strcat(s1, s2)`	将字符串`s2`连接到字符串`s1`的末尾，`s1`要有足够空间容纳连接后的内容，会自动添加结束符`'\0'`。
`strncat(s1, s2, n)`	把`s2`中最多`n`个字符连接到`s1`的末尾，然后添加`'\0'`，`s1`要预留足够空间。
`strcmp(s1, s2)`	比较`s1`和`s2`两个字符串的大小，按照字典序进行比较。若`s1`小于`s2`返回负整数；若`s1`等于`s2`返回 0；若`s1`大于`s2`返回正整数。
`strncmp(s1, s2, n)`	比较`s1`和`s2`中前`n`个字符的大小，按照字典序比较，返回值规则同`strcmp`。
`strlen(s)`	计算字符串`s`的长度，不包括结束符`'\0'`，返回字符串中字符的个数。
`strchr(s, c)`	在字符串`s`中查找字符`c`第一次出现的位置，若找到返回指向该字符的指针，若没找到返回`nullptr`。
`strrchr(s, c)`	在字符串`s`中查找字符`c`最后一次出现的位置，若找到返回指向该字符的指针，若没找到返回`nullptr`。
`strstr(s1, s2)`	在字符串`s1`中查找字符串`s2`第一次出现的位置，若找到返回指向`s2`在`s1`中起始位置的指针，若没找到返回`nullptr`。

C++中：

函数名	功能描述
`size()`	返回字符串中字符的个数。
`length()`	获取字符串的长度，即字符个数。
`empty()`	判断字符串是否为空，为空返回`true`，否则返回`false`。
`clear()`	清空字符串内容，使其长度变为 0。
`push_back(c)`	在字符串末尾添加一个字符`c`。
`pop_back()`	删除字符串末尾的一个字符。
`compare(s2)`	比较当前字符串和`s2`的大小，按照字典序比较，返回值规则类似`strcmp`函数（小于返回负整数，等于返回 0，大于返回正整数）。
`substr(pos, n)`	从索引`pos`位置开始提取连续的`n`个字符，若`n`省略，则提取从`pos`开始到末尾的所有字符，返回提取出来的子字符串。
`find(s2, pos)`	从索引`pos`位置开始查找字符串`s2`第一次出现的位置，若找到返回位置索引，若没找到返回`std::string::npos`（一个特殊的表示未找到的值），若`pos`省略，则从开头查找。
`rfind(s2, pos)`	从索引`pos`位置开始查找字符串`s2`最后一次出现的位置，返回值规则同`find`函数，若`pos`省略，则从末尾往前查找。
`replace(pos, n, s2)`	将从索引`pos`开始的`n`个字符替换成字符串`s2`，若`n`省略，则替换从`pos`开始到末尾的所有字符。

2.双指针

第2章用两个指针来定位一个子数组，其中一个指针指向数组的第1个数字，另一个指针指向数组的最后一个数字，那么两个指针之间所包含的就是一个子数组。

如果将字符串看成一个由字符组成的数组，那么也可以用两个指针来定位一个子字符串，其中一个指针指向字符串的第1个字符，另一个指针指向字符串的最后一个字符，两个指针之间所包含的就是一个子字符串。

LCR 014. 字符串的排列 - 力扣（LeetCode）

题解：滑动窗口

数组模拟哈希表 cnt1 统计字符串 s1 中每个字符出现的次数，然后遍历字符串 s2，维护一个窗口大小为 m 的滑动窗口。

数组模拟哈希表 cnt2 统计窗口内每个字符出现的次数，当 cnt1=cnt2 时，说明窗口内的字符及其个数与字符串 s1 相同，返回 true 即可。

否则，遍历结束后，返回 false。

时间复杂度 (m+n×∣Σ∣)，空间复杂度 O(∣Σ∣)。其中 m 和 n 分别为字符串 s1 和 s2 的长度；而 ∣Σ∣ 为字符集的大小，本题中∣Σ∣=26。

class Solution 
{
public:bool checkInclusion(string s1, string s2) {int m = s1.size(), n = s2.size();if (m > n)return false;vector<int> cnt1(26), cnt2(26);for (int i = 0; i < m; ++i) {++cnt1[s1[i] - 'a'];++cnt2[s2[i] - 'a'];}if (cnt1 == cnt2)return true;for (int i = m; i < n; ++i) {++cnt2[s2[i] - 'a'];--cnt2[s2[i - m] - 'a'];if (cnt1 == cnt2)return true;}return false;}
};

优化：

每次加入和移除一个字符时，都需要比较两个哈希表，时间复杂度较高。我们可以维护一个变量 k，表示两个大小为 m 的字符串中，有多少种字符出现的个数不同。当 k=0 时，说明两个字符串中的字符个数相同。

时间复杂度 O(m+n+∣Σ∣)，空间复杂度 O(∣Σ∣)。其中 m 和 n 分别为字符串 s1 和 s2 的长度；而 ∣Σ∣ 为字符集的大小，本题中 ∣Σ∣=26。

class Solution 
{
public:bool checkInclusion(string s1, string s2) {int m = s1.size(), n = s2.size();if (m > n)return false;vector<int> cnt(26);for (int i = 0; i < m; ++i) {--cnt[s1[i] - 'a'];++cnt[s2[i] - 'a'];}int k = 0;for (int x : cnt)if (x != 0)++ k;if (k == 0)return true;for (int i = m; i < n; ++i) {int a = s2[i - m] - 'a';int b = s2[i] - 'a';if (cnt[a] == 0)++ k;-- cnt[a];if (cnt[a] == 0)-- k;if (cnt[b] == 0)++ k;++ cnt[b];if (cnt[b] == 0)-- k;if (k == 0)return true;}return false;}
};

LCR 015. 找到字符串中所有字母异位词 - 力扣（LeetCode）

题解：滑动窗口

同LCR 014，优化方式也一样，添加一个差异计数器

class Solution 
{
public:vector<int> findAnagrams(string s, string p) {int m = s.size();int n = p.size();vector<int> ans;if (m < n)return ans;vector<int> cnt1(26), cnt2(26);for (int i = 0; i < n; ++i) {++cnt1[s[i] - 'a'];++cnt2[p[i] - 'a'];}if (cnt1 == cnt2)ans.push_back(0);for (int i = n; i < m; ++i) {++cnt1[s[i] - 'a'];--cnt1[s[i - n] - 'a'];if (cnt1 == cnt2)ans.push_back(i - n + 1);}return ans;}
};

LCR 016. 无重复字符的最长子串 - 力扣（LeetCode）

题解：双指针 + 哈希表

遍历字符串 s，对于当前遍历到的字符 s[r]，如果 s[r] 在 [l,r) 范围内有与 s[r] 相同的字符，我们就不断地向右移动指针 l，直到 ss[s[r]] 为 false，此时 [l,r) 中没有任何与 s[r] 相同的字符，我们就找到了以字符 s[r] 为结尾的最长子串。更新最长子串的长度，最终返回答案。

时间复杂度 O(n)，空间复杂度 O(∣Σ∣)，其中 n 为字符串 s 的长度，而 Σ 表示字符集，本题中字符集为所有 ASCII 码在 [0,128) 内的字符，即∣Σ∣=128。

class Solution 
{
public:int lengthOfLongestSubstring(string s) {bool ss[128] = {false};int ans = 0;for (int l = 0, r = 0; r < s.size(); ++ r) {while (ss[s[r]])ss[s[l++]] = false;ss[s[r]] = true;ans = max(ans, r - l + 1);}return ans;}
};

LCR 017. 最小覆盖子串 - 力扣（LeetCode）

题解：滑动窗口

外层while循环 - 窗口扩张：
while(r < s.size())：这个循环的条件是只要r指针还没遍历完整个字符串s，就持续向右移动r指针来扩展窗口，模拟窗口不断向右滑动去尝试包含t中所有字符的过程。
char i = s[r++];：每次获取r指针指向的字符，并将r指针后移一位来扩大窗口范围。
if(++curHash[i] <= baseHash[i])：将该字符在curHash数组中的出现次数加 1，然后判断加 1 后的次数是否小于等于其在baseHash数组中记录的t里该字符出现的次数。若成立，则将计数器count加 1。
内层while循环 - 窗口收缩：
while(count == t.size())：当count的值等于字符串t的长度时，意味着当前窗口已经包含了t中的所有字符，此时就进入内层循环来尝试收缩窗口，看能否找到更小的符合条件的窗口。
if(r-l < minLen)：判断当前窗口的长度（r - l）是否小于已记录的最小窗口长度minLen，如果是，则更新k为当前窗口的起始位置l，更新minLen为当前窗口的长度，即找到了一个更短的包含t所有字符的窗口。
char o = s[l++];：从窗口的左边开始收缩，获取要移出窗口的字符，并将l指针后移一位。
if(curHash[o]-- <= baseHash[o])：将该字符在curHash数组中的出现次数减 1，然后判断减 1 后的次数是否小于等于其在baseHash数组中记录的t里该字符出现的次数。若成立，则将计数器count减 1。

两个指针 l 和 r 都是从最左端向最右端移动，且 l 的位置一定在r 的左边或重合。注意本题虽然在 while 循环里出现了一个 while 循环，但是因为内循环负责移动 l 指针，且 l 只会从左到右移动一次，因此总时间复杂度仍然是 O(n)。

class Solution
{
public:string minWindow(string s, string t){//先统计字符情况int baseHash[128] = { 0 }, curHash[128] = { 0 };for(auto& ch : t){++baseHash[ch];}int k = 0, minLen = s.size() + 1;//k:记录窗口起始位置 minLen:记录最小窗口长度int l = 0, r = 0, count = 0;//外层循环：窗口扩张while(r < s.size()){char i = s[r++];if(++curHash[i] <= baseHash[i]){++count;}//内层循环：窗口收缩while(count == t.size()){if(r-l < minLen){k = l;minLen = r-l;}char o = s[l++];if(curHash[o]-- <= baseHash[o]){--count;}}}return minLen > s.size() ? "" : s.substr(k, minLen);}
};

3.回文字符串

LCR 018. 验证回文串 - 力扣（LeetCode）

题解：双指针

时间复杂度 O(n)。空间复杂度 O(1)。

class Solution 
{
public:bool isPalindrome(string s) {int l = 0, r = s.size() - 1;while (l < r) {while (l < r && !isalnum(s[l]))++ l;while (l < r && !isalnum(s[r]))-- r;if (tolower(s[l]) != tolower(s[r]))return false;++ l;-- r;}return true;}
};

LCR 019. 验证回文串 II - 力扣（LeetCode）

题解：双指针 + 递归

时间复杂度 O(n)。空间复杂度 O(1)。

class Solution 
{
public:bool validPalindrome(string s) {auto check = [&](int i, int j) {for (; i < j; ++i, --j)if (s[i] != s[j])return false;return true;};for (int i = 0, j = s.size() - 1; i < j; ++i, --j) if (s[i] != s[j])return check(i + 1, j) || check(i, j - 1);return true;}
};

LCR 020. 回文子串 - 力扣（LeetCode）

题解1：从中心向两侧扩展回文串

外层循环：遍历字符串每一位

内层循环：分别计算当前字符为中心点及当前字符与下一位字符为中心点

时间复杂度 O(n^2)。

class Solution 
{
public:int countSubstrings(string s) {int ans = 0;auto f = [&](int i, int j) -> int {int cnt = 0;for (; i >= 0 && j < s.size() && s[i] == s[j]; -- i, ++ j)++cnt;return cnt;};for (int i = 0; i < s.size(); ++ i)ans += f(i, i) + f(i, i + 1);return ans;}
};

题解2：Manacher 算法

在 Manacher 算法的计算过程中，用 p[i]−1 表示以第 i 位为中心的最大回文长度，以第 i 位为中心的回文串数量为 $\left \lceil \frac{p[i] - 1}{2} \right \rceil$ 。

时间复杂度 O(n)，空间复杂度 O(n)。

class Solution 
{
public:int countSubstrings(string s) {int n = s.size();string t = "!#";for (const char &c: s) {t += c;t += '#';}n = t.size();t += '$';auto f = vector <int> (n);int mid = 0, rMax = 0, ans = 0;for (int i = 1; i < n; ++i) {// 初始化 f[i]f[i] = (i <= rMax) ? min(rMax - i + 1, f[2 * mid - i]) : 1;// 中心拓展while (t[i + f[i]] == t[i - f[i]]) ++f[i];if (i + f[i] - 1 > rMax) {mid = i;rMax = i + f[i] - 1;}// 当前贡献为 (f[i] - 1) / 2 上取整ans += (f[i] / 2);}return ans;}
};