MATLAB是一种强大的数学软件,广泛应用于工程计算、控制设计、信号处理等领域。在数学建模中,MATLAB的绘图功能可以帮助我们直观地展示数据和模型结果。
1. 二维数据曲线图
1.1 绘制二维曲线的基本函数
plot函数用于绘制二维平面上的线性坐标曲线图,要提供一组x坐标和对应的y坐标,可以绘制分别以x和y为横、纵坐标的二维曲线。 例如绘制一函数曲线:
t=0:0.1:2*pi;
x=2 * t;
y=t.*sin(t).*sin(t);
plot(x, y);
plot函数可以包含若干组向量对,每一组可以绘制出一条曲线,含多个输入参数的plot函数调用格式为plot(x1,y1,x2,y2,…,xn,yn) 。
x=linspace(0,2*pi,100);
plot(x,sin(x),x,2*sin(x),x,3*sin(x))
Matlab提供了一些绘图选项,用于确定所绘曲线的线型、颜色和数据点标记符号。可以用不同的线型和颜色在同一坐标内绘制曲线及其包络线:
x=(0:pi/100:2*pi)';
y1=2*exp(-0.5*x)*[1,-1];
y2=2*exp(-0.5*x).*sin(2*pi*x);
x1=(0:12)/2;
y3=2*exp(-0.5*x1).*sin(2*pi*x1);
plot(x,y1,'k:',x,y2,'b--',x1,y3,'rp');
在该plot函数中包含了3组绘图参数,第一组用黑色虚线画出两条包络线,第二组用蓝色双划线画出曲线y,第三组用红色五角星离散标出数据点。
设置正弦曲线的线宽为 3,设置上三角形进行数据点的标记,并设置标记 点边缘为黑色,设置标记点填充颜色为红色,设置标记点的尺寸为 10,则 MATLAB 代码 如下:
% 横坐标轴
x = linspace(0, 2*pi, 50);
% 生成数据点,纵坐标轴
y = 2 * sin(pi * x);
% 绘图
figure
% 设置线的宽带为3
plot(x, y, 'k--^', 'LineWidth', 3, ... 'MarkerEdgeColor', 'k', ... %设置标记点的边缘颜色为黑色 'MarkerFaceColor', 'r', ... %设置标记点的填充颜色为红色 'MarkerSize', 10) %设置标记点的尺寸为10 
利用五角星标记例两曲线的交叉点:
% 横坐标轴
x = linspace(0, 2*pi, 1000);
% 生成数据点,纵坐标轴
y1 = 0.2 * exp(-0.5 * x).* cos(4 * pi * x);
y2 = 2 * exp(-0.5 * x) .* cos(pi * x);
% 查找y1与y2相等点(近似相等)的下标
k = find( abs(y1-y2) < 1e-2 );
%取y1与y2相等点的x坐标
x1 = x(k);
% 求y1与y2值相等点的y坐标
y3 = 0.2 * exp(-0.5 * x1) .* cos(4 * pi * x1);
% 绘图
figure
plot(x, y1, 'r-.', x, y2, 'k:', x1, y3, 'bp','LineWidth',2); 
在Matlab中,如果需要绘制出具有不同纵坐标标度的两个图形,可以使用plotyy函数,它能把具有不同量纲,不同数量级的两个函数绘制在同一个坐标中,有利于图形数据的对比分析。使用格式为plotyy(x1,y1,x2,y2) ,其中x1,y1对应一条曲线,x2,y2对应另一条曲线。横坐标的标度相同,纵坐标有两个,左边的对应x1,y1数据对,右边的对应x2,y2。
x=0:pi/100:2*pi;
% 生成曲线
y1=0.2*exp(-0.5*x).*cos(4*pi*x);
y2=2*exp(-0.5*x).*cos(pi*x);
% 绘图
figure
plotyy(x,y1,x,y2);
plot(x, y1, 'k-', x, y2, 'k-', 'LineWidth', 3) 
1.2 绘制图形的辅助操作
title、xlabel和ylabel函数分别用于说明图形和坐标轴的名称,text函数是在坐标点(x,y)处添加图形说明,legend函数用于绘制曲线所用线型、颜色或数据点标记图例,图例放置在空白处,用户还可以通过鼠标移动图例,将其放到所希望的位置。
除legend函数外,其他函数同样适用于三维图形,在三维中z坐标轴说明用zlabel函数。绘制正弦和余弦曲线,设置图形的标题、x 轴和 y 轴的标注,设置曲线标准。
% 横轴
x=0:pi/50:2*pi;
% 曲线数据
y1=sin(x);
y2=cos(x);
% 绘图
figure
plot(x, y1, 'k-', x, y2, 'k-.')
% 文本标注
text(pi, 0.05, '\leftarrow sin(\alpha)')
text(pi/4-0.05, 0.05, 'cos(\alpha)\rightarrow')
% 标题标注
title('sin(\alpha) and cos(\alpha)')
% 坐标轴标注
xlabel('\alpha')
ylabel('sin(\alpha) and cos(\alpha)')
使用axis函数进行坐标控制,如果给出前四个参数,则按照给出的x、y轴的最小值和最大值选择坐标系范围,绘制出合适的二维曲线。如果给出全部参数,则绘制出三维图形。
% x轴
x = 0:1/3000:1;
% 生成误差曲线
y = cos(tan(pi*x));
% 绘图
figure
% 分裂窗口为2*1个子窗口
subplot(2,1,1)
plot(x,y)
title('\itcos(tan(\pix))')
% 坐标轴调整
subplot(2,1,2)
plot(x,y)
axis([0.4 0.6 -1 1]);
title('复杂函数的局部透视')
1.3 绘制二维图形的其他函数
在实际应用中,经常用到对数坐标,Matlab提供了绘制对数和半对数坐标曲线的函数,这些函数中选项的定义和plot函数完全一样,所不同的是坐标轴的选取。
% x轴
x=0:0.5:5;
% y轴
y = exp(x);
% 绘图
figure
% 笛卡尔坐标系
subplot(4, 1, 1)
plot(x, y, 'r-.')
title('笛卡尔坐标系')
% 半对数坐标系
subplot(4, 1, 2)
semilogx(x, y, 'g:')
title('x轴为对数坐标系')
subplot(4, 1, 3)
semilogy(x, y, 'b-')
title('y轴为对数坐标系')
% 对数坐标系
subplot(4, 1, 4)
loglog(x, y, 'k:','LineWidth',4)
title('对数坐标系')
饼图、条形图和排列图(箱线图)也是很常用的数据可视化工具,它们各自适用于不同的数据展示场景。
2. 三维图形绘制
2.1 绘制三维曲线
plot3()函数将二维绘图函数plot的有关功能扩展到三维空间,可以用来绘制三维曲线。其调用格式为 plot3(x1,y1,z1,选项1,x2,y2,z2,选项2,…),其中每一组x,y,z组成一组曲线的坐标参数,选项的定义和plot的选项一样。当x,y,z是同维向量时,则x,y,z对应元素构成一条三维曲线。当x,y,z是同维矩阵时,则以x,y,z对应列元素绘制三维曲线,曲线条数等于矩阵的列数。
t=0:pi/50:2*pi;
x=8*cos(t);
y=4*sqrt(2)*sin(t);
z=-4*sqrt(2)*sin(t);
plot3(x,y,z,'p');
title('Line in 3-D Space');
text(0,0,0,'origin');
xlabel('X');ylabel('Y');zlabel('Z');grid;
进行三维图形绘制时,常常需要首先创建三维网格,也就是先创建平面图的坐标系。在 MATLAB 中,常用meshgrid()函数生成网格数据。
由于网格线是不透明的,绘制的三维网格图有时只能显示前面的图形部分,而后面的部分可能被网格线遮住没有显示,MATLAB中提供了命令 hidden 用于观察图形后面隐藏的网格。
% 数据准备
t=0:pi/10:pi;
x=sin(t);
y=cos(t);
[X,Y]=meshgrid(x,y);
z =X + Y;
% 绘图
figure
mesh (z,'FaceColor','W','EdgeColor','K')
grid
title('三维网格图'); 
2.2 三维表面图的绘制
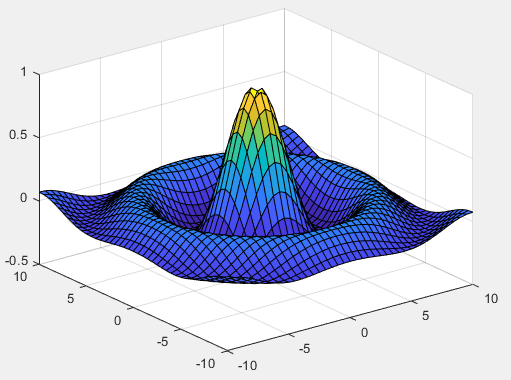
三维表面图也可以用来表示三维空间内数据的变化规律,与之前讲述的三维网络图的不同之处在于对网格的区域填充了不同的色彩,在 MATLAB 中绘制三维表面图的函数为surf()函数。
% 数据准备
xi=-10:0.5:10;
yi=-10:0.5:10;
[x,y]=meshgrid(xi,yi);
z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2);
% 绘图
surf(x,y,z)