
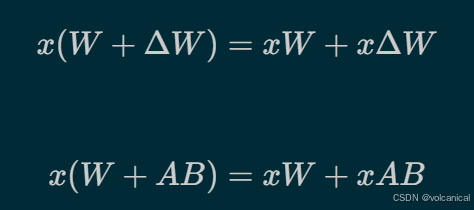
传统的微调,即微调全量参数,就是上面的公式,但是我们可以通过两个矩阵,来模拟这个全量的矩阵,如果原来的W是(N * N)维度,我们可以通过两个(N * R) 和 (R * N)的矩阵矩阵乘,来模拟微调的结果。
方法很简单,直接上代码
1. LoRA层:
import mathclass LoRALayer(torch.nn.Module):def __init__(self, in_dim, out_dim, rank, alpha):super().__init__()self.A = torch.nn.Parameter(torch.empty(in_dim, rank))torch.nn.init.kaiming_uniform_(self.A, a=math.sqrt(5)) # similar to standard weight initializationself.B = torch.nn.Parameter(torch.zeros(rank, out_dim))self.alpha = alphadef forward(self, x):x = self.alpha * (x @ self.A @ self.B)return x
LoRALayer就是LoRA的旁侧连接,包括了两个矩阵A和B,A初始化,但是B是全0矩阵,这保证一开始LoRA对模型没有影响,即输出和原来完全相同。
我们注意到了两个参数,一个是rank,一个是alpha。rank控制了LoRA旁侧连接的秩,这就是LoRA微调参数量较小的原因所在,因为他是由两个小的矩阵构成的。alpha控制LoRA对原来Linear的影响。
2. LoRA替代层
知道了LoRA的原理,现在只需要在模型中加入LoRA即可。但是LoRA要如何加入呢,在模型中加入的话,需要修改前向传播的逻辑才能人为的修改,不难想到另外一种方法,我们直接替代原来的Linear层,用LinearWithLoRA替换,新的层既有原来的Linear,也有LoRA。
class LinearWithLoRA(torch.nn.Module):def __init__(self, linear, rank, alpha):super().__init__()self.linear = linearself.lora = LoRALayer(linear.in_features, linear.out_features, rank, alpha)def forward(self, x):return self.linear(x) + self.lora(x)
3. 冻结原始参数
total_params = sum(p.numel() for p in model.parameters() if p.requires_grad)
print(f"Total trainable parameters before: {total_params:,}")for param in model.parameters():param.requires_grad = Falsetotal_params = sum(p.numel() for p in model.parameters() if p.requires_grad)
print(f"Total trainable parameters after: {total_params:,}")
4. 修改网络
最后,我们只需要遍历网络,得到所有Linear层,并将他们设置为LinearWithLoRA即可。
def replace_linear_with_lora(model, rank, alpha):for name, module in model.named_children():if isinstance(module, torch.nn.Linear):# Replace the Linear layer with LinearWithLoRAsetattr(model, name, LinearWithLoRA(module, rank, alpha))else:# Recursively apply the same function to child modulesreplace_linear_with_lora(module, rank, alpha)



















