每日一刷——二叉树的构建—

第一题：最大二叉树

题目描述：654. 最大二叉树 - 力扣（LeetCode）

我的想法：

我感觉这个题目最开始大家都能想到的暴力做法就是遍历找到数组中的最大值，然后再遍历一遍，把在它左边的依次找到最大值，但是emmm，感觉效率很低，时间上肯定过不了

然后其实我会觉得这个题目跟大根堆和小根堆有一点像，，，就是先建立一个树来，然后如果大就上去，如果小就下来，但是有一点，怎么保证顺序？？因为这样先建立一棵树来，再上移，好像不能保证？？我浅浅画个图

那这样，是让6之后的全部向上移动吗，移动到6的右边？

题目分析：

嗯，看了一圈，好像没有人用小根堆，大根堆写哈，有用单调栈写的，有用DFS写，然后其实我那个初始想法版本也行，因为我的题解给我的就是这样写的，但是有一点不一样的是：它分割了数组+递归，我就是憨憨的非要把每一步写出来哈，，其实每一个节点做的事情一样，就一定一定抽象出来然后递归

就是相当于先找到数组中的最大值，然后左右两边分别交给左右儿子再去做分割

其实这样我们可以总结一个思想就是：

其实每一个节点，都是首先把自己构造出来，然后想办法构造自己的左右子树，就相当于每一个人都有当孩子和当父亲的一天，你要在孩子时期规定此时要做的事，要在父亲时期规定要做的事，然后每一个人的框架都是如此，只不过最后做出来的成果可能不一样

我的错误题解：

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {// 只要不断地传递就可以了，天哪噜return build(nums, 0, nums.length - 1);}TreeNode build(int[] nums ,int lo,int hi){if(lo>hi)return null;int max=nums[lo];int index=lo;//找到数组中地最大值，然后构建这个节点，再分配左右儿子的数组for(int i=lo+1;i<=hi;i++){if(nums[i]>max){max=nums[i];index=i;}}//一般,数组，====>传递下标,而不是非得要找到这个数是多少//创建这个节点TreeNode root =new TreeNode(max);root.left=build(nums,lo,index-1);root.left=build(nums,index+1,hi);return root;}
}

其实这个错误原因很好分析，一看，我去，右边的好像都没进去，所以直接检查代码，发现root.right写错了，写成了root.left

题解：

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {// 只要不断地传递就可以了，天哪噜return build(nums, 0, nums.length - 1);}TreeNode build(int[] nums ,int lo,int hi){if(lo>hi)return null;int max=nums[lo];int index=lo;//找到数组中地最大值，然后构建这个节点，再分配左右儿子的数组for(int i=lo+1;i<=hi;i++){if(nums[i]>max){max=nums[i];index=i;}}//一般,数组，====>传递下标,而不是非得要找到这个数是多少//创建这个节点TreeNode root =new TreeNode(max);root.left=build(nums,lo,index-1);root.right=build(nums,index+1,hi);return root;}
}

这个题目想清楚了之后，代码写起来和思维都不是很难的

第二题：从前序与中序遍历序列构造二叉树

题目描述：105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）

我的想法：

soga，这个！用前序和中序构建树，这个题目老师原来讲过，挺经典的题的

而且无论是前序还是后序，都必须要知道中序序列，才有唯一的二叉树确定

应该思路是这样的：

先从preorder里边开始，最开始是3 然后在inorder里边找3，3就把inorder分成了两半，左边是左子树里边的，右边就是右子树里边的，然后一直一直这样下去，最后这棵树就建好了（这里的思路有点小问题，看到后面就知道了）

我的题解：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public TreeNode buildTree(int[] preorder, int[] inorder) {//1.建立头节点//拿到头节点在inorder中的位置，然后分割左右//左边就是新的inorder 右边也是新的inorder//2.建立左右子节点//3.什么时候结束？int index=0;return build(index,preorder,inorder,0,inorder.length-1);}public static TreeNode build(int index,int[] preorder, int[] inorder,int lf,int lr){if(lf<lr)return null;int findplace=0; TreeNode root =new TreeNode(preorder[index-1]);index++;for(int i=0;i<inorder.length;i++){if(inorder[i]==root.val){findplace=i;break;}}//突然感觉index传的不对啊？？？  这个index是互通的吗？？root.left=build(index,preorder,inorder,lf,findplace-1);root.right=build(index,preorder,inorder,findplace+1,lr);return root;}
}

为啥越界了？？？

题目分析：

for循环遍历确定index效率不高，可以考虑进一步优化：

因为题目说二叉树结点的值不重复，所以我们可以使用一个hashmap存储元素到索引的映射，这样就可以直接通过hashMap查到rootVal对应的index！！

我天！！！我知道了我的有一点的错误了！！

就是在preorder里边遍历，其实是不需要一个一个遍历，怎么说呢，因为你一直把index传给左右两颗子树，但是其实左右两颗子树里边需要的index并不相同，因为它们的元素就不相同，所以这样干，没有考虑周到，笑死我了，根据下面这张图应该能很明显的看到：preorder其实把它分成了这样两个部分

也就是说现在想指向某个值在数组里边对应的下标的时候，可以不需要遍历，直接用hashmap映射就可以了，它的值就是它的下标

题解：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public static HashMap<Integer,Integer> valToIndex =new HashMap<>();public TreeNode buildTree(int[] preorder, int[] inorder) {//1.建立头节点//拿到头节点在inorder中的位置，然后分割左右//左边就是新的inorder 右边也是新的inorder//2.建立左右子节点//3.什么时候结束？//HashMap优化for(int i=0;i<preorder.length;i++){valToIndex.put(inorder[i],i);}return build(0,preorder.length-1,preorder,inorder,0,inorder.length-1);}public static TreeNode build(int preFirst,int preLast,int[] preorder, int[] inorder,int lf,int lr){if(preFirst>preLast)return null;//分步完善  rootVal   index   leftSizeint rootVal =preorder[preFirst];int index=valToIndex.get(rootVal);int leftSize=index-lf;//构造父结点TreeNode root =new TreeNode(rootVal);/*有了hashmap这一步可以简化了for(int i=0;i<inorder.length;i++){if(inorder[i]==root.val){findplace=i;break;}} */root.left=build(preFirst+1 , preFirst+leftSize , preorder , inorder , lf , index-1);root.right=build(preFirst+leftSize+1 , preLast , preorder , inorder , index+1 , lr);return root;}
}

第三题：根据前序和后序遍历构造二叉树

题目描述：889. 根据前序和后序遍历构造二叉树 - 力扣（LeetCode）

我的想法：

我没有想法，惹惹惹，我在想这两个题有啥区别

我的题解：

题目分析：

前两道题：可以通过前序或者后序遍历找到根节点，然后根据中序遍历结果确定左右子树

但这一道题，可以确定根节点，但是无法确切的知道左右子树有哪些节点

比如：

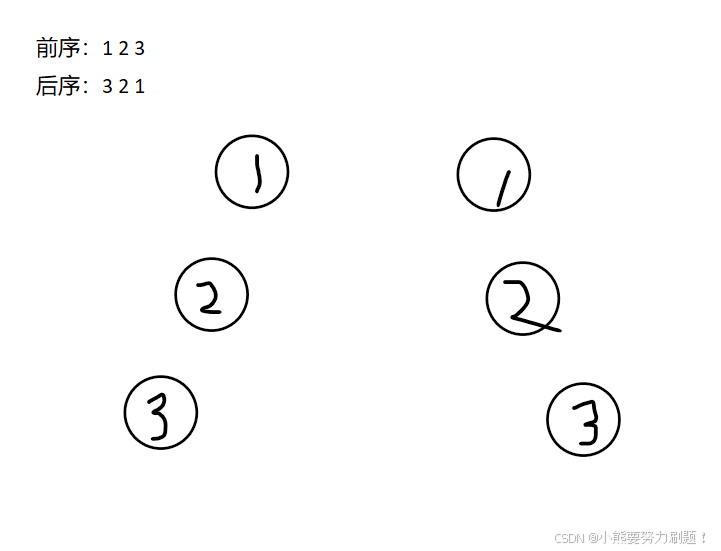
但是解法还是和前两道题差别不大，通过控制左右子树的索引来构建

1.首先把前序遍历结果的第一个元素或者后序遍历结果的最后一个元素作为根节点的值

2.然后把前序遍历结果的第二个元素作为左子树的根节点的值

3.在后序遍历结果中寻找左子树跟节点的值，从而确定了左子树的索引边界，进而确定右子树的索引边界，然后递归构造左右子树即可

题解：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {//依然是下标到数的hash映射HashMap<Integer,Integer> valToIndex =new HashMap<>();public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {for(int i=0;i<postorder.length;i++){valToIndex.put(postorder[i],i);}return build(preorder,0,preorder.length-1,postorder,0,postorder.length-1);}TreeNode build(int[] preorder,int preStart ,int preEnd,int[] postorder,int postStart,int postEnd){if(preStart > preEnd)return null;if(preStart==preEnd)return new TreeNode(preorder[preStart]);//root节点对应的值就是前序遍历数组的第一个元素int rootVal =preorder[preStart];//root.left 的值是前序遍历元素第二个元素//通过前序和后序遍历构造二叉树的关键在于通过左子树的根节点//确定preorder  和postorder 中左右子树的元素区间int leftRootVal =preorder[preStart+1];  //leftRootVal 在后序遍历数组中的索引int index =valToIndex.get(leftRootVal);//左子树的元素个数int leftSize =index-postStart +1;//先构造出当前根节点TreeNode root =new TreeNode(rootVal);//递归构造左右子树//根据左子树的根节点索引和元素个数推导左右子树的索引边界root.left =build(preorder,preStart+1,preStart+leftSize,postorder,postStart,index);root.right =build(preorder,preStart+leftSize+1,preEnd,postorder,index+1,preEnd-1); //是因为左闭右开吗？？         //好像因为要用到两个，preorder里边，一次性用两个，第一个为头节点，第二个为左孩子节点return root;}
}

我要背题目！！阿巴