数学归纳法

数学归纳法是以一种不同的方式来证明任意一个给定的情形都是正确的（第一个,第二个，第三个，一直下去概不例外）的数学定理。
但是数学归纳法并非不严谨的归纳推理法，它属于完全严谨的“演绎推理法”。事实上，所有数学证明都是演绎法。

实际以多米诺效应推导

1、证明第一张骨牌会倒。
2、证明只要任意一张骨牌倒了，那么与其相邻的下一张骨牌也会倒。
及可证明： 所有的骨牌都会倒下。

求证等差数列结论是否正确：

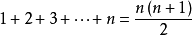——等差数列求和公式
第一步，验证该公式在 n = 1 时成立。即有左边=1，右边= =1，所以这个公式在n = 1时成立。
第二步，需要证明假设n = m 时公式成立，那么可以推导出n = m+1 时公式也成立。步骤如下：
假设n = m 时公式成立，即 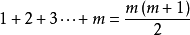（等式1）
然后在等式两边同时分别加上m + 1 得到 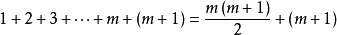（等式2）
这就是n = m+1 时的等式。我们下一步需要根据 等式1证明 等式2 成立。通过因式分解合并，等式2的右边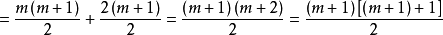
也就是

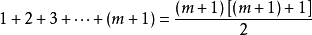
这样我们就完成了由n=m成立推导出n=m+1成立的过程。

结论： 对于任意自然数n，等差数列公式均成立。

引用自“科普中国”https://baike.baidu.com/item/%E6%95%B0%E5%AD%A6%E5%BD%92%E7%BA%B3%E6%B3%95/5155524?fr=aladdin

二分法的对数推导

分析：二分查找在最坏的情况下依次是n/2, n/4, n/8 … 1 为止
条件：意思就是要循环多少次才能查找到目标数呢，我们假设是x次
然后我们可以观察到分母是每次都乘以1/2，分子不变，所以可以根据题意列出下面等式：
第一步：n(1/2)x = 1
第二步：

第三步：

第四步：

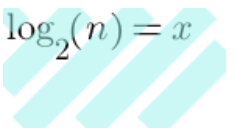
第五步： 依据大O推导公式，省略了常数列——log的底数（可看log2 => lg推导）

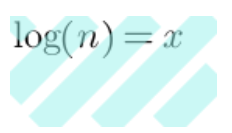
时间复杂度常规比较

公式： O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n3)<O(2^{n)//2的n方<O(n!)<O(n}n)//n的n方
曲线图：

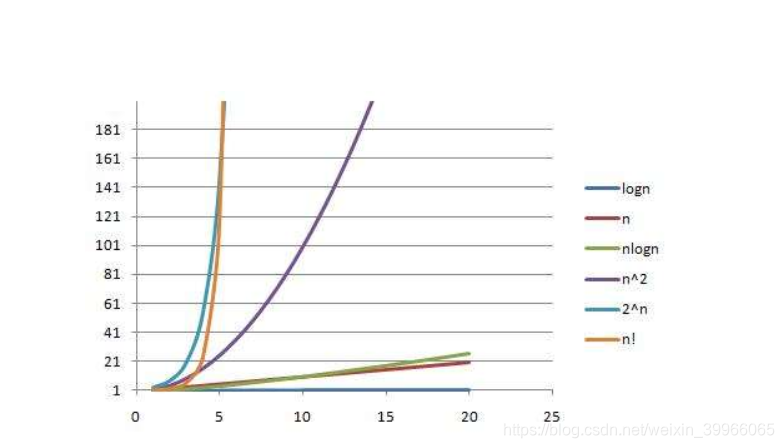
快速查询的时间复杂度推导

大概推论： 将 n 个数据划分为 n 个子序列，需要 logn 次，每次进行的数据移动次数是 n ， 所以为 nlogn

对数

对数的由来

由于没有计算器的帮助，想要算出几个很大数字的乘积，往往需要耗费大量的时间。对数的出现大大减少了计算乘积所需的工作量

例子：
x=567.89×3141.59两边同时取以10为底的对数，得到：log10(x)=log10(567.89×3141.59)=log10(567.89)+log10(3141.59)log10(x)=log10(10^2×5.6789)+log10(10^3×3.14159)log10(x)=2+log10(5.6789)+3+log10(3.14159)=5+log10(5.6789)+log10(3.14159)其中log10(5.6789)和log10(3.14159)可以在对数表中查出，把它们相加之后，再查反对数就能得到最终结果

对数的定义

1、求出2的多少次方才会等于8，我们可以用对数来表示这个数，即log2(8)，其结果就是log2(8)=3

2、用更一般的表达式来表示指数函数N=a^x，写成对数形式x=loga(N)（这里需要满足a>0，且a≠1）
a叫做对数的底数，N叫做真数，x叫做“以a为底N的对数”

3、指数和对数互为逆运算

log2^n ===> lgn 推导

转换公式：logb(a)=lga/lgb
log2^n = lgn/lg2
log2^n * lg2 = lgn 对数表：
lg5=0.6990
lg3=0.4771
lg2=0.3010

相关的数学公式了解

1、“∈”是属于符号，“⊆”是包含于符号，“⊇”是包含符

2、∑ “西格玛”是希腊字母
也有念作“西玛”“希玛”等各种读法，符号是∑,英文译音是Sigma, 表示数学中的求和号，是数学中常用的符号，主要用于求多项数的和，用∑表示
详细：
下面的小字,如i=1表示从i=1开始求和
上面的小字，如n表示求和到n为止
例子：
比如下面写i=1，上面写n，后面写xi(i是下角标)
表示从x1+x2+…+xn
例如1+2+3+4+…+100=5050可以写成