tar.gz压缩文件在linux上解压异常问题:gzip:stdin:invalid compressed data
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.rhkb.cn/news/498354.html
如若内容造成侵权/违法违规/事实不符,请联系长河编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
UE5材质节点CameraDepthFade
相机深度消失,Fade Length相机离物体位置,Fade Offset消失偏移 可以让物体随着相机距离消失
相机深度消失 边缘自发光
Python机器学习笔记(十五、聚类算法的对比和评估)
用真实世界的数据集对k均值、凝聚聚类和DBSCAN算法进行比较。
1. 用真实值评估聚类
评估聚类算法对真实世界数据集的聚类结果,可以用调整rand指数ARI和归一化互信息NMI。
调整rand指数 (adjusted rand index,ARI)和归一化互信息…
SAP PP bom历史导出 ALV 及XLSX 带ECN号
bom总数 104W PS超过XLSX上限 ,那就分文件 *&---------------------------------------------------------------------*
*& Report ZRPT_PP_BOM_HIS_ECN
*&---------------------------------------------------------------------*
*& tcode:zpp0…
《代码随想录》Day20打卡!
《代码随想录》二叉树:二叉搜索树的最近公共祖先
本题的完整题目如下: 本题的思路如下: 1.之前写过一个二叉树的最近公共祖先,本题相比于另一道题,不同是本题是二叉搜索树,有一些可用的性质。 2.本题使用递…
初识MySQL · 库的操作
目录
前言:
增
有关编码
删
查
改 前言:
由前文可得,MySQL是目前主流的数据库,mysql是客户端,mysqld是一种网络服务,mysqld是一种数据库服务,而对于数据库来说,是一种存储数据…
Idea创建JDK17的maven项目失败
Idea创建JDK17的maven项目失败 Error occurred during initialization of VM Could not find agent library instrument on the library path, with error: Can’t find dependent libraries Possible solution:
Check your maven runner VM options. Open Maven Runner setti…
优化租赁小程序提升服务效率与用户体验的策略与实践
内容概要
在这个快速发展的商业环境中,租赁小程序成为了提升服务效率和用户体验的重要工具。通过对用户需求的深入挖掘,我们发现他们对于功能的便捷性、响应速度和界面的友好性有着极高的期待。因此,针对这些需求,完善租赁小程序…
基础数据结构--二叉树
一、二叉树的定义
二叉树是 n( n > 0 ) 个结点组成的有限集合,这个集合要么是空集(当 n 等于 0 时),要么是由一个根结点和两棵互不相交的二叉树组成。其中这两棵互不相交的二叉树被称为根结点的左子树和右子树。
如图所示&am…
shell学习变量(二)
这里写目录标题 一、概念1、环境变量2、本地变量3、系统变量 二、环境变量三、本地变量四、系统变量五、定义变量规则1、命名规则2、定义方式3、unset命令:删除变量 一、概念
1、环境变量
环境变量指的是再当前进程有效,并且能够被子进程调用ÿ…
自动驾驶3D目标检测综述(六)
停更了好久终于回来了(其实是因为博主去备考期末了hh)
这一篇接着(五)的第七章开始讲述第八章的内容。第八章主要介绍的是三维目标检测的高效标签。 目录
第八章 三维目标检测高效标签
一、域适应
(一)…
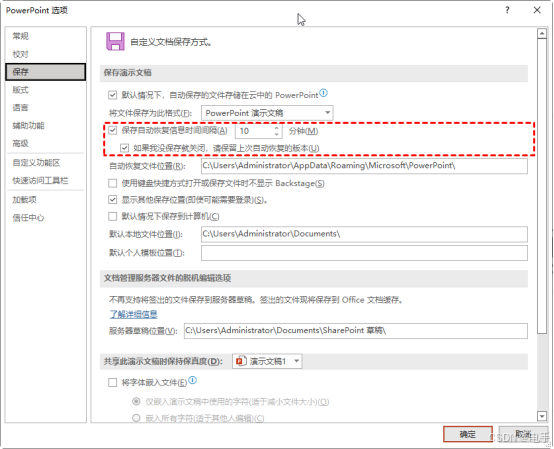
如何恢复永久删除的PPT文件?查看数据恢复教程!
可以恢复永久删除的PPT文件吗?
Microsoft PowerPoint应用程序是一种应用广泛的演示程序,在人们的日常生活中经常使用。商人、官员、学生等在学习和工作中会使用PowerPoint做报告和演示。PowerPoint在人们的学习和工作生活中占主导地位,每天都…
四大自平衡树对比:AVL树、红黑树、B树与B+树
AVL树、红黑树、B树和B树的对比与应用场景 树系列相关文章(置顶) 1、从链表到平衡树:二叉查找树的退化与优化 2、自平衡二叉查找树:如何让二叉查找树始终保持高效 3、AVL树入门:理解自平衡二叉查找树的基础 4、红黑树全…
IOS safari 播放 mp4 遇到的坎儿
起因
事情的起因是调试 IOS 手机下播放服务器接口返回的 mp4 文件流失败。对于没调试过移动端和 Safari 的我来说着实费了些功夫,网上和AI也没有讲明白。好在最终大概理清楚了,在这里整理出来供有缘人参考。
问题
因为直接用 IOS 手机的浏览器打开页面…
Kubernetes Gateway API-2-跨命名空间路由
1 跨命名空间路由
Gateway API 具有跨命名空间路由的核心支持。当多个用户或团队共享底层网络基础设施时,这很有用,但必须对控制和配置进行分段,以尽量减少访问和容错域。
Gateway 和 Route(HTTPRoute,TCPRoute,GRPCRoute) 可以部署到不同的命名空间中,路由可以跨命名空间…
第十六届蓝桥杯模拟赛(第一期)(C语言)
判断质因数 如果一个数p是个质数,同时又是整数a的约数,则p称为a的一个质因数。 请问2024有多少个质因数。 了解 约数,又称因数。整数a整除整数b,b为a的因数(约数)质数,又称素数。只有1和它本身两…
AI安全的挑战:如何让人工智能变得更加可信
引言 随着人工智能(AI)技术在各个领域的广泛应用,尤其是在医疗、金融、自动驾驶和智能制造等行业,AI正在重塑我们的工作和生活方式。从提高生产效率到实现个性化服务,AI带来了前所未有的便利。然而,在享受这…
TiDB 的MPP架构概述
MPP架构介绍: 如图,TiDB Server 作为协调者,首先 TiDB Server 会把每个TiFlash 拥有的region 会在TiFlash上做交换,让表连接在一个TiFlash上。另外 TiFlash会作为计算节点,每个TiFlash都负责数据交换,表连接…
springboot499基于javaweb的城乡居民基本医疗信息管理系统(论文+源码)_kaic
摘 要 信息数据从传统到当代,是一直在变革当中,突如其来的互联网让传统的信息管理看到了革命性的曙光,因为传统信息管理从时效性,还是安全性,还是可操作性等各个方面来讲,遇到了互联网时代才发现能补上自古…
【SQL Server】教材数据库(1)
1 利用sql建立教材数据库,并定义以下基本表:
学生(学号,年龄,性别,系名)
教材(编号,书名,出版社编号,价格)
订购(学号…
推荐文章
- JSP住宅小区物业管理系统(源代码+开题报告+论文+答辩PPT)
- GPT-4 发布:在考试中击败 90% 的人类;谷歌开放大语言模型 PaLM API;FireFox 111 发布|极客头条...
- html.parser --- 简单的 HTML 和 XHTML 解析器
- 软考-高级-系统架构设计师教程(清华第2版)【第6章 数据库设计基础知识(234~262)-思维导图】
- (C)1005 继续(3n+1)猜想
- (C语言)编写程序将一个4×4的数组进行顺时针旋转90度后输出。
- (javaweb)mysql---DDL
- (Python) Python语音处理工具包AudioSegment的基本使用
- (React Hooks)前端八股文修炼Day9
- (八)Flask之app.route装饰器函数的参数
- (二)pytest自动化测试框架之添加测试用例步骤(@allure.step())
- (泛型+栈+队列+可变不可变)的实现(java版)