着色(Shading)
- 可视性 / 遮挡
- Z - 缓冲 (Z - buffering,深度缓冲)
- 着色
- 光照 和 着色 (illunmination & Shading)
画家算法(Painter 's Algorithm)
先注明一下,这里的画家指的是油画家。画家算法的提出主要是为了实现深度缓冲
画家在画油画是,总是会从远景开始画,然后逐渐画近景覆盖远景,比如下图:最先画出一个蓝色的山,然后接着画绿地覆盖蓝色的闪,然后再接着画上几棵树覆盖绿地。

参考这个画家算法,我们要在图形学中画一个正方形就要如下的步骤:

先画出最后面的那个面,然后再画左面和下面,之后再画上面和右面,最后画正面。就可以得到这样一个正方体。先画背面最后画正面可以理解,那么四个侧面的顺序是如何决定的?目前我们只是暂时用这种画法,没有什么特殊的决定方法。但是若更改一下顺序,先画上面和左面,再画右面和底面,就会导致右面有一条线无法被覆盖,立方体的上面就会多出一条线。
按照画家算法的思想,要先对三角形的深度进行排序(O(nlogn)),排完序之后再按照从深到浅的顺序画三角形。但是这样实际应用的时候就会有问题,如下图:

你无法对这三个三角形按照深度的顺序进行排序。
深度缓冲(Z - Buffer / Depth Buffer)
z缓冲是当前使用较多的深度测试的方法,先声明一些问题:由于Camera是放在坐标原点指向-z轴(屏幕里面的),那么一个物体的z的坐标越小,这个物体离我们就越远;z的坐标值越大,离我们就越近。但是这里我们计算物体所处的深度时不这么取值,因为深度只能是一个大于0的数,所以我们取z的绝对的作为一个物体的深度。
其思想是:
- 对于每一个像素,我们存在一个当前最小的|z|作为这个像素绘制的物体的深度
- 需要一个额外的缓冲来记录每一个像素的深度值(|z|)
- 帧缓冲(frame buffer)存储每一个像素的颜色的值(color values)
- 深度缓冲(z - buffer)存储每一个像素的深度值
z - buffer的例子

如上所示,需要两个缓冲,一个缓冲存储最终的渲染效果,而另外一个z - buffer则用来存储每个像素的深度值。在深度图像上,一个像素的深度值越大,那么该点就会越白,如果深度值越小,该点就会越黑。(为什么?当取色范围为0-1时,color = 0为黑色,color = 1为白色,深度越小,对应的颜色值就越小,反应到图像上就是越黑,反之越白)在渲染中深度缓存是怎么工作的?我们可以单看一个像素点,比如立方体的左上角的点,我们在绘制图像时,先在该像素点上绘制了一个地板的颜色,然后在绘制立方体时,发现立方体的深度值比地板的深度值要小,那么就在这个像素点上绘制立方体的颜色来覆盖地板。
深度缓冲的算法(Z - Buffer Algorithm)

先把所有像素的深度值都初始化为无限大,然后对于每个三角形而言,对于三角形上的每一个像素点,如果这个像素点的深度值小于深度缓冲中的深度值,在该像素点绘制三角形的rgb颜色,然后更新深度缓冲的深度值为当前绘制的三角形的在该点的深度值;否则就什么都不做。
用图像来说明就如下:

上面仅代表深度图,而不是最后的成品图,其中R代表无限大。
为了实现z - buffer , 图形学中通常采用的做法是:在渲染最后成品图的同时,也会同时生成另外一个深度图像,这个深度图像只存储了任何一个像素他所看到的几何物体中最浅的深度信息。
深度缓冲的时间复杂度(Z - Buffer Complexity)
- 对于n个三角形而言,其时间复杂度为O(n)
- 因为这个算法并没有对三角形进行排序之类的工作,只是对在每一个像素上进行了一个判断,如果深度值小就写入,如果深度值大就什么也不做。比如说有三个覆盖100个像素的三角形,对这三个三角形所作的工作就是将其深度值与深度缓存比较,一个一个像素填入,所做的操作次数就是 3 * 100。所以时间复杂度其实就是 = 三角形的个数 × 每个三角形覆盖的像素的数。是一个O(n)的时间复杂度。
如果按照不同的顺序,用z - buffer 进行绘制三角形,会有什么效果?
结果不变,z - buffer 只记录了深度,和绘图的顺序没有关系。
接下来是新课内容:
着色(Shading)
- 光照和着色(illumination & Shading)
- 图形渲染管线(Graphics Pipeline)
我们到目前位置做了什么?

我们现在空间中拜访物体(Modeling transform,左上),然后将相机变换到原点的位置,并且旋转其指向方向(viewing transform, 右上);然后在相机的角度,对物体进行投影到屏幕上(projection transform,左下);最后进行光栅化,将物体绘制在屏幕上(右下)。
看一个例子:

根据目前我们所学习的内容,我们可以做出这样的一系列的立方体,但是看上去并不像我们平时所观察的立方体,得不到我们想要的效果,而我们想要的效果如下:

就可以发现,两幅图中,相差的效果就是光照。
但又不是单纯的只缺少了光照,现实生活中,不同的物体,因为物体的材质不同,对于光照的表现效果也是不同的。

着色(Shading)
着色的定义:通过平线性或者色块在图中引入不同的明暗和颜色。

Shading在图形学中定义是:对不同的物体用不同的材质进行着色
一个简单的着色模型(Blinn - Phong Relectance Model)

光源在右上的方向,光源照亮了所有的茶杯,可以看到茶杯上有一些颜色不同的地方
- 可以看到茶杯上有一个高光(Specular highlights)
- 茶杯表面除了高光外,其余颜色变化并不剧烈的地方,我们称之为漫反射(diffuse reflection)
- 光源在右上,在茶杯的背面应该看不到这个光源,那么茶杯的背面应该是黑色。但是我们看到了这个茶杯的背面并不是黑色,也就是说有一些的光从茶杯的背面反射到了我们的眼里,那么这个点一定是接受到了光。但是这个点接受到的并不是直接光照,而是间接光照。比如说光找到墙上,墙面发生了一个漫反射将光反射到了桌面上,光再经过桌面的反射就能到茶杯的背面。假如说任何一个点都能够接收到来自环境的反射光,这个反射光就是环境关照(Ambient lighting)
计算某一着色点的光照
计算一个点的光照,需要的的输入有:
- 观察者的方向向量 (Viewer direction , v)
- 着色点所在表面的法向量(Surface normal , n)
- 光线照射的方向向量(Light direction , I)
- 着色点表面的一些参数(颜色,材质,反光度等)

光照具有局部性(Shading is Local)
没有阴影会产生 (Shading != Shadow)

上图的光源在图片的左上方,可以看到物体表面上具有反光,还有漫反射,物体的背面为黑色,但是地板上没有阴影。这里的着色能够得到的效果只有物体表面上的光照效果。
漫反射(Diffuse Reflection)
光照在射到一个平面上时,会均匀的向四面八方进行反射,我们称这种反射为漫反射。

漫反射与观察者的位置没有关系,引文漫反射是向四面八方均匀的反射光纤,所以观察者不管从什么角度观察,表面的颜色都是一样的。
物体接受光线能量的方式
在现实中,将一个物体放在一个光源下,若是物体的角度不同,则物体的明暗也会不一样。这是为什么?

可以看第一幅图,图中有六根光线,每一根光线代表着一股能量,如果物体表面和光线垂直的画,那么物体可以接收到所有光线的能量,
如果物体表面下旋转了一定的角度,这是物体表面只接收到了三根光线,所以物体的表面就暗一些。如果要把这种现象推广到某种理论上去,就是说物体表面的法线和光线的夹角决定了物体表面应该有多亮,这是通过观测得到的结论。
更科学的解释是这样的:首先考虑光是一道能量,这就说明我看到了一个物体就代表着这些物体接收到了一定量的能量。比如说用太阳能板接受太阳光,太阳能板越大,接收到的光照的能量就越多。如果要考虑一个着色点能接受多少能量,那么就要看这个着色点周围的单位面积能接受到多少能量,但是着色点周围的单位面积始终是不变的,那就要考虑法向量和光线的夹角。考虑一下下面的情景:为什么地球会有冬天和夏天,并不是因为夏天离太阳近一些,冬天离太阳远一些。其实是因为当北半球在夏天时,太阳对北半球的光线是一个直射的状态,这个光照几乎时垂直北半球,这就说明夏天和冬天区别就是看光线是否垂直于我们所处的地球表面,这也就解释了为什么北半球是夏天时,而南半球是冬天,当光线直射北半球的时候,就不能直射南半球,南半球单位面积接收的光线的能量也就更少。
所以在图形学中,一个着色点附近的单位面积接受到的光线的能量是和光线的入射方向有关的。计算从不同角度接受到的光线能量有一个
Lambert’s cosine law(兰伯特余弦定理)。这个定理是说,接收到的光线的能量和 cos(光线的方向,着色点的法向量)的值 成正比。
当光线垂直于物体表面时,物体表面所能够接收到的光线的能量最大,而当光线垂直于物体的表面的法向量时,物体表面就不能接收到光线的能量,也就会非常暗。
光衰减(Light Falloff)
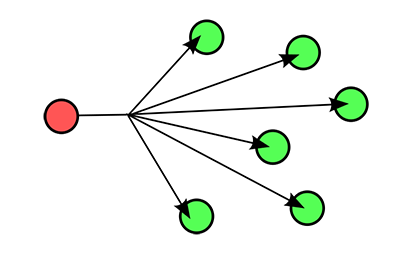
设想一下我们有一个如下图所示的点光源,朝四面八方发射光能量。

我们假设上图中的光是在真空中传播,光在传播过程中没有能量的损失。我们以球壳的方式来表现光向外发射能量的过程,即在某一时间点上,所有光线的终点可以围城一个球体。
由于光线在传播过程中没有能量损失,那么在每一个球壳上的能量的大小应该是相同的,即在靠近光源的一个小的球壳上所包含的光的能量应该是和外面的大的球壳上所包含的光的能量是相同的。
按照途中所示,我们假设在半径为1的这个球壳上所蕴含的能量为k,而在这个球壳上的每一点的光的强度是I,那么在半径为r的球壳上,在这个球壳上的光线的强度就应该是 I/(r*r)。
所以这就解释了为什么距离越远,光照的强度越弱。
漫反射的强度计算(Lambertian (Diffuse) Shading)
给定一个点光源,光线的方向向量I,着色点表面的法向量n,观察者的方向向量v,光线的入射角度θ,计算的方法如下:

我们之前已经得到:
- 着色点接受能量大小和 cos<I , n>的值成正比
- 光的强度在空间中的衰减程度
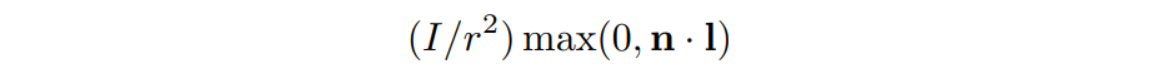
这两个相乘得到的就是 光线照射到着色点上时,着色点周围的单位面积所接收到的能量。至于这里的max函数的解释:因为当I和n的方向相反时,得到的结果为负数,这是什么意思,就是说光线穿过了物体
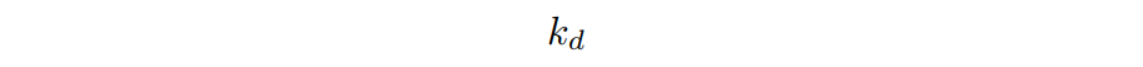
kd是一个系数,代表的是一个物体本身的颜色,或者是材质。因为不同的材质和光线作用的结果不同,所以还要再×这个系数。

漫反射的效果,kd从左往右依次增大