1. build DKTree

递推创建Tree；当前维度找中位数分割 数据集 left set，Node(mid), right set.

* 循环维度（当log(Nsample)>featureSize)

2. DKTree KNN search

* 理论部分向量几何有介绍。

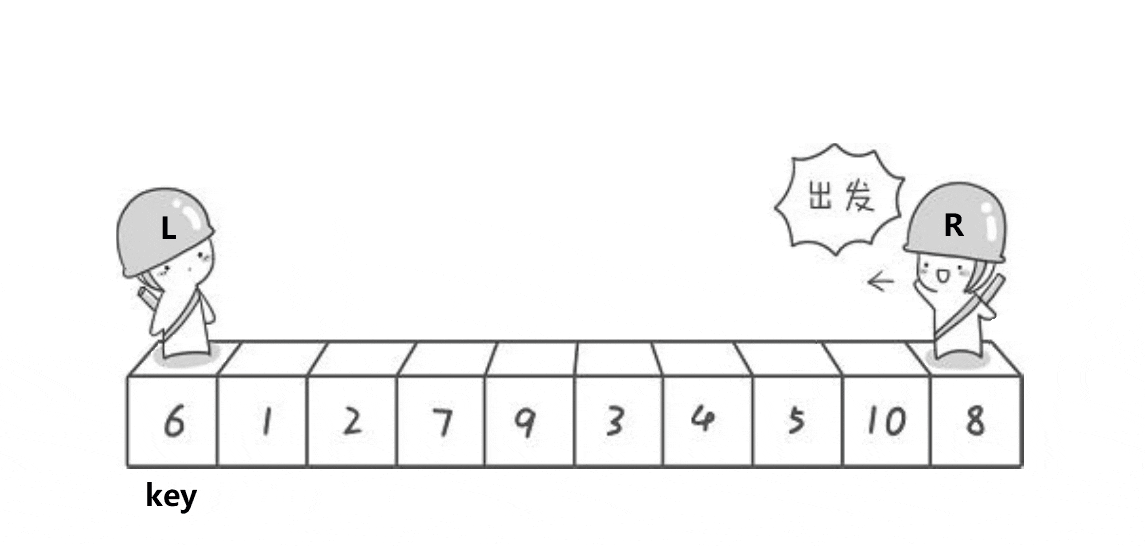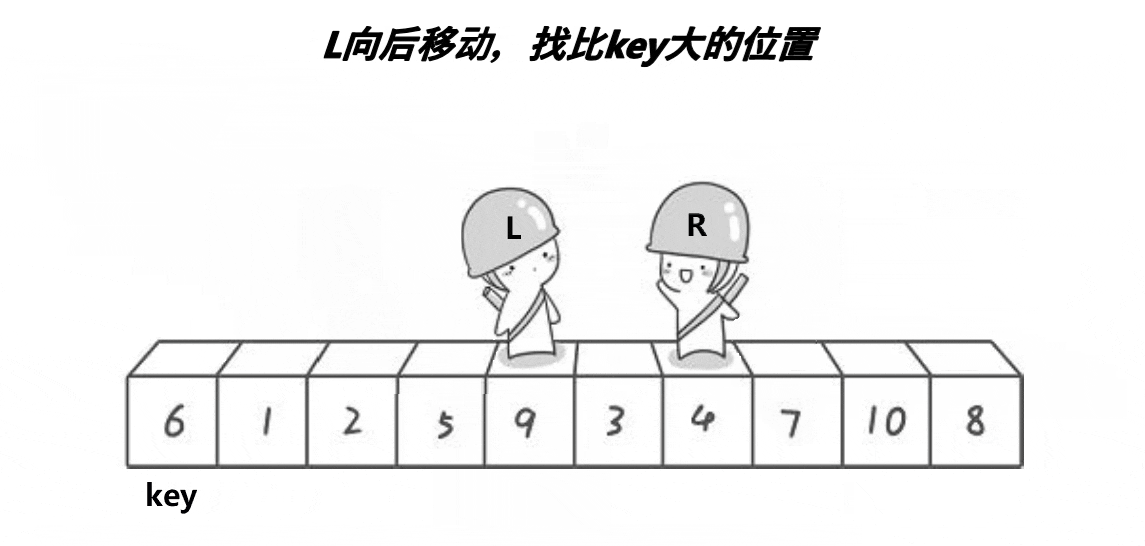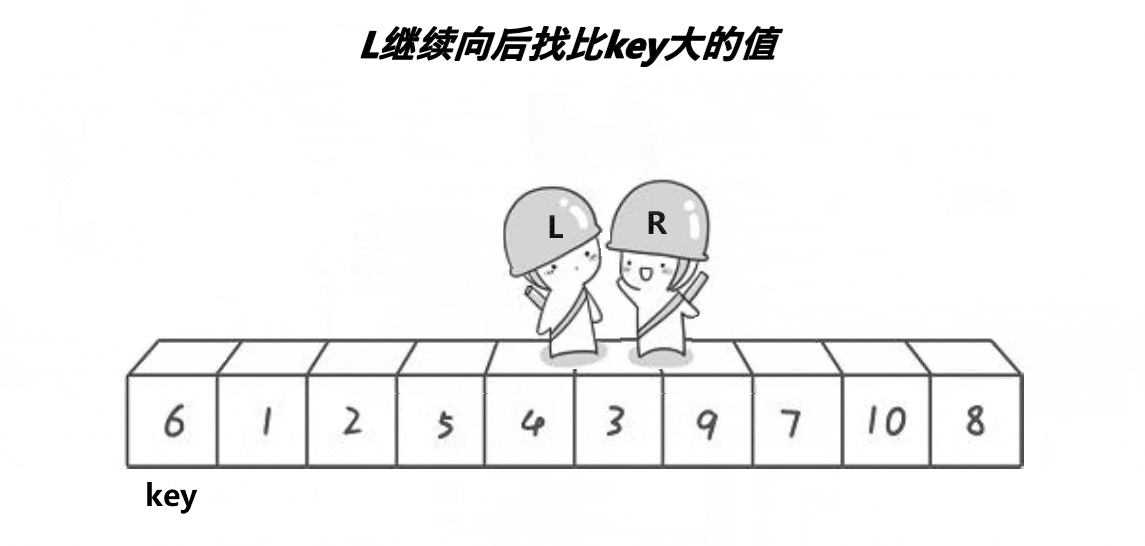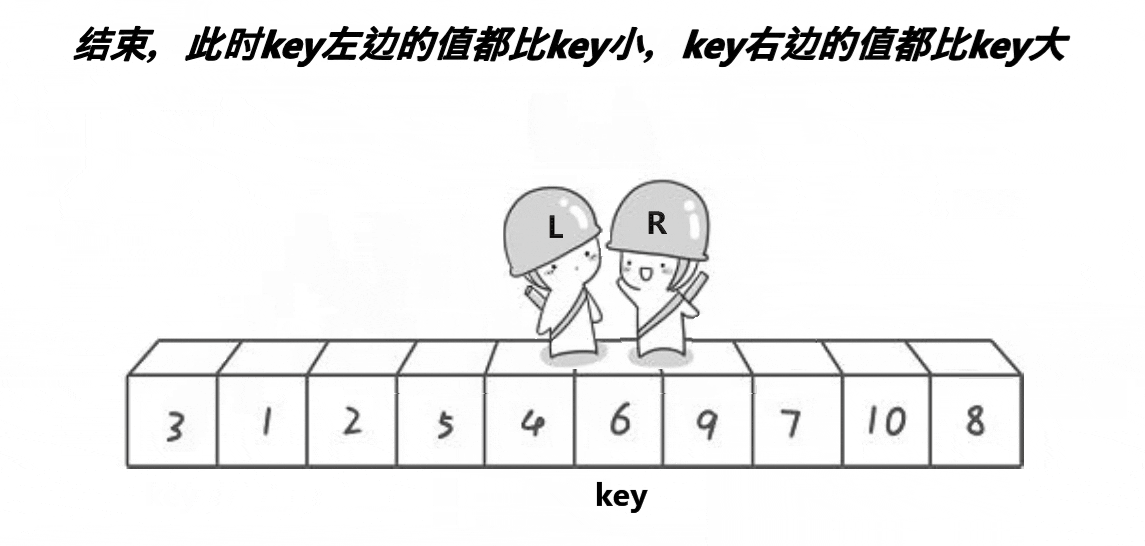
每个维度列中，中位数对应的数据点 X[i]在这个分割超平面上，其他数据是对应数据点到这个超平面的垂直距离；这个分割期望是只用继续搜寻leftNode or rightNode(而不用全部）

   - 当目标点的最大球 <= 目标点到当前维度的分割超平面的最小距离；即球体与超平面不相交。这时可以只用搜索2个子节点中的1个。

    *rightNode 中任意点x 到 leftNode中任意点y 的距离 一定大于 x到分割超平面的距离

     leftset  mid  rightSet 

     mid  rightSet 最短距离： A=(R[fi] - mid[fi]) = ((R[fi] - mid[fi]) ^2)^1/2 >=0

     leftset rightse  任一right点的距离： B= ((L[fi] - R[fi])^2 + (L[fj] - R[fj])^2 + ... )^1/2

            R[fi] < mid[fi] <  L[fi]   

      =>  R[fi] -L[fi] >= R[fi] - mid[fi]    

      => (L[fi] - R[fi])^2 >= (R[fi] - mid[fi])^2

      => (L[fi] - R[fi])^2 + alpha  >= (R[fi] - mid[fi])^2   | alpha >=0

      => (L[fi] - R[fi])^2 + (L[fj] - R[fj])^2 + ...  >= (R[fi] - mid[fi])^2

      => B >=  A

  

   * fi轴时，法向量为  V=（0，0，0，1,  0,  0,  0, ...)  | V[fi] = 1;

     mid超平面 H: f = { V dot Mid = Mid[fi] }

     =>  H [f:Mid[fi]]

3. 代码实现

//教程有完整的代码

参考资料：《Python机器学习》