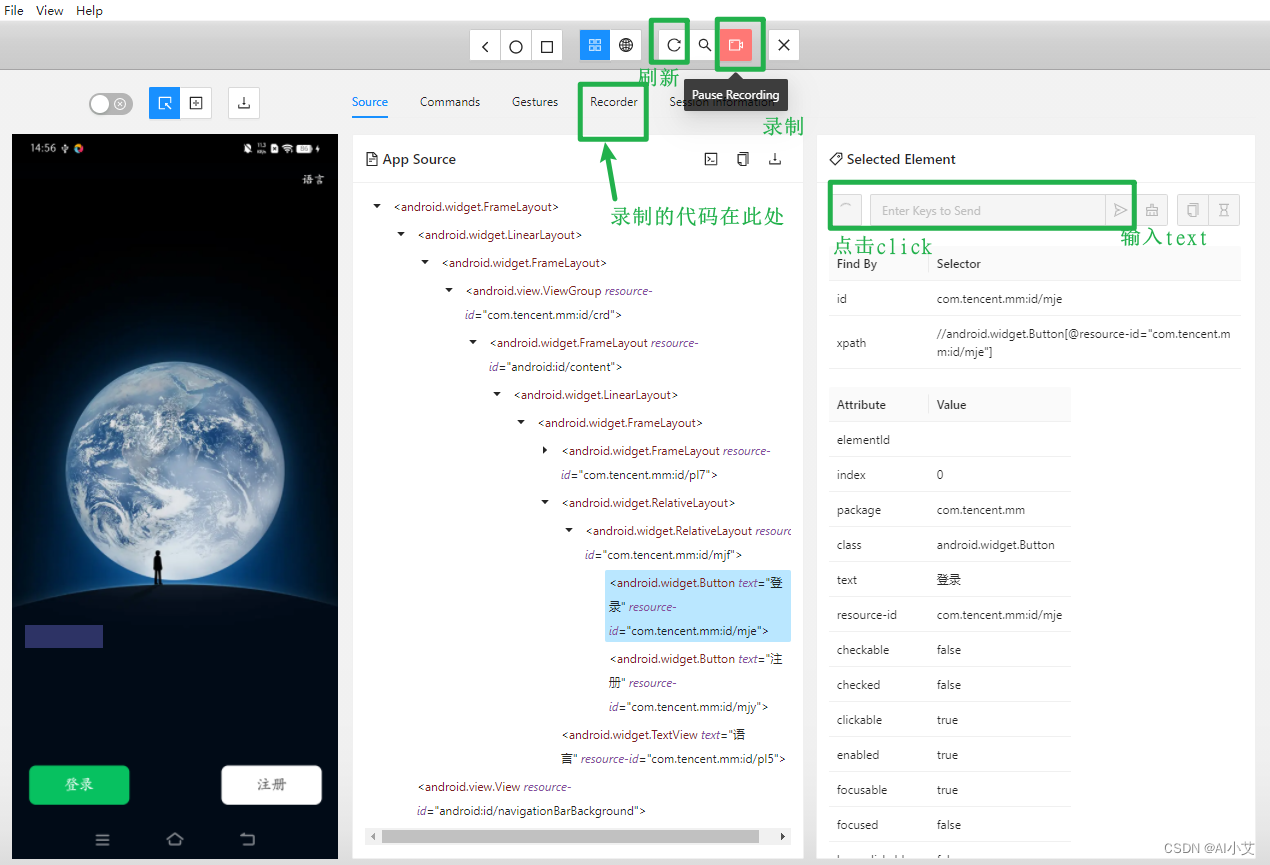
线性回归、逻辑回归算法应用请参考:
https://codeknight.blog.csdn.net/article/details/135693621
https://codeknight.blog.csdn.net/article/details/135693621本篇主要介绍决策树、随机森林、KNN、SVM、Bayes等有监督算法以及无监督的聚类算法和应用PCA对数据进行降维的算法的基本原理及应用。
目录
一、Decision Trees(决策树)算法建模及应用
决策树的优点主要包括:
决策树的缺点有:
决策树模型的两种规范(criterion)形式是基尼指数(gini)和熵(entropy):
应用案例——鸢尾花类别分类
1、导入函数库
2、加载数据集
3、划分特征集和响应集
4、划分训练集和测试集
5、加载决策树算法模型
5.1应用决策树模型的基尼指数(gini)规范建模
5.2模型性能评估
5.3决策树图像
5.4应用决策树模型的熵(entropy)规范建模
5.5模型性能评估
5.6决策树图像
二、Random Forests(随机森林)算法建模及应用
以下是随机森林算法的一些主要优点:
然而,尽管随机森林有许多优点,但也存在一些缺点:
应用案例(一)——鸢尾花数据集分类(随机森林处理离散型数据)
1、导入函数库
2、加载数据集
3、划分特征集与响应集
4、划分训练集和测试集
5、模型训练与预测
6、模型评估
7、模型预测
常用技巧1:特征变量权重分析 Feature_Importances_
1、计算权重占比
2、绘制权重占比图像
3、缩减特征变量X(对于成百上千特征变量的大数据集有非常重要的意义)
应用案例(二)——预测汽油的消耗量(随机森林处理连续型数据)
1、加载数据集
2、划分特征集和响应集
3、划分训练集和测试集
常用技巧2:Feature Scaling(特征缩放/标准化)
4、 训练模型与预测
5、模型评估
常用技巧3:调参
直观显示参数与误差之间的关系(寻找一个误差y最小时的参数x)
三、K Nearest Neighbour(KNN最近邻)算法建模及应用
求空间距离的算法总结:
求距离的详细公式:
应用案例——鸢尾花数据分类
1、导入数据集
2、 划分特征集和响应集
3、创建模型评估得分
4、调整模型参数K
5、绘制k与score的图像
常用技巧1:Grid search on KNN classifier
处理过拟合可以采取以下策略:
常用技巧2:Using RandomizedSearchCV
处理过拟合可以采取以下策略:
四、Support Vector Machine(支持向量机)算法建模及应用
应用案例(一)——SVM 对于 Iris 数据集的处理
1、导入函数库
2、加载数据集
3、数据集预处理
4、绘制数据图像
5、建立SVM模型并训练
6、获取模型参数,求出decision boundary和margin
7、绘制分类图像
8、调整参数C控制正则化强度
应用案例(二)——SVM 对于 弯月数据集的处理
1、加载数据集
2、绘制数据图像
3、数据标准化
4、模型训练
5、调参数C
6、支持向量机模型
案例应用(三)——SVM 对于 direct marketing campaigns (phone calls)数据集的处理
1、加载数据集
2、数据分析
3、实现数据类型转换——map()函数
4、实现数据类型转换——get_dummies()函数
5、划分训练集和测试集
6、模型训练
五、Bayes(贝叶斯)算法建模及应用
贝叶斯定理与公式
举例理解贝叶斯公式
贝叶斯的分类
(1)伯努利朴素贝叶斯
(2)多项式朴素贝叶斯
(3)高斯朴素贝叶斯
贝叶斯应用
应用案例(一)——)应用Gaussian Naive Bayes预测沉船存活人数
1、导入数据集
2、数据预处理
常用技巧1:数据类型转换(object->number)
3、划分训练集与测试集
4、模型训练
5、模型评估
6、模型优化
应用案例(二)——应用Multinomial Naive Bayes处理垃圾邮件
1、加载数据集
2、划分测试集和训练集
3、文本转向量
插曲:CountVectorizer 举例说明
4、模型训练
5、模型评估
插曲:Sklearn Pipeline 使用pipeline替代transform几行代码
六、K Means Clustering(K均值聚类)算法建模及应用
K-Means Clustering是什么?
K值应该怎样选取?
应用案例(二)——年龄与收入聚类分析
1、导入函数库
2、加载数据集
3、绘制数据图像
4、模型训练与预测
调参参考:Python在使用kmeans聚类函数时报错:AttributeError: ‘NoneType‘ object has no attribute ‘split‘_nonetype' object has no attribute 'split-CSDN博客
5、将分类添加到数据表格
6、打印聚类中心点坐标
7、绘制聚类散点图
常用技巧1:数据标准化
MinMaxScaler
Preprocessing using min max scaler
MinMaxScaler和StandardScaler的区别:
Elbow Plot
为什么选取Elbow Plot的突变点作为K?
应用案例(二)——KMeans clustering如何验证K点最佳 silhouette analysis(轮廓分析)
1、导入函数库
2、使用 yellowbrick 判断最佳K值
pip install yellowbrick