RC充电原理
下图是一个常见的RC充电电路:(假设R=10K,C=100nF)

- SW断开时,这个电路处于断路状态,C既没有充电也没有放电;
- SW闭合时,直流电源5V为电容C充电;
充电时电容两端的电压与电流分析
电压:SW刚刚闭合时,C两端的电压为0V,随着5V不断为C充电,C两端的电压不断增大,直到C充满电,即C两端电压为5V时充电完成停止充电;
电流:SW刚刚闭合时,充电电流最大为I=U/R=5V/10K=0.5mA,之后随着C左侧电压的升高,电流不断减小,直到C左端电压上升为5V时充电电流变为0,充电完成停止充电;
RC充电时间计算
t = R × C × ln e V 1 − V 0 V 1 − V t t=R\times C\times \ln_{e}{\frac{V1-V0}{V1-Vt} } t=R×C×lneV1−VtV1−V0
其中:
V1为电容能充到的最大电压;
V0为充电前电容两端的电压;
Vt为电容要充电达到的电压;
eg:电容从10%V1的电充到90%V1的电压所需要的时间为:
t = ∣ R × C × ln e V 1 − V 0 V 1 − V t ∣ = ∣ 10 k Ω × 100 n F × ln e V 1 − 0.1 × V 1 V 1 − 0.9 × V 1 ∣ = ∣ 1 × 1 0 − 3 × ln e 0.9 ∣ ≈ 1.053 m s t=\left | R\times C\times \ln_{e}{\frac{V1-V0}{V1-Vt} } \right | =\left | 10kΩ\times 100nF\times \ln_{e}{\frac{V1-0.1\times V1}{V1-0.9\times V1} }\right |=\left |1\times 10^{-3} \times\ln_{e}{0.9}\right | ≈1.053ms t= R×C×lneV1−VtV1−V0 = 10kΩ×100nF×lneV1−0.9×V1V1−0.1×V1 = 1×10−3×lne0.9 ≈1.053ms
另外还可以通过计算充放电时间常数来计算RC充满电的时间:
τ = R × C \tau =R\times C τ=R×C
电容电压从0V开始充电时,每经过一个充电时间常数,电容的电压增加待充电电压的0.632,电容的充放电曲线如下:


由上图可以看出,一般经过5个充放电时间常数的时间后,电容基本上已经从0-99%充满电或者从100%-1%放完电
RC充电电路仿真
普通充电电路的仿真结果

由上图仿真结果可以看出:
- 电压:电容两端的电压(蓝色线)由0V逐渐升高,直到充满电电容两端电压变为5V后稳定下来;
- 电流:流过电容C的电流(绿色线)与流过电阻R的电流(红色线)是一致的,开始时电流最大为5V/10K=0.5mA,之后充电电流逐渐减小,直到充电完成后一直保持为0;
- 充电时间:计算充放电时间常数为10K*100nF=1ms,经过5个充放电时间常数后即5ms后,电容C充电完成;
仿真结果与上面理论分析结果吻合;
变种一充电电路的仿真结果
变种一:在RC两端并联一个电阻进行仿真;

由上图仿真结果可以看出:
- 电压:电容两端的电压(蓝色线)由0V逐渐升高,直到充满电电容两端电压变为5V后稳定下来;
- 电流:流过电容C的电流(绿色线)与流过电阻R的电流(红色线)是一致的,开始时电流最大为5V/10K=0.5mA,之后充电电流逐渐减小,直到充电完成后一直保持为0;
- 充电时间:计算充放电时间常数为10K*100nF=1ms,经过5个充放电时间常数后即5ms后,电容C充电完成;
- 并联电阻R2电流:并联电阻的电流(浅蓝色线)一直为5V/10K=0.5mA;
- 并联电阻R2电压:并联电阻的电压(粉色线)一直为5V;
并联电阻R2两端的电压差一直为5V,流过并联电阻R2的电流也不变;
电容两端电压会在电容的充电过程中发生变化是因为电容上端电压一直为5V,下端在充电过程中有电流流过R1,R1上有一定压减,因此电容下端的电压发生变化,导致电容两端电压不断变化;
因此,RC两端并联一个电阻R2不会影响流过R1的电流也就不会影响到电容的充电过程;
仿真结果与上面理论分析结果吻合;
因此,变种一在RC两端并联电容并不会对充电电路造成影响;
变种二充电电路的仿真结果
变种二:在C两端并联一个电阻进行仿真;
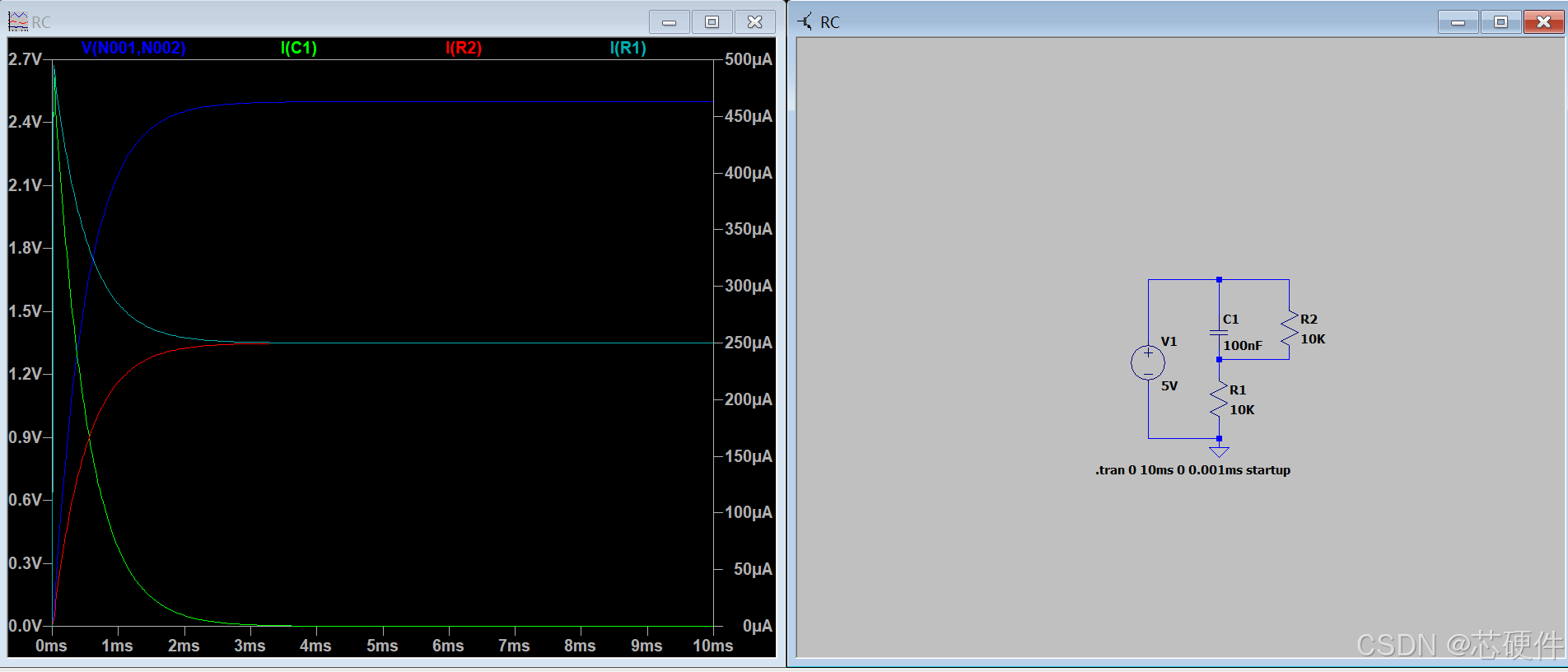
由上图仿真结果可以看出:
- 电压:电容两端的电压(蓝色线)由0V逐渐升高,直到充满电电容两端电压变为2.5V后稳定下来;
- 电流:流过电容C的电流(绿色线)开始时电流最大为5V/10K=0.5mA,之后充电电流逐渐减小,直到充电完成后一直保持为0;
- 充电电阻R1电流:并联电阻的电流(浅蓝色线)开始时电流最大为0.5mA,充电过程中持续减小,直到充电完成后一直保持为0.25mA;
- 并联电阻R2电流:并联电阻的电流(红色线)开始时为0,充电过程中持续增大,直到充电完成后一直保持在0.25mA;
- 并联电阻R2电压:并联电阻的电压与电容两端电压保持一致;
- 充电时间:大约经过2.5ms后,RC充电完成;
并联电阻R2两端电压与电容两端电压一致保持一致,开始时,电容两端电压为0,并联电阻两端电压也为0,因此开始时并联电阻两端流过的电流为0,之后不断为电容C充电,两端电压持续增大,因此并联电阻的电流也开始增大,直到电阻完全充满电,充满电后的稳定电压为2.5V(R1与R2分压),稳定后并联电阻的电流为2.5V/10K=0.25mA;
由于开始时并联电阻R2两端无压差,R2流过的电流为0,因此开始时5V先给电容充电,流过R1的电流为5V/10K=0.5mA,之后再充电过程中,电容两端电压增大,流过R2的电流增大,流过R1的电流减小;直到充电完成后,流过R1和R2的电流一致为5V/(10K+10K)=0.25mA;
在电容两端并联电阻时,电容实际充电电压会有所减少(因为R1与R2分压,C充满电时的电压有并联电容R2分压所得来决定),因此固定R1时,并联电容R2阻值越小,C充电所需要的时间越少;
仿真结果与上面理论分析结果吻合;
因此,变种二在C两端并联电容会减小电容充满电时的电压值,也会减少充满电所需的时间;