复旦大学2021机试

2021年真题

第一题

题目描述：给定一颗二叉树，树的每个节点的值为一个正整数。如果从根节点到节点 N 的路径上不存在比节点 N 的值大的节点，那么节点 N 被认为是树上的关键节点。求树上所有的关键节点的个数。请写出程序，并解释解题思路。
例子：
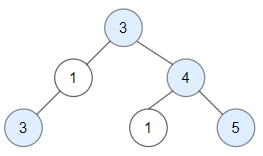
在这里插入图片描述
输入： 3, 1, 4, 3, null, 1, 5
输出：4（图中蓝色节点是关键节点）

解题：
思路如下：
1.用 A[maxv]数组表示树，则结点 i 的父亲结点是 i/2 向上取整。（null 的结点用 0 输入）
2.dp[i]表示从根结点到结点 i 的路径上最大的结点值。 ans 表示关键节点个数 //如果结点i 的值 A[i] 比从根结点到结点i 的父结点的路径上结点值 dp[i/2]都大，则是关键节点；反之，不是关键节点。

if (A[i]>=dp[i/2] ){dp[i]=A[i];ans++;
}else{dp[i]=dp[i/2];
}

测试用例：
一：输入： 3 1 4 3 0 1 5
输出： 4
//注： 4 个结点分别是： 3 4 3 5
二：输入： 4 5 2 1 3 4
输出： 3
//注： 3 个结点分别是： 4 5 4
三：输入： 3
输出： 1

//时间复杂度O(n)
#include<stdio.h>
const int maxn=10010;             //null的结点用0输入
int A[maxn],dp[maxn];             //A[maxn]是树的数组表示，dp[i]是从根节点到节点i的路径上最大的结点值int main(){int x,ans,num=0;            //ans记录关键节点个数while(scanf("%d",&x)!=EOF){   //树的数组表示A[++num]=x;}//边界for(int i=1;i<=num;i++){dp[i]=A[i];}ans=1;                         //根结点是关键节点//状态转移方程for(int i=2;i<=num;i++){if(A[i]>=dp[i/2]){         //节点i的值 比 从根节点到节点i的路径上节点值 都大，所以是关键节点dp[i]=A[i];ans++;}else{                     //非关键节点dp[i]=dp[i/2];}}printf("%d",ans);return 0;
}

#include<iostream>
using namespace std;
const int maxn=10010;             //null的结点用0输入
int A[maxn],dp[maxn];             //A[maxn]是树的数组表示，dp[i]是从根节点到节点i的路径上最大的结点值int main(){int x,ans,num=0;            //ans记录关键节点个数while(cin>>x){   	//树的数组表示A[++num]=x;}//边界for(int i=1;i<=num;i++){dp[i]=A[i];}ans=1;                         //根结点是关键节点//状态转移方程for(int i=2;i<=num;i++){if(A[i]>=dp[i/2]){         //节点i的值 比 从根节点到节点i的路径上节点值 都大，所以是关键节点dp[i]=A[i];ans++;}else{                     //非关键节点dp[i]=dp[i/2];}}cout<<ans;return 0;
}

第二题
题目描述：训练场上有一个台阶，总共有 n 级。一个运动员可以跳 1 级，也可以跳 2 级。求运动员有多少种跳法。请写出程序，并解释解题思路。

解题:
思路如下：动态规划
dp[i]是 i 级台阶的跳法数。dp[i]可以从dp[i-1]跳一步得到和从dp[i-2]跳两步得到，递推边界 dp[1]=1， dp[2]=2。

测试用例：
一：输入： 3；输出： 3
二：输入： 4；输出： 5
三：输入： 5；输出： 8

//时间复杂度 O(n)
#include<stdio.h>
const int maxn=10010;
int dp[maxn]={0};      //dp[i]是i级台阶的跳法数int main(){int n;scanf("%d",&n);//边界dp[1]=1;        dp[2]=2;//状态转移方程//不断递推得到dp。dp[i]可以从dp[i-1]跳一步得到和从dp[i-2]跳两步得到for(int i=3;i<=n;i++){dp[i]=dp[i-1]+dp[i-2];}printf("%d",dp[n]);return 0;
}

第三题
题目描述：给定一个非负整数序列x1,x2,x3…xn，可以给每一个整数取负数或者取原值，求有多少种取法使得这些整数的和等于期望值E。请写出程序，并解释解题思路。
输入：1, 1, 1, 1, 1, 3
输出：5

样例解释:

-1+1+1+1+1 = 3
1-1+1+1+1 = 3
1+1-1+1+1 = 3
1+1+1-1+1 = 3
1+1+1+1-1 = 3

#include<iostream>
#include<map>
#include<vector>
#include<numeric>
using namespace std;int main(){cout<<"输入序列（-1为结束符）："<<endl;vector<int> nums;while(1){                   //输入序列（以-1为结束符）int x;cin>>x;if(x==-1) break;nums.push_back(x);}int sum=accumulate(nums.begin(),nums.end(),0);      //序列和int n=nums.size();                                  //序列个数cout<<"请输入期望值E："<<endl;int E;cin>>E;//边界vector<map<int,int> > dp(n+1);                      //v可以为负值，考虑用 vector<map<int,int>>进行解决   for(int i=0;i<=n;i++){for(int v=-sum;v<=sum;v++){if(i==0 && v==0) dp[i][v]=1;else dp[i][v]=0;}}//状态转移方程for(int i=1;i<=n;i++){for(int v=-sum;v<=sum;v++){//dp[i][v]=dp[i-1][v-nums[i-1]]+dp[i-1][v+nums[i-1]]//即前i个值取到v的方法数 = 前i-1个数取到 v-nums[i-1]的方法数  +  前i-1个数取到 v+nums[i-1]的方法数 （注意nums[i-1]是第i个数）int temp1,temp2;if(v-nums[i-1]>=-sum) temp1=dp[i-1][v-nums[i-1]];if(v+nums[i-1]<=sum)  temp2=dp[i-1][v+nums[i-1]];dp[i][v]=temp1+temp2;}}cout<<dp[n][E];return 0;
}