一.汉诺塔问题

1.汉诺塔问题的来源

源自古印度的汉诺塔游戏，具体相传来源，可自行搜索

2.汉诺塔问题的意义

有人觉得，汉诺塔是一个非常无聊的问题，只有一个盘子的时候，直接移动就完成了，两个盘子的时候也只是稍微多了2次，三个盘子的时候也仅较两个盘子多移动了4次…
这样下去，无论你是10个盘子，还是20个盘子，总能在经过一定移动次数过后完成目标，那这样你是否会觉得很无聊？这有什么用呢？为什么还是有那么多人去想着用各种各样的方式去解决它？

究其原因（浅显理解），我认为有一下几点：
1.锻炼脑力，考验耐性
2.理解递归、栈等重要应用

3.汉诺塔游戏规则

该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置N个盘子。

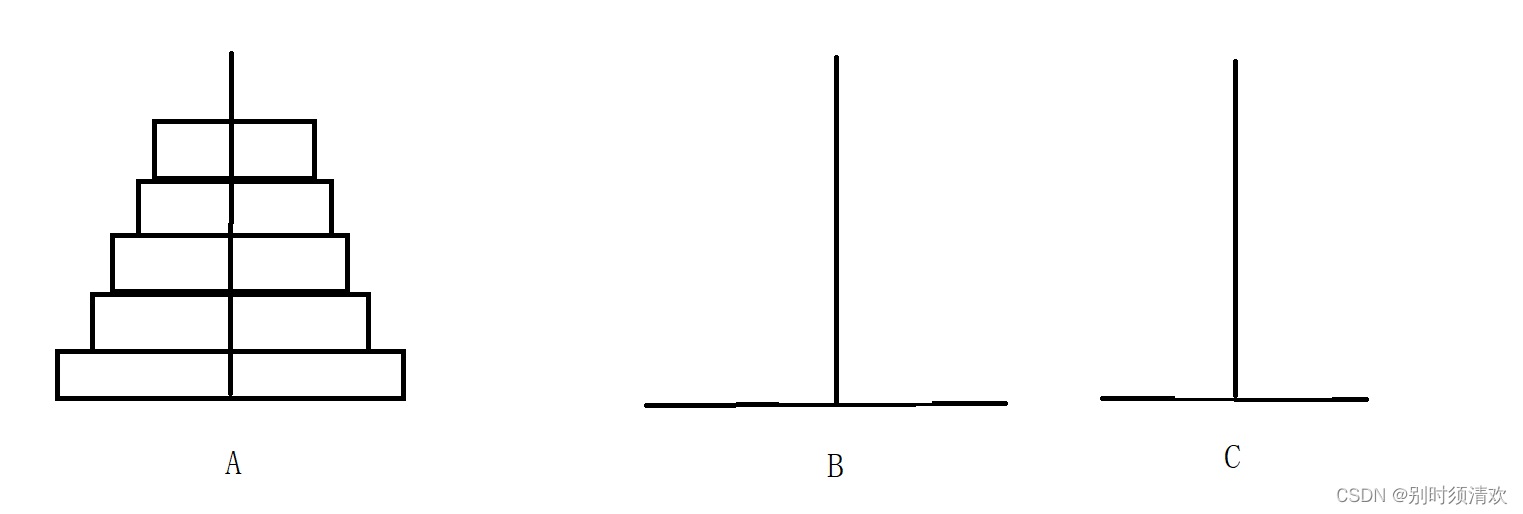
游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。

操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

二.代码实现

1.问题分析

对于汉诺塔问题，该怎样去理解呢？
1.N=1,一个盘子的时候，我们只需要移动一次，直接将其从A上移动到C上
2.N>=2,两个以上盘子的时候，我们只需要将N-1个盘子借助C先移动到B，在将A中第N个盘子移动到C（如下图）

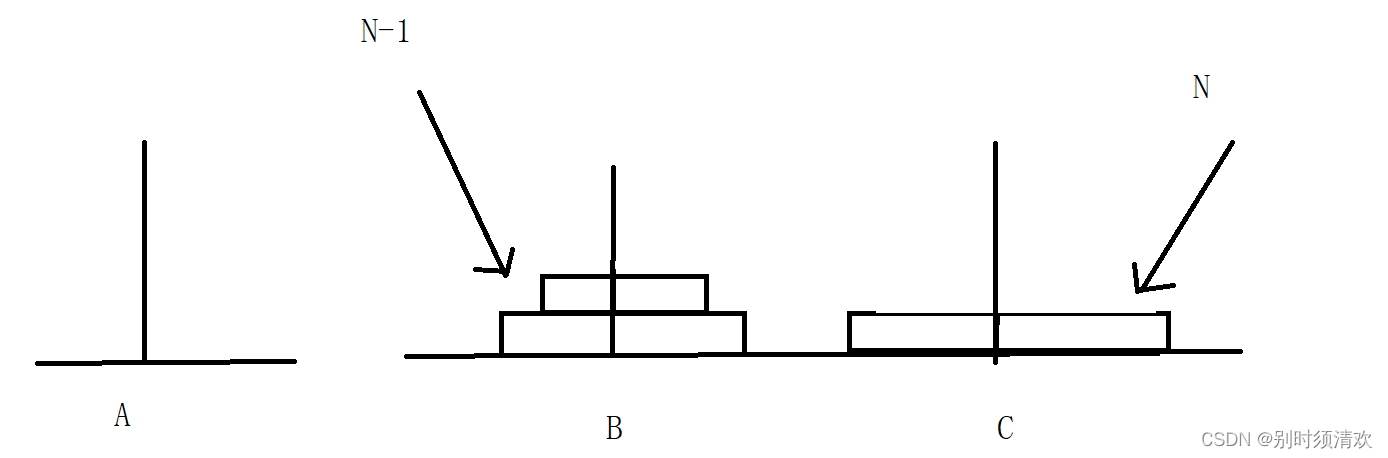
3.当N移动到C上后，此时A上没有盘子，可以作为我们N-1个盘子中把第N-2个盘子通过A中转挪到C上的桥梁。
4.当第N-1个盘子移动到C上后，此时B上没有盘子，可以作为N-2个盘子中第N-3个盘子通过B移动到C上的桥梁

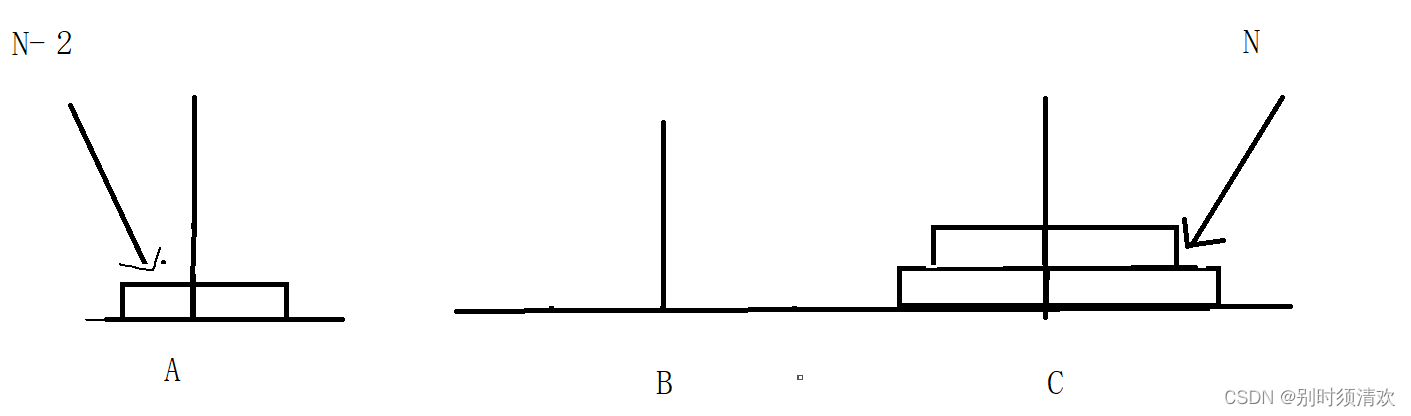
5.如此往复，通过A,B两根柱子的中装，直至将所有的盘子全部按照规则挪到C上

通过上面的分析，不难发现这是一个对于同一件事情不断反复操作，即将N-1个盘子通过B©中转直至都挪到C上，与递归的思想一致，因此，解决上述问题，我们可以采用递归的方法

2.代码实现

C语言实现：

//A - 起始位置
//B - 中转位置
//C - 目标位置
#include<stdio.h>
int count = 0;
void hanoi_tower(int n, char dest1, char dest2, char dest3)
{if (n == 1){printf("第%d次：%c->%c ", ++count, dest1, dest3);}//里面即为完成将N-1个盘子中的第N-1个盘子从A移动到Celse{//将n-1个盘从A通过C移动到Bhanoi_tower(n - 1, dest1, dest3, dest2);printf("第%d次：%c->%c ", ++count, dest1, dest3);//将n-1个盘子从B通过A移动到Chanoi_tower(n - 1, dest2, dest1, dest3);}
}int main()
{int n = 0;scanf("%d", &n);hanoi_tower(n, 'A', 'B', 'C');printf("一共移动了%d次", count);
}

运行结果如下：

JAVA实现：

/*  dest1--起始位置
*   dest2--中转位置
*   dest3--目标位置
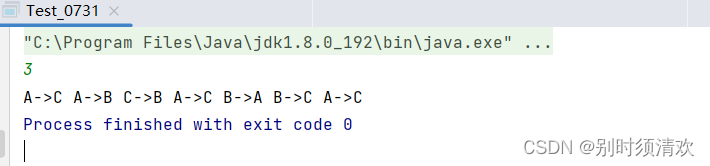
* */public static void hanoi_tower(int n, char dest1, char dest2, char dest3) {if (n == 1) {move(dest1, dest3);return;} else {//1.把n-1个盘 从dest1借助dest3放到dest2上hanoi_tower(n - 1, dest1, dest3, dest2);//2.将dest1上最地下那个盘从dest1直接放到dest3上 完成将最大得先放在目标中move(dest1, dest3);//3.把dest2上得n-1盘从dest2借助dest1放到dest3上 完成整个挪动hanoi_tower(n - 1, dest2, dest1, dest3);}}//模拟盘子移动public static void move(char dest1, char dest2) {System.out.print(dest1 + "->" + dest2 + " ");}//经典汉诺塔问题public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();hanoi_tower(n, 'A', 'B', 'C');}

运行结果如下：

三.汉诺塔问题总结

汉诺塔问题是需要预先计划和回顾性计划，非常的考研耐性和逻辑规划，在递归解决汉诺塔问题中，最主要的是有一个整体性的思想，将除了N个盘子中，第N个盘子以外的N-1个盘子当作整体移动即可，把N-1个盘子、N-2个盘子的移动看作是一个问题（将A中的盘子挪到C上）的子问题（将N-1个盘子借助B或者A中转挪到C上）