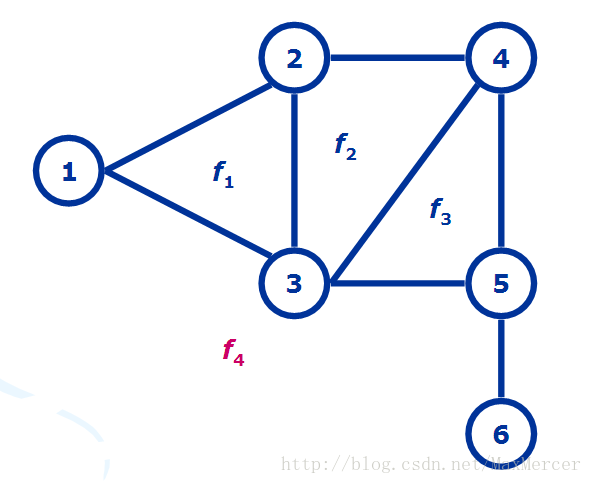
平面图定义:
图存在一种形式,所有的边只在顶点处相交,那么这个图就是平面图。
对偶图定义:
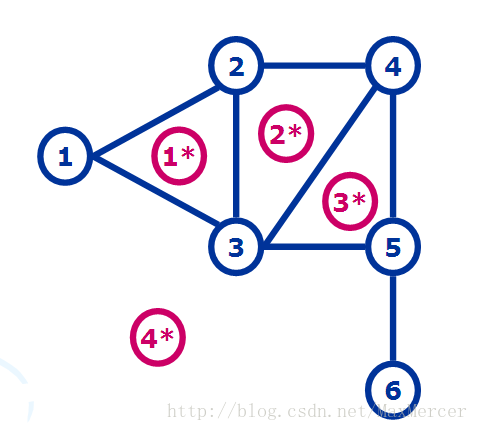
对于每一个平面图, 都有与其相对应的对偶图. 我们假设上面的例图是图G, 与其对应的对偶图G*, 那么对于G*来说, G*上面的每一个点, 对应的是G里面的每一个面. 比如说下面就是G*.
上面的点就是对偶图G里的点.
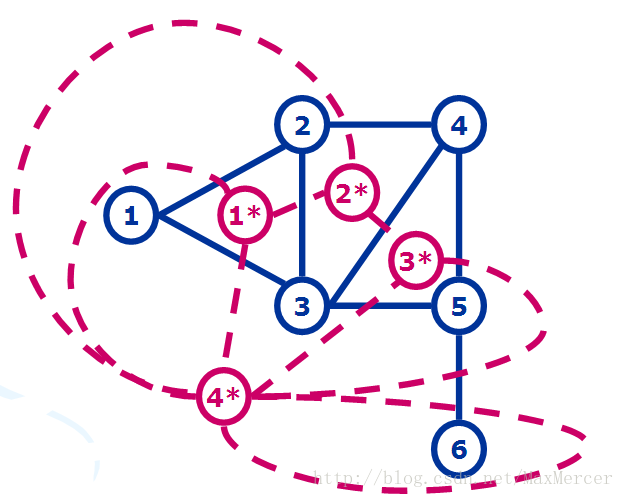
那么关于对偶图G*里的边呢 ? 对于G中本来的每条边e, 他是两个面(比如说面f1和f2)的交边, 那么在对偶图里, 我们对这两个面(f1, f2)所映射在G*里的点连线(f1* 连向f2*). 如果f1 == f2(比如说G中5, 6这条边, 边的两侧都是同一个面, 那我们就建一条回边.
图就长这样(回边在5, 6那里).
求网络流的最小割或最大流时,如果时平面图,就可以转化成对偶图,然后对对偶图求s',t'的最短路,就是原网络的最大流和最小割。就是对偶图的点需要自己对应好。。