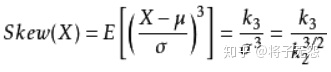SPSS：数据分析

1、数据采集

2、数据是否服从正态分布

3、T检验（T Test）

4、方差分析（ANOVA）

5、卡方检验（Chi-square Test）

6、灰色关联度分析（Grey Relation Analysis，GRA）

7、弗里德曼检验（Friedman Test）

8、箱图（Box）

1、数据采集

1、数据分类

定性	观察、访谈、调查
定量	手动测量、自动测量、问卷打分
主观	等级、排序、感觉、有用性
客观	时间、数量、错误率、分数
自变量	不同的实验条件因素，研究的因素
因变量	不同的实验条件所影响的、要观测的因素

连续数量值（preference）	时间、数量、错误率
离散数量值（usability	问卷打分
等级数量值（usability）	等级、排序

变量类型
Norminal Data 定类变量	变量的不同取值仅仅代表了不同类的事物，这样的变量叫定类变量。问卷的人口特征中最常使用的问题，而调查被访对象的“性别”，就是定类变量。对于定类变量，加减乘除等运算是没有实际意义的。
Ordinal Data 定序变量	变量的值不仅能够代表事物的分类，还能代表事物按某种特性的排序，这样的变量叫定序变量。问卷的人口特征中最常使用的问题“教育程度“，以及态度量表题目等都是定序变量，定序变量的值之间可以比较大小，或者有强弱顺序，但两个值的差一般没有什么实际意义。
Interval Data 定距变量	变量的值之间可以比较大小，两个值的差有实际意义，这样的变量叫定距变量。有时问卷在调查被访者的“年龄”和“每月平均收入”，都是定距变量。
Ratio Data 定比变量	有绝对0点，如质量，高度。定比变量与定距变量在市场调查中一般不加以区分，它们的差别在于，定距变量取值为“0”时，不表示“没有”，仅仅是取值为0。定比变量取值为“0”时，则表示“没有”。

2、数据采集方法

客观数据避免引入人为误差；根据实际环境和需求确定；问卷调查需要注意方法、形式；加标签等管理方法避免混乱

问卷星：设计问卷，可以在线完成基本的数据分析，也可以和spss相关联进行分析。

问卷网

3、数据分析软件

excel：各条件下观测量的均值、方差、标准误差

Spss：整体的单因素ANOVA分析和两两之间post-hoc分析，获得对应自由度下的比对结果（F,p）

4、数据分析方法

怎么判别我的数据中存在特异值？教你几招！

异常值处理方法
保留异常值	采用非参数Friedman test检验; 用非最近端的值代替极端异常值(如用第二大的值代替极端异常值); 因变量转换成其他形式; 将异常值纳入分析，并坚信其对结果不会产生实质影响。
剔除异常值	直接删除异常值很简单，但却是没有办法的办法。当我们需要删掉异常值时，应报告异常值大小及其对结果的影响，最好分别报告删除异常值前后的结果。而且，应该考虑有异常值的个体是否符合研究的纳入标准。如果其不属于合格的研究对象，应将其剔除，否则会影响结果的推论。

具体参照师兄的HCI实验数据分析之数据可靠性计算，绘制箱图，描述性变量统计，ANOVA,Bonferroni 的连续变量方差分析

5、数据分析目的

评价观测变量的效果如何

检验实验条件下的观测变量是否与对比条件有显著区别

2、数据是否服从正态分布

1、什么样的数据应该满足正态分布

数据类型
连续数据	时间、身高、年龄（可以无限限划分）	需要正态分布，用于后期参数检验（先假设H0，根据检验结果作出拒绝或接受假设H0的判断）	F检验（ANOVA） T检验卡方检验 Bonferroni检验
离散数据	评分（只能是1、2、3等整数）	非参数检验（无法对总体分布形态作简单假设）	卡方检验二项分布检验 K-S检验 Friedman检验变量值随机性检验等

数据类型

连续数据

时间、身高、年龄（可以无限限划分）

需要正态分布，用于后期参数检验（先假设H0，根据检验结果作出拒绝或接受假设H0的判断）

F检验（ANOVA）

T检验

卡方检验

Bonferroni检验

离散数据

评分（只能是1、2、3等整数）

非参数检验（无法对总体分布形态作简单假设）

卡方检验

二项分布检验

K-S检验

Friedman检验

变量值随机性检验等

针对连续数据的分析，我们同样应该明白一个概念，假设实验中为什么要进行假设？

假设是为了设定一个衡量标准，通过计算出统计量是否满足一个阈值，来证明你的结果是否和假设一致。

2、为什么要判断数据是否符合状态分布

简单来说，状态分布是最简单的判断数据是否有问题的方法；如果不符合状态分布，一般的F检验、T检验或其它统计分析方法将会失效

3、如何判断一组数据是否符合正态分布

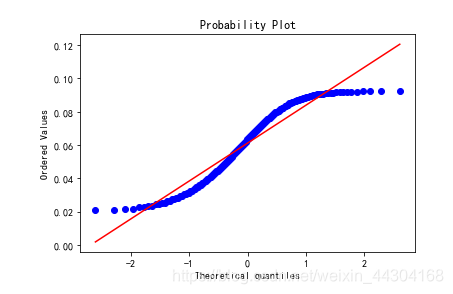
描述统计方法（用描述的数字或图表来判断数据是否符合正态分布）	Q-Q图	Q是quantile的缩写，即分位数。分位数就是将数据从小到大排序，然后切成100份，看不同位置处的值。比如中位数，就是中间位置的值。 Q-Q图的x轴为分位数，y轴为分位数对应的样本值。x-y是散点图的形式，通过散点图可以拟合出一条直线，如果这条直线的斜率为标准差，截距为均值.，则可以判断数据符合正态分布，否则则不可以。如果拟合出来的直线是45度，可以保证中位数两边的数值分布是一样的，即正态分布中基于中位数左右对称。 SPSS软件实现实例
	P-P图	P-P图是根据变量的累积概率对应于所指定的理论分布累积概率绘制的散点图，用于直观地检测样本数据是否符合某一概率分布。如果被检验的数据符合所指定的分布，则代表样本数据的点应当基本在代表理论分布的对角线上。 P-P图的检验原理与Q-Q图基本相同，只是Q-Q图用的是分布的分位数来做检验，而P-P图是用分布的累计比。和Q-Q图一样，如果数据为正态分布，则在P-P正态分布图中，数据点应基本在图中对角线上。 SPSS软件实现实例
	直方图	直方图分为两种，一种是频率分布直方图，一种是频数分布直方图。频数就是样本值出现的次数，频率是某个值出现的次数与所有样本值出现总次数的比值。从直方图我们可以很直观的看出这组数据是否符合正态分布。 SPSS软件实现实例
	茎叶图	茎叶图的思路是将数组中的数按位数进行比较，将数的大小基本不变或变化不大的位作为一个主干（茎），将变化大的位的数作为分枝（叶），列在主干的后面，这样就可以清楚地看到每个主干后面的几个数，每个数具体是多少。可以看作事数据化的直方图
统计检验方法	SW检验	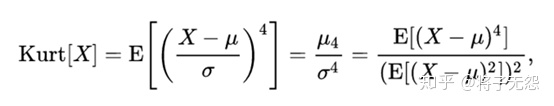S：偏度（skewness），是统计数据分布偏斜方向和程度的度量，是统计数据分布非对称程度的数字特征。包括右偏分布（也叫正偏分布，其偏度>0），正态分布（偏度=0），左偏分布（也叫负偏分布，其偏度<0）。公式左1。 W：峰度（kurtosis），表征概率密度分布曲线在平均值处峰值高低的特征数。直观看来，峰度反映了峰部的尖度，计算方法为随机变量的四阶中心矩与方差平方的比值。公式上就是把偏度计算公式里的幂次改为4即可。峰度包括正态分布（峰度值=3），厚尾（峰度值>3），瘦尾（峰度值<3）。公式左2。 SPSS软件实现实例
	KS检验	KS检验是基于样本累积分布函数来进行判断的。可以用于判断某个样本集是否符合某个已知分布，也可以用于检验两个样本之间的显著性差异。如果是判断某个样本是否符合某个已知分布，比如正态分布，则需要先计算出标准正态分布的累计分布函数，然后计算样本集的累计分布函数。两个函数之间在不同的取值处会有不同的差值。我们只需要找出来差值最大的那个点D。然后基于样本集的样本数和显著性水平找到差值边界值(类似于t检验的边界值)。判断边界值和D的关系，如果D小于边界值，则可以认为样本的分布符合已知分布，否则不可以。
	AD检验	AD检验是在KS基础上进行改造的，KS检验只考虑了两个分布之间差值最大的那个点，但是这容易受异常值的影响。 AD检验考虑了分布上每个点处的差值。
	W检验	W检验(Shapiro-Wilk的简称)是基于两个分布的相关性来进行判断，会得出一个类似于皮尔逊相关系数的值。值越大，说明两个分布越相关，越符合某个分布。

3、如何将非正态分布数据转换成正态分布

数据不符合正态分布怎么办？？？别着急，可以进行数据转换，使其满足正态分布。

	原始数据X（必须为正值），变换后数据X’	应用场景
对数变换	X’=lgX 当原始数据中有小值及零时，亦可取X’=lg（X+1）还可根据需要选用X’=lg（X+k）或X’=lg（k-X）	（1）使服从对数正态分布的数据正态化。如环境中某些污染物的分布，人体中某些微量元素的分布等，可用对数正态分布改善其正态性。（2）使数据达到方差齐性，特别是各样本的标准差与均数成比例或变异系数CV接近于一个常数时。
平方根变换	X’=sqrt（X）	（1）使服从Poission泊松分布的计数资料或轻度偏态资料正态化，可用平方根变换使其正态化。（2）当各样本的方差与均数呈正相关时，可使资料达到方差齐性。
倒数变换	X’=1/X	常用于资料两端波动较大的资料，可使极端值的影响减小。
平方根反正弦变换	X’=sin-1sqrt（X）	常用于服从二项分布的率或百分比的资料。一般认为等总体率较小如＜30%时或较大（如＞70%时），偏离正态较为明显，通过样本率的平方根反正弦变换，可使资料接近正态分布，达到方差齐性的要求。

SPSS软件实例演示：SPSS实践笔记：将非正态分布数据转换为正态分布。SPSS软件正态转换实例

数据满足正态分布之后，我们就可以进行后续的参数检验了。

师兄的spss数据处理整理

3、T检验（T Test）

T检验是平均值的比较方法。需要假设再论证。

SPSS官方教程：SPSS Paired Samples T-Test Tutorial

分类	定义	实例
单一样本T检验（One-Sample T Test）	用于比较一个正态总体在方差未知时总体均值与某一已知数是否有显著性差异。或者说，用看比较未知样本总体的均值和已知样本总体的均值（这个是已知的）是否有显著性差异。这里的单一样本是指只有一个样本总体。	选取了5个人，测定了他们的身高，要看这五个人的身高平均值是否高于、低于还是等于1.70m
独立样本T检验（Independent-Samples T Test）	用于检验两个独立样本是否来自具有相同均值的总体，本质是对两个样本均值之差进行T检验。	选取了5男5女，想看男女之间身高有无差异，这样，男的一组，女的一组，这两个组之间的身高平均值的大小比较可用这种方法。
配对样本T检验（Paired-Samples T Test）	用于检验两个配对总体的均值是否存在显著性差异。这里的配对是指，这两个样本值之间是一一对应的，样本容量相同。	选取了5个人，分别在饭前和饭后测量了他们的体重，想检测吃饭对他们的体重有无影响，就需要用这个t检验。注意，配对样本t检验要求严格配对，也就是说，每一个人的饭前体重和饭后体重构成一对。

t检验方法是由你的数据特点和你的结果要求来决定的。 t检验会计算出一个统计量来，这个统计量就是t值， spss根据这个t值来计算最终值sig值。

sig值的意思就是显著性（significance），即平均值是在百分之几的几率上相等的。

结果	结论	说明
sig值 > 0.05	两组数据差异不显著	说明平均值在大于5%的几率上是相等的，而在小于95%的几率上不相等。我们认为平均值相等的几率还是比较大的，说明差异是不显著的，从而认为两组数据之间平均值是相等的。
sig值 < 0.05	两组数据差异显著	说明平均值在小于5%的几率上是相等的，而在大于95%的几率上不相等。我们认为平均值相等的几率还是比较小的，说明差异是显著的，从而认为两组数据之间平均值是不相等的。

t检验的几种应用案例，T检验临界值表

4、方差分析（ANOVA）

又称“变异数分析”或“F检验”，用于两个及两个以上样本均数差别的显著性检验。

生物、化学中和人机交互（HCI）中的repeated measure one-way ANOVA（单因素重复测量方差分析）之间的区别

比如，评价AR系统相对于传统系统是否能显著改变时间

什么样的数据适合单因素方差分析：当我们看到这种要同时比较多组样本的均值时，首先就要想到one-way ANOVA，然后再想想用此检验方法是否真的合适。

单因素方差分析	对成组设计的多个样本均数比较，应采用完全随机设计的方差分析	单因素方差分析，和Excel示例，SPSS官网教程：SPSS One-Way ANOVA Tutorial
多因素方差分析	对随机区组设计的多个样本均数比较，应采用配伍组设计的方差分析	多因素方差分析(无重复试验双因素)，和SPSS程序实现

如何理解ANOVA中的F值与P值，方差分析（ANOVA）与f值，p值

F：越大，认为数值之间存在的差异就越大。

贼棒贼详细的教程，直接看这个就OK啦：SPSS：单因素重复测量方差分析（史上最详细教程）

这个太复杂，那就先看这个简单点的：单因素方差分析ANOVA及事后检验（这个是单因素，但是包含多个群组，分析群组之间的差异）

5、卡方检验（Chi-square Test）

卡方检验就是检验两个变量之间有没有关系。什么是卡方检验（这个链接说到很好很清楚）

比如，评价出错和AR/传统系统的关系

SPSS官方教程：SPSS Chi-Square Independence Test Tutorial

求卡方值
求自由度
先指定置信度	比如：95%

算出自由度和卡方值，根据界值表查询出理论置信度

指定置信度 > 理论置信度	认为假设不成立
指定置信度 < 理论置信度	认为假设成立

卡方检验实例，和界值表

卡方检验运用中常见的3大错误，来看实例！

X^2衡量理论与实际的差异程度

P：小于给定的阈值，相关性就越大

6、灰色关联度分析（Grey Relation Analysis，GRA）

是一种多因素统计分析的方法。

简单来讲，就是在一个灰色系统中，我们想要了解其中某个我们所关注的某个项目受其他的因素影响的相对强弱，再直白一点，就是说：我们假设以及知道某一个指标可能是与其他的某几个因素相关的，那么我们想知道这个指标与其他哪个因素相对来说更有关系，而哪个因素相对关系弱一点，依次类推，把这些因素排个序，得到一个分析结果，我们就可以知道我们关注的这个指标，与因素中的哪些更相关。

关注这一个博客案例就全明白了：灰色关联度分析（Grey Relation Analysis，GRA）原理详解