一、序言

    初次看到信息熵的公式有很多不理解的地方，只知道信息熵如何进行计算，却不懂得公式背后的原理，我通过查阅了一些资料，加深了对信息熵的理解，现在将这些理解分享给大家。如有疑问欢迎评论，若对你有帮助，麻烦点个赞。未经允许、请勿转载。（本文适合只知道信息熵的公式，但是不明白其中原理的人进行阅读）

二、什么是信息熵

    正如我们想要衡量某个物体的质量引入了克这个单位、我们想衡量时间，我们设计一秒钟这么长。香农老人家想要量化一条消息中带有的“信息量”的大小，提出了信息熵。
那么，首先明确一个问题，什么样的消息算作“信息量大”呢？什么样的消息又算作“信息量小呢”？举个例子昨天小明和我说：“今天罗志祥又和周扬青秀恩爱了！”，我就觉得这有啥的，他们天天秀恩爱。也就是说小明的这条消息并不能给我带来很大的信息量。
BUT今天小明和我说：”周扬青怒锤罗志祥!!!罗志祥人设崩塌！！！“，我就会很惊讶，因为这条消息给我的信息量很大。（类似的信息量很大的消息还有：小明告诉我今天太阳会从西边升起）
我们用信息熵来描述一个事件混乱程度的大小（一个事件我们一定知道结果，那么这个事件的混乱程度就是0；一个时间充满随机性，我们猜不到或者很难猜到结果，那么他的混乱度就很大）
引用下面一个在箱子里面摸球的例子，我们来更具体的了解信息熵。
（此例引自：Youtube的一个视频）

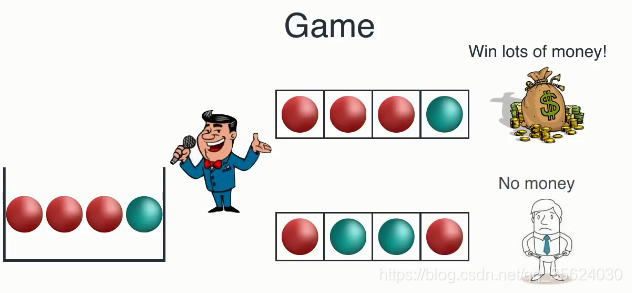
图左侧中有一个装有四个球的封闭箱子（这个箱子里面有三个红球、一个蓝球），现在我们从箱子中随机取出一个球，记录它的颜色后再放回箱子中，重复四次操作。如果你依次取出的序列为右上角所示（第一次取到红色、第二次取到红色、第三次取到红色、第四次取到蓝色），则你可以获得奖金；否则你就输了。大家用初中数学来算一算，我赢得奖金的概率是
$$P（x）=\frac{3}{4}\ast \frac{3}{4}\ast \frac{3}{4}\ast \frac{1}{4}=\frac{27}{256}$$
  现在明确了这个游戏的规则，那么我们分析一下如下几个箱子与赢得奖金的情况，分别计算一下获胜概率



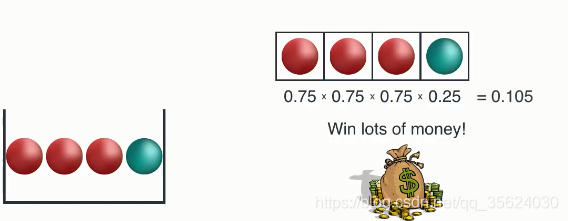
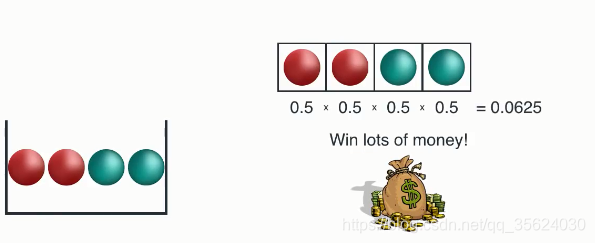
（每个图的左边是这个箱子的红球与蓝球初始条件，右侧是获胜所要求的序列，大家自己算算这个概率和图上写的一样吗？）

我们来分析一下这三种状态的游戏，第一次由于箱子内全是红球、该箱子的随机性很弱，也就是说还没摸我就知道结果了。这种状态带来的信息量很小；第三个箱子随机性很强，也就是说，对于结果我们充满未知。这个状态的信息量很大。我们算出的这个概率越接近1时候，这个信息熵应该越接近0；算出的这个概率越小的时候，信息熵反而应该越大。我们需要找到这么一个公式来满足这一点。（暂停思考一下，有哪些公式可以满足）
 该可以很轻松的想到，用刚才P（winning）的概率取倒数可以吗？ 答案是，只考虑刚才的问题，是可以的。但取倒数这个方式还是存在一些问题，比如第三个箱子取0.0625的倒数，算出来的这个信息量为16，如果这个P（winning）概率算出结果很小时，取倒数后就会变得非常大，所以我们认为这个乘法的规则并不是很好（换言之，我们希望曲线平滑一些）。香农发现log函数可以很好的解决这个问题。 因为log(a*b) = log(a)+log(b);而恰巧像抽箱子的独立事件P(AB) = P(A）*P（B）。【原因不止于此，后面我们还会再详细讨论】。
所以香农取了一个-log(x)这么一个函数来表示某一状态的信息量大小，因为x是概率事件取[0,1],所以log(x)是一个递增的恒负的值，取一个负号，-log(x)是一个恒正、递减的函数，正好符合我们的预期。

表的第四列就是我们用log计算出的结果。而我们刚刚是依次计算的每一个球的结果，为了表示系统的平均信息量。我们除4得到最终的信息熵。

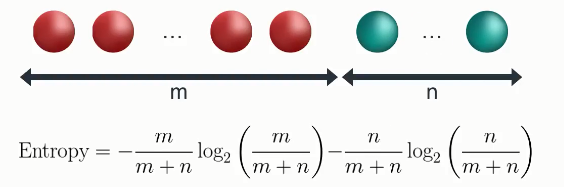
我们来将这个模型一般化，m个红球n个蓝球，信息熵表示如上图所示。
我们可以再将模型一般化一些，如果这个箱子里有多种不同颜色的球，我们就公式变成了如下的样子：
$$H_{(x)}=-\sum _{i=1}^n{P}_{(x_i)}\ast log(P(x_i))$$
这就是信息熵。也就是说，我们规定拿出一枚硬币，随意投出后，他可能是正面也可能是反面，它的信息熵是单位1（用刚才的方法来算算是不是1）。就像我们在这节开始所提到的，我们知道一个物体是几千克。是因为我们有一个1kg的砝码作为参考。我们能感受到时间流逝了多少秒，是因为我们规定了秒的单位。

三、为什么是log

 这章我们会再用一个例子来讲解，为什么是信息熵为什么要用log？还是以一个游戏为例。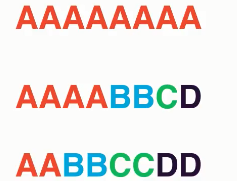
在上述的8个字母中，任取一个字母（我们不知道取的是什么，但我们知道初始的8个字母是什么），现在让你来猜这个字母是什么。
利用我们刚刚学过的信息熵，我们可以知道第一个序列的信息熵很低、第三个最高。我们可以计算出如下结果

（这个信息熵大家自己算一下，和上面计算的方式完全一样）
重点来了： 下面我们用一种提问的方式，来解决这个问题。你可以像系统提问（比如：这个字符是A吗？），系统会给你回答，你根据回答继续进行提问，直到猜到结果为止。以第二个序列为例；系统选了D，让你来猜。你会这样提问：
Q1：这个字符是A吗？ Answer：不是
你就知道，这个答案只能是B,C,D中的一个，你就会继续提问:
Q2：这个字符是B吗？ Answer：不是
你就会继续问：
Q3：这个字符是C吗？Answer：不是
好了，你不会再继续问下去了，因为这个答案一定是D。
也就是说通过这种方式，如果答案是A，你会猜1次，答案是B你会猜两次，答案是C或者D，你会猜三次。平均猜测次数为
$$E（x）=\frac{1}{4}\ast 1+\frac{1}{4}\ast 2+\frac{1}{4}\ast 3+\frac{1}{4}\ast 3=2.25次$$
显然，你可以选择一种更精妙的提问方式，来缩减平均猜测的次数
你可以这样进行提问：
Q1：这个字符是A或B吗？ Answer：不是
Q2：那么这个字符是C吗？ Answer：不是
好了，那么我知道这个字符是D了。也就是通过这种方式，我们不管是哪一个字符，我们只需要问两次就可以解决问题，我们用一种更直观的树来表示，如下图所示

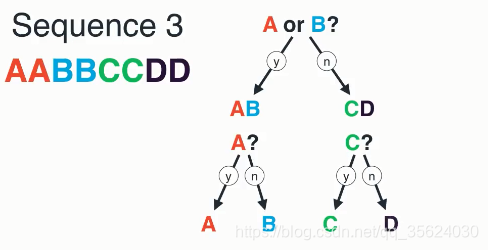
恰巧，这种提问二选一的过程，恰巧是个抛硬币的过程。由于我们类似的等价于抛了两次硬币，我们可以知道，这个过程的信息熵是2。我们再用信息熵的公式试一试
$$H（x）=\frac{1}{4}\ast log(4)+\frac{1}{4}\ast log(4)+\frac{1}{4}\ast log(4)+\frac{1}{4}\ast log(4)=2$$
（这里我们把符号直接化进log中了）

大家发现没有，log(x)是不是恰巧等于x需要询问的次数呢？！！！这也是这个公式的精妙所在，在离散数学中我们学过，一个树的高度等于log（节点数），这个log（x）恰巧是询问的高度，也就是投硬币的次数！这原来就是使用log的原因
上面的例子中A,B,C,D都是等概率出现的；下面我们将这个过程一般化，看一看当每个随机变量不等概率时的运算过程

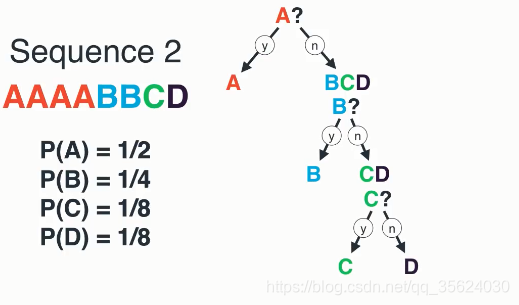
我们看如上的序列，其中A出现的概率要等于BCD之和。所以我们为了让我们的提问次数最小化，我们要尽力讲每次提问的YorN分成等概率，也就是我们要问的第一个问题是：
Q1:这个字符是A吗？
如果不是，我们知道是B,C,D但是B的概率等于C和D之和，我们就再问：
Q2:这个字符是B吗？
如果不是，这时候C和D等概率，我们随便问一个即可：
Q3：这个字符是C吗？
好了，现在得出了结论。
问出A需要1次，B2次，C和D都是三次。
我们用信息熵来计算一下。
$$H（x）=\frac{1}{2}\ast log(2)+\frac{1}{4}\ast log(4)+\frac{1}{8}\ast log(8)+\frac{1}{8}\ast log(8)$$
每一个log(x)恰巧对应着他所在的叶子在树的第几层，也就是他需要询问的次数，前面乘上一个概率，是不是发现这个公式提出的非常巧妙！！

同时，在二进制计算机中，一个比特为0或1，其实就代表了一个二元问题的回答。也就是说，在计算机中，对于这个事件进行编码，所需要的平均码长为H（x）个比特。

三、结语

 通过上述过程，相信大家能清楚的理解信息熵。本文并没有一些数学上详细的证明，暂时留个坑以后填。如果大家有什么问题，欢迎在评论区交流，如果觉得有用麻烦点个赞~
如果觉得还没看够，那不妨看看续集~：
KL散度、交叉熵——谈谈自己对信息熵的理解
参考资料：
[1]https://www.youtube.com/watch?v=ErfnhcEV1O8
[2]https://blog.csdn.net/v_JULY_v/article/details/40508465