【招商银行数据方向笔试题】—— 信用卡推荐客户列表

题目：
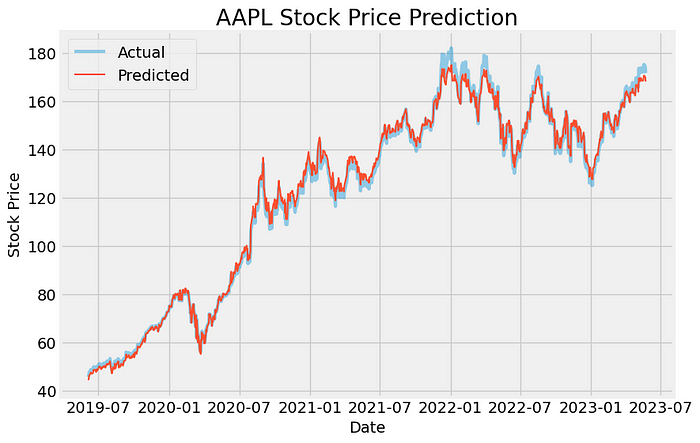
现在信用卡开展营销活动，持有我行信用卡客户推荐新户办卡，开卡成功后可获得积分奖励。规定每个客户最多可推荐两个新户且一个新户只能被推荐一次。但允许链接效应，即若客户A推荐了新户B，新户B推荐新户C，则客户C同时属于A和B的推荐列表。简单起见，只考虑以一个老客户A作起点推荐的情况。编程计算推荐新户数不小于n的客户列表。

输入示例：
5 2
A B C
C F *
B D E
D G *
E H I

输入描述：
输入的第一行为以空格分隔的两个正整数，第一个表示原始推荐列表的个数m，第二个表示n的取值。
其后m行每行均为一个以空格分隔的原始推荐列表，第一列为推荐人，后面两列为被推荐人，若该推荐人只推荐了一个新户，则第三列以*替代。推荐人和被推荐人均以大写字母表示，不同字母代表不同的人。

输出示例：
A B E

输出描述：
即在同一行输出符合条件的客户列表，无顺序要求，客户间以空格分隔。若客户列表为空，则输出None。

题目理解：
重点：链接效应——决定深度搜索的树结构
即：在以一个老客户A作为起点的推荐情况建立一棵二叉树，求这棵二叉树上左右两个树枝上数量不小于n的所有结点

解题步骤：

建图
深度优先搜索

代码：

## 1. 初始化
m,n = map(int,input().split(" ")) 
#input()取到第一行输入,int把str转换成int；
#map用于多参数多返回值的函数计算，
#例如：res1,res2 = map(func(),输入参数)#树中所有成员的初始字典——key为输入值, value为对应的树结点对象，提前告诉编译器‘*’值的结点对象为None,否则*.val=*
mem = {"*":None} #这里使用字典是为了把每个输入与结点对象对应
degree = set()#除了根节点以外的所有结点的集合
# 目的：最后用mem-degree就可以知道谁是根节点，用集合存储可以自动去重## 2.构建二叉树图：把所有输入变成结点对象，并让每个结点知道自己的左右孩子
#2.1 定义结点类
class ListNode:def __init__(self,x):#初始一个结点对象的值是它自身，左右结点都为空self.val = xself.left = Noneself.right = None#2.2 把字符输入变成结点对象
# 循环m次（有m个推荐表，_为占位符）
for _ in range(m):root,left,right = input().split() #每人推荐的两个人分别为左右孩子（这里仅为定义变量名，还未起到实质作用）#把字符输入变成结点对象if root not in mem: mem[root] = ListNode(root)if left not in mem:mem[left] = ListNode(left)if right not in mem:mem[right] = ListNode(right)#  把新的成员结点加入到集合中（自动去重）degree.add(left)degree.add(right)# 2.3 把父节点和子节点真正地串联起来_root,_left,_right = mem[root],mem[left],mem[right]_root.left = _left_root.right = _right
#注：树的结构是保存在每个结点的结点对象里的，即让每个结点找到他们的左右结点# 2.4 找到树的根节点
#root 节点是入度为0的节点  
root = (set(mem) - degree).pop() #用pop()取得集合中的元素，否则取到的是有一个对象的集合# 3. 查找——DFS
#建立用来存储结果的全局变量
global ans
ans = []#DFS查找函数，查找到符合条件的结果放入全局变量ans中
#DFS，常规操作
def dfs(root):global ans # 记住全局变量也需要在函数中再声明一遍，不然访问不到if root: # 如果结点不为空，找他们的左右孩子left = dfs(root.left) #得到左边分支上结点个数right = dfs(root.right) #得到右边分支上结点的个数this = left + right + 1  #这个位置结点的数量需要加上它自身（1），否则对于它的上一层结点来说，就会少掉1个结点的数量if this >= n + 1:  # 因为这里算推荐新客户的数量不小于n，需要减掉推荐人自身，即this-1>=nans.append(root.val) #推荐新客户数量不少于2时加入到结果列表中return this # 返回当前结点的左右分支结点数再加上它自己一个，给他的父节点return 0 # 如果结点为空，返回该位置结点的数量为0#调用查找函数计算结果，传入之前建图后找到的根节点开始
dfs(mem[root])
if ans: #如果结果不为空print(" ".join(ans)) #按格式输出
else: # 否则
#None也要print出来，不然会少一个回车符print(None)