VIJOS-P1026 毒药？解药？

Description

羽毛笔和im是抽签到同一个考场的，她们突然闻到一阵刺鼻的化学试剂的气味。
机灵鼠：（头都不抬）你们是考生么？还在门口磨蹭什么？快进来帮我忙！！……怎么还不进来？你们拖赛，拖赛，把你们的青春都拖掉赛……
im：开…开策了> _<
羽毛笔：哎呀~~机灵鼠大人要我们帮什么忙？^^
机灵鼠：你们看这里的这些药，都是我研制的对付各种症状的解药。可是我一个不小心，每种药都小小地配错了一点原料，所以这些药都有可能在治愈某些病症的同时又使人患上某些别的病症……（im：那…那是解药还是毒药啊？！）……经过我天才的努力（背景：我是天才！！），终于弄清了每种药的具体性能（路人甲：那是你自己配的吗？-_-），我会把每种药能治的病症和能使人患上的病症列一张清单给你们，然后你们要根据这张清单找出能治愈所有病症的最少药剂组合……顺便说一声，病症的数目不超过10种（小呆：偶是好人吧^^），我的药是用不完的，就是说每种药剂都可以被重复使用。给你们的单子里第一行是病症的总数n，第二行是药剂的种类m（0< m< =100），以下有m行，每行有n个数字用空格隔开，文件的第i+2行的n个数字中，如果第j个数为1，就表示第i种药可以治愈病症j（如果患有这种病的话则治愈，没有这种病则无影响），如果为0表示无影响，如果为-1表示反而能使人得上这种病（无病患上，有病无影响）。我制的药任何两种性能都不同。你们只要给我用的最少的药剂数就可以了。给你们个样例：

Sample Input

3
2
1 0 1
-1 1 0

Sample Output

2

HINT

其实还有可能用尽了所有的药也不能将所有病治愈（真是不好意思嗬^^bb），那样的话你们只要写上“The patient will be dead.”就可以了。 im：做不出来啊哇啊啊啊（暴走中） 羽毛笔：哎呀~~im……来来吃药了。^^

Source

VIJOS

---

状态压缩BFS

Solution：

很显然我们首先会得到一个N*M的表格，表示第i种要对于第j种症状的作用效果。当N等于3的情况，可以得到如下的几种状态：

√	×
1	2 3
2	1 3
3	1 2
1 2	3
1 3	2
2 3	1
1 2 3	∅
∅	1 2 3

一共会有8中状态，同理 可以得到更普遍的结论：N种病共有$2^{N}$种状态；
这样我们就会有两种方法：
方法一：
若状态i可以转移成状态j，则i->j 可以建一条有向边。然后跑最短路就好。
但是说着简单，其实还是有很多注意事项的。先上代码：
Code：

#include <stdio.h>
#include <string.h>
#include <queue>
#define MAXN 1<<(10)+1
using namespace std;
int n,m,st,ed;
int a[150][15],dep[MAXN],visit[MAXN];
void spfa(int src)
{memset(dep,0x3f,sizeof(dep));dep[src]=0;queue<int>Q;Q.push(src);while(!Q.empty()){int u=Q.front();Q.pop();for(int i=1;i<=m;i++){int tmp=u;for(int j=1;j<=n;j++){   if((tmp&(1<<(j-1)))&&a[i][j]==1)    // 二进制情况下，第j位为 1 : - > 有病 //并且当前药物可以治疗 {tmp-=1<<(j-1);                  //让 第 j 位变成 0 }if((!(tmp&(1<<(j-1))))&&a[i][j]==-1){tmp+=1<<(j-1);}}if(dep[tmp]>dep[u]+1)   //当前情况达到 tmp 的步数 能 更新 {dep[tmp]=dep[u]+1;if(!visit[tmp]){visit[tmp]=1;Q.push(tmp);                    }}}}
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){scanf("%d",&a[i][j]);}}st=0,ed=(1<<n)-1;spfa(ed);if(dep[0]==0x3f3f3f3f){puts("The patient will be dead.") ; }else printf("%d\n",dep[0]);return 0;
}

解释与说明：
用二进制表示，假设一共有N种病，令111…1（N个1）表示所有病都患，0就是没有病，则st=0，ed=(1 < < N )-1就是N个1 的十进制表示。
然后BFS时只要判断st能不能转移到ed就可以。
PS：位运算大法Newbility
方法二：
Hash表判重，原理同上。

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct node
{int dep;int b[15];
}list[1<<10+1];
int n,m,st,ed;
int mp[150][15];
bool hash[1<<10+1];
void bfs()
{memset(hash,false,sizeof(hash));st=0,ed=(1<<n)-1;int head=1,tail=1;while(head<=tail){for(int i=1;i<=m;i++){tail++;st=0;for(int j=1;j<=n;j++){if(mp[i][j]==1) list[tail].b[j]=1;if(mp[i][j]==0) list[tail].b[j]=list[head].b[j];if(mp[i][j]==-1)list[tail].b[j]=0;if(list[tail].b[j]==1)  st+=(1<<(j-1));}if(!hash[st]){hash[st]=true;list[tail].dep=list[head].dep+1;if(st==ed){printf("%d\n",list[tail].dep);exit(0);}}else tail--;}head++;}
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){scanf("%d",&mp[i][j]);}}bfs();printf("The patient will be dead.\n");return 0;
}

---

POJ3321【Apple Tree】

Time Limit: 2000MS Memory Limit: 65536K
Total Submissions: 21614 Accepted: 6563

Description

There is an apple tree outside of kaka’s house. Every autumn, a lot of apples will grow in the tree. Kaka likes apple very much, so he has been carefully nurturing the big apple tree.

The tree has N forks which are connected by branches. Kaka numbers the forks by 1 to N and the root is always numbered by 1. Apples will grow on the forks and two apple won’t grow on the same fork. kaka wants to know how many apples are there in a sub-tree, for his study of the produce ability of the apple tree.

The trouble is that a new apple may grow on an empty fork some time and kaka may pick an apple from the tree for his dessert. Can you help kaka?

Input

The first line contains an integer N (N ≤ 100,000) , which is the number of the forks in the tree.
The following N - 1 lines each contain two integers u and v, which means fork u and fork v are connected by a branch.
The next line contains an integer M (M ≤ 100,000).
The following M lines each contain a message which is either
“C x” which means the existence of the apple on fork x has been changed. i.e. if there is an apple on the fork, then Kaka pick it; otherwise a new apple has grown on the empty fork.
or
“Q x” which means an inquiry for the number of apples in the sub-tree above the fork x, including the apple (if exists) on the fork x
Note the tree is full of apples at the beginning

Output

For every inquiry, output the correspond answer per line.

Sample Input

3
1 2
1 3
3
Q 1
C 2
Q 1

Sample Output

3
2

Source

POJ Monthly–2007.08.05, Huang, Jinsong

---

DFS序【树状数组维护】

Solution：

以下图为例：

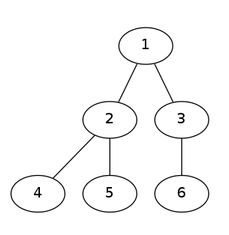
DFS序：

对图进行深度优先遍历时,按访问顶点的先后次序得到的顶点序列称为该图的深度优先遍历序列,或简称为DFS序列

所以对于上图来说，它的DFS序可以是 1 3 6 2 4 5也可以是1 2 4 5 3 6
对于一个点来说，它会有两个时间戳，一个进栈的时间戳一个出栈的时间戳，用in[i],out[i]表示

i	in[i]	out[i]
1	1	6
2	4	6
3	2	3
4	6	6
5	5	5
6	3	3

然后我们就可以发现，在DFS序中in[i]~out[i]的数字就是i的子树编号。
所以我们就需要处理出来in[],out[]数组然后用树状数组维护增减以及求和就好了。
Code：

#include <stdio.h>
#include <string.h>
#define MAXN 150000
struct node
{int from;int to;int next;
}edge[MAXN];
int n,m,cnt,tot,tmp;
int head[MAXN],c[MAXN],order[MAXN],in[MAXN],out[MAXN];
bool judge[MAXN];
void init()
{memset(head,-1,sizeof(head));cnt=1;
}
void addedge(int from,int to)
{edge[cnt].from=from;edge[cnt].to=to;edge[cnt].next=head[from];head[from]=cnt++;
}
int lowbit(int x)
{return x&(-x);
}
int get_sum(int x)
{int sum=0;while(x){sum+=c[x];x-=lowbit(x);}return sum;
} 
void update(int x,int val)
{while(x<=MAXN){c[x]+=val;x+=lowbit(x);}
}
void dfs(int u)
{in[u]=++tot;    //进入 时间戳 order[tot]=u;for(int i=head[u];i!=-1;i=edge[i].next){int v=edge[i].to;dfs(v);}out[u]=tot;     //退出 时间戳 
}
int main()
{init();scanf("%d",&n);for(int i=1;i<=n-1;i++){int a,b;scanf("%d%d",&a,&b);addedge(a,b);}dfs(1);for(int i=1;i<=n;i++){update(i,1);judge[i]=true;}/*for(int i=1;i<=tot;i++){printf("%d:",i);for(int j=in[i];j<=out[i];j++){printf("%d ",order[j]);}printf("\n");}*/ scanf("%d",&m);char s[3];for(int i=1;i<=m;i++){scanf("%s %d",s,&tmp);if(s[0]=='Q'){printf("%d\n",get_sum(out[tmp])-get_sum(in[tmp]-1));}else {if(judge[tmp]==false){update(in[tmp],1);judge[tmp]=true;}else{update(in[tmp],-1);judge[tmp]=false;   }}}return 0;
}

---

POJ3764【The xor-longest Path】

Description

In an edge-weighted tree, the xor-length of a path p is defined as the xor sum of the weights of edges on p:

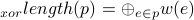
⊕ is the xor operator.

We say a path the xor-longest path if it has the largest xor-length. Given an edge-weighted tree with n nodes, can you find the xor-longest path? 　

Input

The input contains several test cases. The first line of each test case contains an integer n(1<=n<=100000), The following n-1 lines each contains three integers u(0 <= u < n),v(0 <= v < n),w(0 <= w < 2^31), which means there is an edge between node u and v of length w.

Output

For each test case output the xor-length of the xor-longest path.

Sample Input

4
0 1 3
1 2 4
1 3 6

Sample Output

7

Hint

The xor-longest path is 0->1->2, which has length 7 (=3 ⊕ 4)

---

Solution：

异或的性质：a^b=(a^c)^(b^c);
所以可以把根节点当做c,即 i - > j 路径上的Xor
$F(i,j)=F(1,i)$^$F(1,j)$
而$F(i,j)$可以通过搜索处理出来。 但是O（N^2）的枚举肯定会超时，所以可以用01字典树来把一个数用二进制的形式储存起来，这样就会得到一个深度最大为32的01树。
Time complexity：O( n*log2( Max(Xor[i,z]) ) )=**O(n*30),**0<=i < n

然后用类似贪心的思想从最高按位查找直到最低位，每一位查找时，如果树中有其当前互异的值存在，则累加该位的权值，并按此方向往下一位查找；否则不累加权值，并按Xor[i,z]的该位上的数字进入下一层。最终累加得到的值即为所求最大值。

#include <stdio.h>
#include <string.h>
#define MAXN 100100
typedef long long ll;
struct node
{ll from;ll to;ll next;ll val;
}edge[MAXN<<1];
ll n,cnt,v,size=1,ans=-1;
ll head[MAXN],dis[MAXN],next[3000000][2];
ll max( ll a , ll b ){ return a > b ? a : b ; }
void init()
{memset(head,-1,sizeof(head));memset(next,0,sizeof(next));memset(dis,0,sizeof(dis));ans=-1,size=cnt=1;
}
void addedge(ll from,ll to,ll val)
{edge[cnt].from=from;edge[cnt].to=to;edge[cnt].val=val;edge[cnt].next=head[from];head[from]=cnt++;
}
void dfs(ll x,ll fa,ll d)
{dis[x]=d;for(ll i=head[x];i!=-1;i=edge[i].next){if((v=edge[i].to)!=fa){dfs(v,x,d^edge[i].val);}}
}
ll newnode()
{memset(next[size],0,sizeof(next[size]));return size++;
}
void Insert(ll x)
{ll p=0;bool index;for(ll i=31;i>=0;i--)   //从高位开始 贪心{index=x&(1ll<<i)?1:0;   //获得x二进制上第 i+1 位的数字 if(!next[p][index])     //如果未开空间 {next[p][index]=newnode();}p=next[p][index];       // 指针后移 进入下一层 } 
}
void find(ll x)
{ll p=0,w=0;bool index;for(ll i=31;i>=0;i--){index=x&(1ll<<i)?0:1;//获得x二进制上第i+1位数字的 非if(next[p][index]){w|=1ll<<i;      //加上该位的权值 p=next[p][index];     } else p=next[p][!index];}ans=max(ans,w);
}
int main()
{while(~scanf("%lld",&n)){init();for(ll i=1;i<=n-1;i++){ll a,b,c;scanf("%lld%lld%lld",&a,&b,&c);a++,b++;addedge(a,b,c);addedge(b,a,c);}dfs(1,0,0);for(ll i=1;i<=n;i++){Insert(dis[i]);find(dis[i]);}printf("%lld\n",ans);}return 0;
} 
/*
4
0 1 3
1 2 4
1 3 6
*/