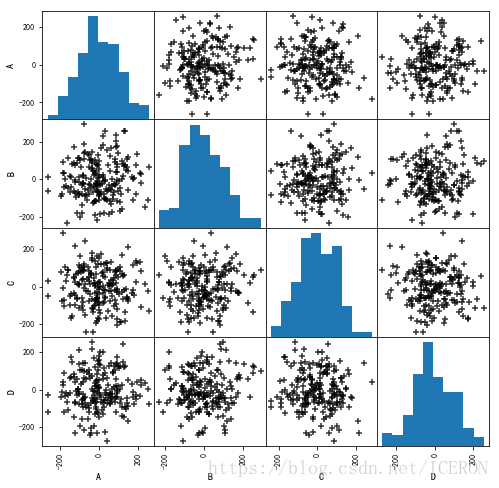
相关性分析
作者:学者科技
时间:2022/12/25
应用场景
- 发现数据之间的关联性
- 比如 啤酒 和 尿布
- 删减统计指标
- 比如 城市里的温度传感器,相关性强的可以去掉以节约成本
- 挑选回归建模的变量
- 选择与因变量相关性高的自变量
- 自变量间如果有高度地相关性,也需要删减
- 验证主观判断
决策层或者管理层经常会根据自己的经验,主观地形成一些逻辑关系。最典型的表述方式就是“我认为这个数据会影响到那个数据”。到底有没有影响?可以通过计算相关系数来判断。相关系数的应用能够让决策者更冷静,更少地盲目拍脑袋。虽然相关系数
不能表达因果关系,但有联系的两件事情,一定会在相关系数上有所反映
协方差
推导
设X,Y是两个随机变量,则有
D ( X + Y ) = E ( ( ( X + Y ) − E ( X + Y ) ) 2 ) = E ( ( ( X + Y ) − E ( X ) − E ( Y ) ) 2 ) = E ( ( ( X − E ( X ) ) + ( Y − E ( Y ) ) ) 2 ) = E ( ( X − E ( X ) ) 2 ) + E ( ( Y − E ( Y ) ) 2 ) + 2 E ( ( X − E ( X ) ) ( Y − E ( Y ) ) ) = D ( X ) + D ( Y ) + 2 E [ ( X − E ( X ) ) ( Y − E ( Y ) ) ] \begin{align} D(X + Y) &= E(((X+Y) - E(X + Y))^2) \\ &= E(((X+Y) - E(X) - E(Y))^2) \\ &= E(((X - E(X)) + (Y - E(Y)))^2) \\ &= E((X - E(X))^2) + E((Y - E(Y))^2) \\ &\ \ + 2E((X-E(X))(Y - E(Y))) \\ &= D(X)+D(Y) + 2E [ (X - E(X))(Y- E(Y)) ] \end{align} D(X+Y)=E(((X+Y)−E(X+Y))2)=E(((X+Y)−E(X)−E(Y))2)=E(((X−E(X))+(Y−E(Y)))2)=E((X−E(X))2)+E((Y−E(Y))2) +2E((X−E(X))(Y−E(Y)))=D(X)+D(Y)+2E[(X−E(X))(Y−E(Y))]
当 X X X, Y Y Y相互独立时, X − E ( X ) X - E(X) X−E(X) 与 Y − E ( Y ) Y - E(Y) Y−E(Y) 也相互独立,因此
E ( ( X − E ( X ) ( Y − E ( Y ) ) = E ( X − E ( X ) ) ∗ E ( Y − E ( Y ) ) = ( E ( X ) − E ( X ) ) ∗ ( E ( Y ) − E ( Y ) ) = 0 \begin{align} E((X - E(X)(Y - E(Y)) &= E(X - E(X)) * E(Y - E(Y)) \\ &= (E(X) - E(X)) * (E(Y) - E(Y)) \\ &= 0 \end{align} E((X−E(X)(Y−E(Y))=E(X−E(X))∗E(Y−E(Y))=(E(X)−E(X))∗(E(Y)−E(Y))=0
于是
X , Y 相互独立 ⟹ E ( ( X − E ( X ) ( Y − E ( Y ) ) = 0 X, Y相互独立 \implies E((X - E(X)(Y - E(Y)) = 0 X,Y相互独立⟹E((X−E(X)(Y−E(Y))=0
它的逆否命题同样成立:
E ( ( X − E ( X ) ( Y − E ( Y ) ) ≠ 0 ⟹ X , Y 不相互独立 E((X - E(X)(Y - E(Y)) \neq 0 \implies X, Y不相互独立 E((X−E(X)(Y−E(Y))=0⟹X,Y不相互独立
E((X - E(X)(Y - E(Y)) 从某种程度上刻划了两个随机变量的相关性,为了方便我们把它称为协方差。记作:
C o v ( X , Y ) = E ( ( X − E ( X ) ( Y − E ( Y ) ) \rm{Cov}(X,Y) = E((X - E(X)(Y - E(Y)) Cov(X,Y)=E((X−E(X)(Y−E(Y))
该式可继续推导成更加常用的公式:
C o v ( X , Y ) = E ( ( X − E ( X ) ( Y − E ( Y ) ) = E ( X Y − X E ( Y ) − E ( X ) Y + E ( X ) E ( Y ) ) = E ( X Y ) − E ( X ) E ( Y ) − E ( X ) E ( Y ) + E ( X ) E ( Y ) = E ( X Y ) − E ( X ) E ( Y ) \begin{align} \rm{Cov}(X,Y) &= E((X - E(X)(Y - E(Y)) \\ &= E(XY - XE(Y) -E(X)Y + E(X)E(Y)) \\ &= E(XY) - E(X)E(Y) - E(X)E(Y) + E(X)E(Y) \\ &= E(XY) - E(X)E(Y) \end{align} Cov(X,Y)=E((X−E(X)(Y−E(Y))=E(XY−XE(Y)−E(X)Y+E(X)E(Y))=E(XY)−E(X)E(Y)−E(X)E(Y)+E(X)E(Y)=E(XY)−E(X)E(Y)
根据协方差取值的不同,我们规定:
- 当
Cov(X,Y) > 0, X,Y正相关 - 当
Cov(X,Y) < 0, X,Y负相关 - 当
Cov(X,Y) = 0, X,Y不相关
例题
假设有如下X,Y的联合概率分布,计算 Cov(X,Y),并确定X,Y的相关性。
| X\Y | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 0.07 | 0.09 | 0.06 | 0.01 |
| 1 | 0.07 | 0.06 | 0.07 | 0.01 |
| 2 | 0.06 | 0.07 | 0.14 | 0.03 |
| 3 | 0.02 | 0.04 | 0.16 | 0.04 |
解:首选计算X*Y的所有可能取值
| XY | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 |
| 2 | 0 | 2 | 4 | 6 |
| 3 | 0 | 3 | 6 | 9 |
容易得到X,Y各自的边缘分布如下
| X | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| P | 0.23 | 0.21 | 0.30 | 0.26 |
| Y | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| P | 0.22 | 0.26 | 0.43 | 0.09 |
然后计算期望, 最后套用协方差公式:
E(XY) = 0 * 0.07 + 0 * 0.09 + ... +0 * 0.07 + 1 * 0.06 + ... +0 * 0.06 + 2 * 0.07 + ... +...= 2.55
E(X) = 1.59
E(Y) = 1.39
Cov(X, Y) = E(XY) - E(X)E(Y) = 0.34
Cov(X, Y) > 0 , 因此X,Y正相关
相关系数
定义
协方差是有量纲的。例如X表示身高(单位是m),Y表示体重(单位是kg)。则Cov(X,Y)带有量纲 ( m ⋅ k g ) (m\cdot kg) (m⋅kg)。
为了消除量纲,定义如下新的概念:
C o r r ( X , Y ) = C o v ( X , Y ) σ X σ Y , s . t . σ X , σ Y > 0 \rm{Corr}(X,Y) = \frac{\rm{Cov}(X,Y)}{\sigma_X \sigma_Y} \ \ \ , s.t. \ \sigma_X, \sigma_Y \gt 0 Corr(X,Y)=σXσYCov(X,Y) ,s.t. σX,σY>0
这个概念被称为相关系数。可以看出,相关系数的符号与协方差相同,这说明相关系数的取值也可返映X与Y的相关性:
- 当
Corr(X,Y) > 0, X,Y正相关 - 当
Corr(X,Y) < 0, X,Y负相关 - 当
Corr(X,Y) = 0, X,Y不相关
相关系数是有取值范围的,由 施瓦茨(Schwarz)不等式导出。不等式推导如下:
首先考虑如下二次函数:
g ( t ) = E 2 ( t ( X − E ( X ) ) + Y − E ( Y ) ) = t 2 σ X 2 + σ Y 2 + 2 t ⋅ C o v ( X , Y ) > 0 \begin{align} g(t) &= E^2(t(X-E(X)) + Y - E(Y)) \\ &= t^2 \sigma^2_X + \sigma^2_Y + 2t\cdot \rm{Cov}(X, Y) \\ &> 0 \end{align} g(t)=E2(t(X−E(X))+Y−E(Y))=t2σX2+σY2+2t⋅Cov(X,Y)>0
即 方程 g ( t ) = 0 g(t) = 0 g(t)=0 无解, 所以由 $\Delta = 4 \rm{Cov}^2(X, Y) - 4 \sigma^2_X \sigma^2_Y \le 0 $ 得到如下Schwarz不等式:
C o v 2 ( X , Y ) ≤ σ X 2 σ Y 2 \rm {Cov}^2(X,Y) \le \sigma_X^2 \sigma_Y^2 Cov2(X,Y)≤σX2σY2
所以得相关系数的取值范围为 -1~1。
C o r r 2 ( X , Y ) = C o v 2 ( X , Y ) σ X 2 σ Y 2 ≤ 1 \rm{Corr^2(X, Y)} = \frac{\rm {Cov}^2(X,Y) }{\sigma_X^2 \sigma_Y^2} \le 1 Corr2(X,Y)=σX2σY2Cov2(X,Y)≤1
其它结论:
- 当
Corr(X, Y) = 1 或 -1时,X与Y呈线性相关。证明过程略。 - 当
Corr(X, Y) = 0时,X与Y不相关。 不相关是指X与Y没有线性关系,但可能有其它函数关系,譬如平方关系,对数关系等。 - 当
Corr(X, Y) = 其它时,X与Y有一定程度的线性关系
例题
已知随机向量 ( X , Y ) (X, Y) (X,Y)的联合密度函数为 p ( x , y ) p(x,y) p(x,y),求相关系数 C o r r ( X , Y ) \rm{Corr}(X,Y) Corr(X,Y)。
解:
p X ( x ) = ∫ − ∞ ∞ p ( x , y ) d y p Y ( y ) = ∫ − ∞ ∞ p ( x , y ) d x E ( X ) = ∫ − ∞ ∞ p X ( x ) ⋅ x d x E ( Y ) = ∫ − ∞ ∞ p Y ( y ) ⋅ y d y E ( X 2 ) = ∫ − ∞ ∞ p X ( x ) ⋅ x 2 d x E ( Y 2 ) = ∫ − ∞ ∞ p Y ( y ) ⋅ y 2 d y E ( X Y ) = ∫ − ∞ ∞ ∫ − ∞ ∞ p ( x , y ) ⋅ x ⋅ y d x d y D ( X ) = E ( X 2 ) − E 2 ( X ) D ( Y ) = E ( Y 2 ) − E 2 ( Y ) C o r r ( X , Y ) = C o v ( X , Y ) ( D ( X ) ) ( D ( Y ) ) = E ( X Y ) − E ( X ) E ( Y ) ( D ( X ) ) ( D ( Y ) ) p_X(x) = \int_{-\infty}^{\infty} p(x, y) dy \\ p_Y(y) = \int_{-\infty}^{\infty} p(x, y) dx \\ E(X) = \int_{-\infty}^{\infty} p_X(x) \cdot x \ dx \\ E(Y) = \int_{-\infty}^{\infty} p_Y(y) \cdot y \ dy \\ E(X^2) = \int_{-\infty}^{\infty} p_X(x) \cdot x^2 \ dx \\ E(Y^2) = \int_{-\infty}^{\infty} p_Y(y) \cdot y^2 \ dy \\ E(XY) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} p(x, y) \cdot x \cdot y \ dxdy \\ D(X) = E(X^2) - E^2(X) \\ D(Y) = E(Y^2) - E^2(Y) \\ \rm{Corr}(X, Y) = \frac{\rm{Cov}(X, Y)}{ \sqrt(D(X)) \sqrt(D(Y)) } = \frac{E(XY) - E(X)E(Y)}{ \sqrt(D(X)) \sqrt(D(Y)) } pX(x)=∫−∞∞p(x,y)dypY(y)=∫−∞∞p(x,y)dxE(X)=∫−∞∞pX(x)⋅x dxE(Y)=∫−∞∞pY(y)⋅y dyE(X2)=∫−∞∞pX(x)⋅x2 dxE(Y2)=∫−∞∞pY(y)⋅y2 dyE(XY)=∫−∞∞∫−∞∞p(x,y)⋅x⋅y dxdyD(X)=E(X2)−E2(X)D(Y)=E(Y2)−E2(Y)Corr(X,Y)=(D(X))(D(Y))Cov(X,Y)=(D(X))(D(Y))E(XY)−E(X)E(Y)
Spearman 秩相关系数(等级相关系数)
假设有 X X X, Y Y Y两个随机变量并采集了N对样本 ( X i , Y i ) , i ∈ 1.. N (X_i, Y_i), i \in 1..N (Xi,Yi),i∈1..N。
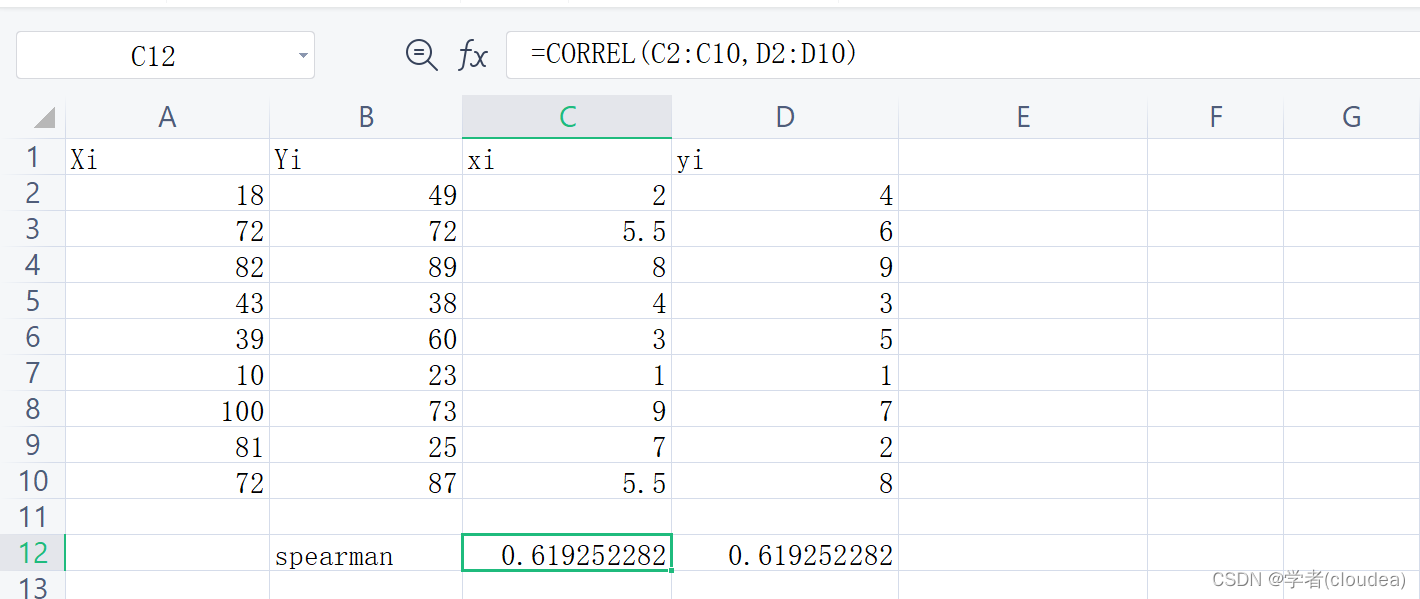
用 x i x_i xi表示 X i X_i Xi 在X样本中的次序, 用 y i y_i yi表示 Y i Y_i Yi 在Y样本中的次序。则Spearman 相关系数定义为:
ρ = ∑ i = 1 N ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 N ( x i − x ˉ ) 2 ∑ i = 1 N ( y i − y ˉ ) 2 = C o r r ( x , y ) \rho=\frac{\sum_{i=1}^{N}(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum_{i=1}^{N}(x_i-\bar{x})^2 \sum_{i=1}^{N}(y_i-\bar{y})^2}}= \rm{Corr}(x,y) ρ=∑i=1N(xi−xˉ)2∑i=1N(yi−yˉ)2∑i=1N(xi−xˉ)(yi−yˉ)=Corr(x,y)
举个例子:


Kendall 秩相关系数(等级相关系数)
假设有 X X X, Y Y Y两个随机变量并采集了n对样本 ( X i , Y i ) , i ∈ 1.. n (X_i, Y_i), i \in 1..n (Xi,Yi),i∈1..n。
Kendall有三种定义分别为 τ a , τ b , τ c \tau_a,\tau_b,\tau_c τa,τb,τc。 前者只适用于X,Y都没有重复值的情况。当X,Y都没有重复值时,前者将与后两者值相同。
τ a = ( P − Q ) n ( n − 1 ) / 2 τ b = P − Q ( P + Q + T ) ⋅ ( P + Q + U ) τ c = ( P − Q ) n 2 ( m − 1 ) / 2 m \begin{align} \tau_a&= \frac{ (P- Q)}{n(n-1)/2} \\ \tau_b&=\frac{P - Q}{\sqrt{(P+Q+T)\cdot (P+Q+U)}} \\ \tau_c&=\frac{(P-Q)}{n^2(m - 1)/2m} \end{align} τaτbτc=n(n−1)/2(P−Q)=(P+Q+T)⋅(P+Q+U)P−Q=n2(m−1)/2m(P−Q)
- 当 τ = 1 \tau = 1 τ=1 时,X,Y具有相关性
- 当 τ = − 1 \tau = -1 τ=−1 时,X,Y具有相反的相关性
- 当 τ = 0 \tau = 0 τ=0 时,X,Y相互独立
其中,P表示一致的数量,Q不一致的数量,T表示在仅X中的ties个数,U表示仅在Y中的ties个数。n是样本数量。m是X或Y中独特值的个数中的较小值。如下图:
- 一致: x i < x j x_i < x_j xi<xj且 y i < y j y_i < y_j yi<yj 或 x i > x j x_i > x_j xi>xj且 y i > y j y_i > y_j yi>yj
- 不一致: x i < x j x_i < x_j xi<xj且 y i > y j y_i > y_j yi>yj 或 x i > x j x_i > x_j xi>xj且 y i < y j y_i < y_j yi<yj
- 仅在X中的ties: x i = x j x_i = x_j xi=xj且 y i ≠ y j y_i \neq y_j yi=yj
- 仅在Y中的ties: x i ≠ x j x_i \neq x_j xi=xj且 y i = y j y_i = y_j yi=yj
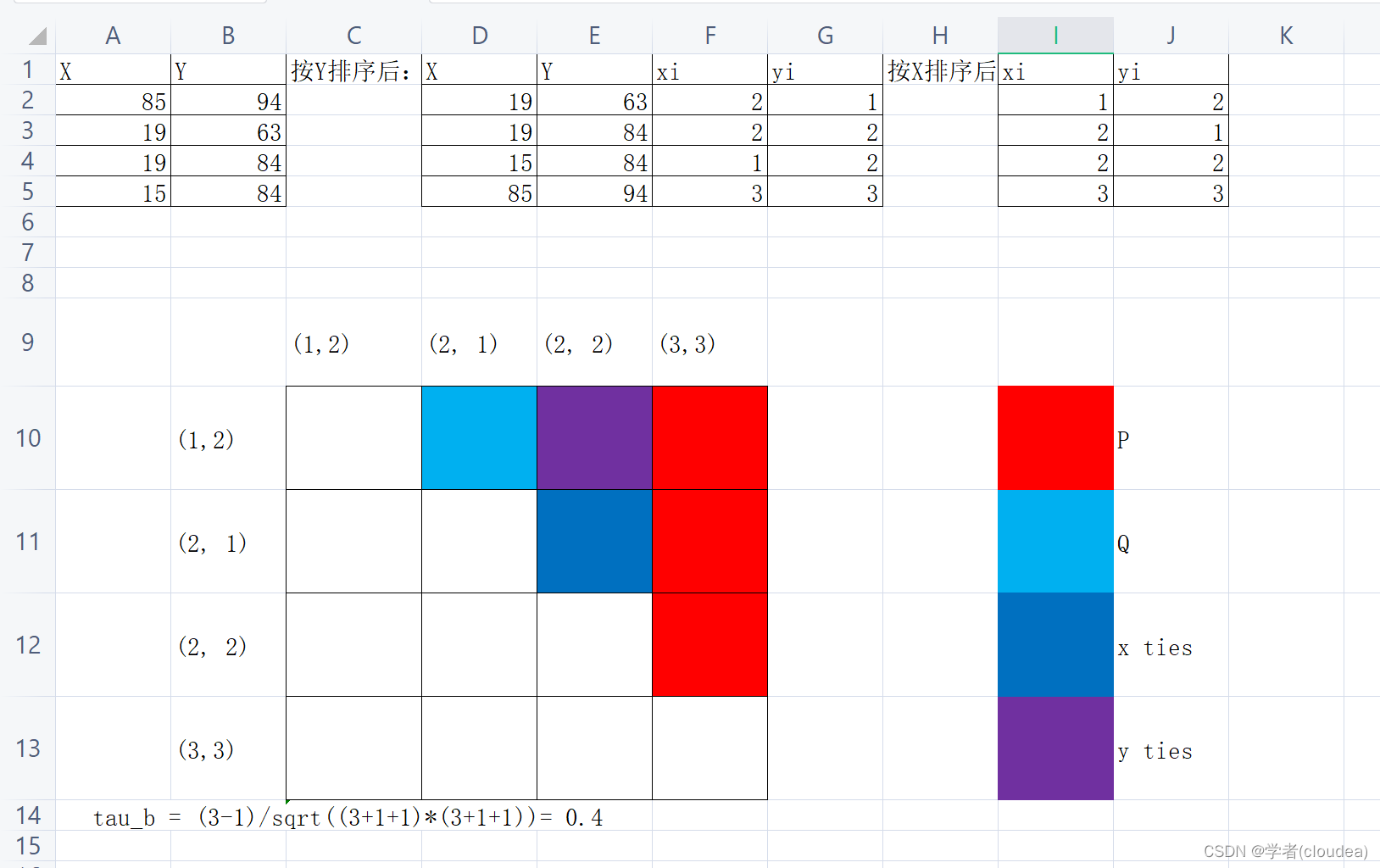
举个例子:
X = [85,19,19,15]
Y = [94,63,84,84]
# 先按照Y的顺序对X和Y调序,因为是同时调的,所有没啥影响
perm = argsort(Y) # [1,2,3,0]
X, Y = X[perm], Y[perm] # [19, 19, 15, 85], [63, 84, 84, 94]
y = dense(Y) # [1, 2, 2, 3]
# 按照X的顺序排序。同理,除了顺序没啥影响
perm = argsort(X) # [2, 0, 1, 3]
X, y = X[perm], y[perm] # [15, 19, 19, 85], [2, 1, 2, 3]
x = dense(X) # [1, 2, 2, 3]# 上述过程本质上是为X,Y中的元素确定一个序号。
# 如果是人工计算序号,可省略排序过程。# 有了x, y,如上图 可以计算P、Q、T、U等了
P=3
Q=1
T=1
U=1
n=4
m=3 # X中独特值个数是3,Y中独特值个数是3,取两者最小值,因此m=3
tau_b = (P - Q) / sqrt((P+Q+T)*(P+Q+U)) = 0.4
tau_c = (P - Q) / n*n*(m-1) / (2*m) = 0.375
Pearson系数:叫皮尔逊相关系数,也叫线性相关系数,用于进行线性相关分析,是最常用的相关系数,当数据满足正态分布时会使用该系数。
比如:身高和体重的相关性
Spearman系数:当数据不满足正态分布时,使用该系数。
比如:身高和“病情程度(初期、中期、晚期)”的相关性
Kendall系数:同Spearman系数
工具
- pandas
- numpy
- scipy
import numpy as np
import pandas as pd
import scipy.stats as statsif __name__ == "__main__":x = np.array([1, 2, 3, 4, 5, 6, 7])y = np.array([1, 4, 8, 24, 16, 30, 50])df = pd.DataFrame({"x": x, "y": y})print(np.corrcoef([x, y]))print(df.corr(method='pearson'))print(df.corr(method='spearman'))print(df.corr(method='kendall'))#df.corrWith(Series|DataFrame)print(stats.pearsonr(x, y)[0])print(stats.spearmanr(x, y)[0])print(stats.kendalltau(x, y)[0])

参考
[1] 概率论与数理统计教程(第二版)
[2] https://zhuanlan.zhihu.com/p/136771737
[3] https://zhuanlan.zhihu.com/p/367920869
[4] https://baike.baidu.com/item/%E7%A7%A9%E7%9B%B8%E5%85%B3%E7%B3%BB%E6%95%B0/3316537?fromModule=lemma_inlink
[5] 统计知识扫盲:相关系数
[6] Kendall tau distance理解与分析