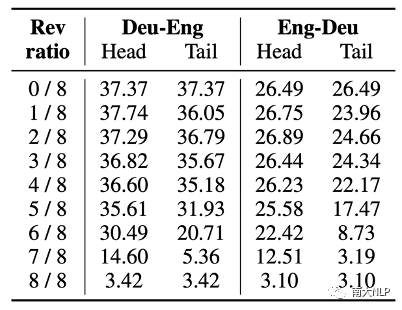
1. 隐私计算全貌



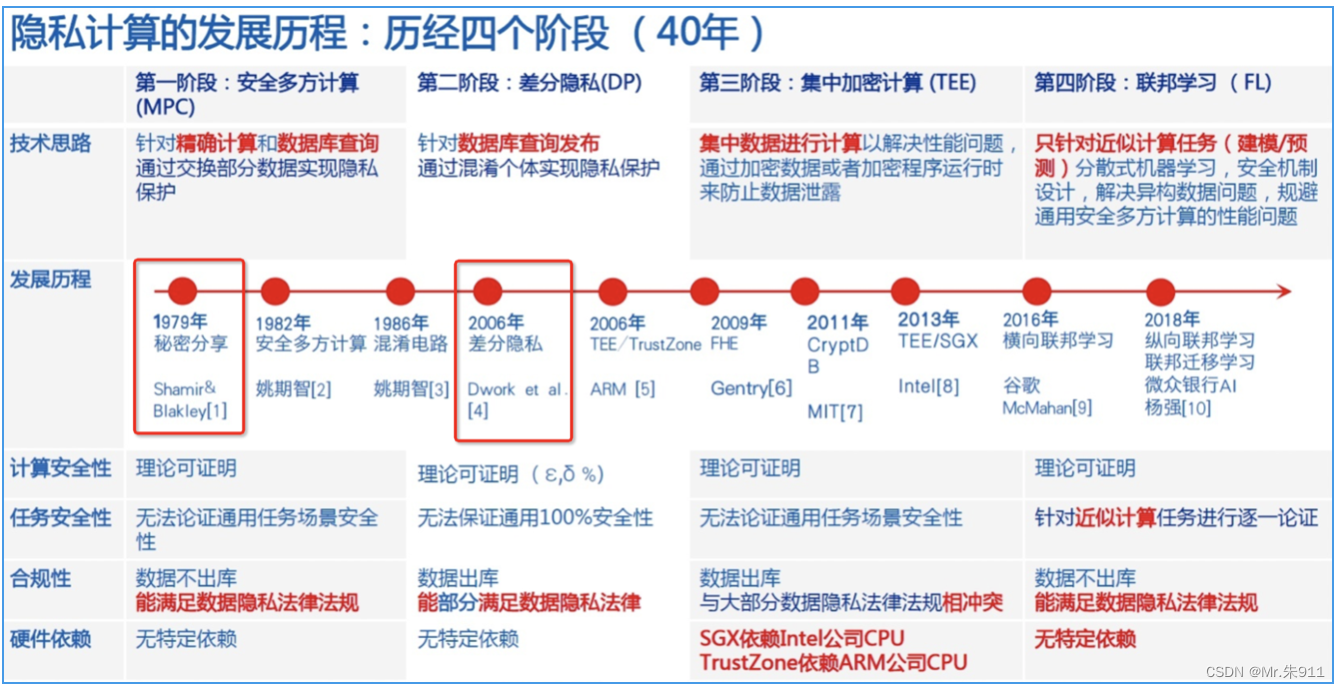
可以看到，隐私计算技术从1979年就开始了，历经四代从安全多方计算(MPC)、到差分隐私(DP)、到集中加密技术(TEE)，再到联邦学习(FL)。

2. 秘密共享

secret Sharing 就是“秘密分享”或者“秘密共享”，可以理解为：
现在有一个秘密(如一个整数 D)，不希望泄露出去。同时有 N 个人，如果每个人都知道这个秘密D，那么D就不安全了。但是如果把D进行切分随机的分给N个人，要用到的时候需要N个人的部分信息聚合到一起，才能解密D的值，那么是安全的。但是这种方案比较脆弱，如果一个人不在了，这个秘密就真成了无法探知的秘密了。
所以为了健壮性，设计了一种新的模式，在这种模式下，不需要所有的人一起解密，只需要一定的人数K（1 < K < N）就可以解密，这就是Shamir在1979 年发表在 ACM-Communication 的一个解法。

主要特性：

所以，可以将秘密分享分为两类：
严格的秘密分享：需要所有人一起解密；
阈值的秘密分享：不需要所有人，只需要满足一定人数，就可以解密；

2.1 阈值秘密分享

2.1.1 基本思路

阈值秘密分享的基本思路是，基于秘密分享的便携性与安全性的考量，如果有个n个秘密分片，我们只需要凑齐 k（ 1 < K <n ）个人，他们手中的信息拼凑起来，就可以获取秘密

那么如何才能做到这点呢？有以下几个问题需要考虑:

随机性：挑选的k个人，需要是随机挑选的k个人，不能是一个固定的选取。
必然性：随机选出的这k个人，必须能够将需要的数字进行解密。

那么，是什么样的技术可以实现呢？

大家还记得学习《线性代数》的时候吧，在线性代数的课上，k个参与者，相当于k个变量，那么需要k个方程就才可以解出来。

2.2.2 计算逻辑

加密逻辑：

秘密数字：S = 1234；
参与方：n = 6 个参与者，S1, S2, …，S6
域值：k = 3

1、首先构造出n个方程式，构造公式，这个公式是从文章How to Share a Secret里面分析的，说白了就是多项式，

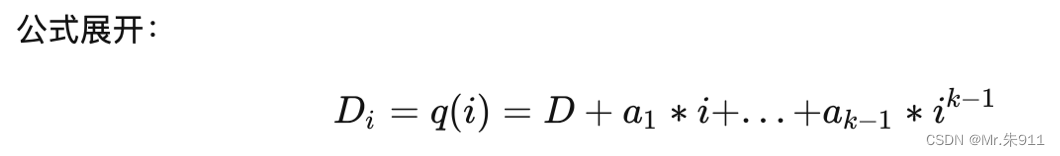
2、进行计算

解密逻辑：

参考文档：

https://en.wikipedia.org/wiki/Shamir%27s_Secret_Sharing

https://arxiv.org/pdf/2009.13153.pdf

https://dl.acm.org/doi/pdf/10.1145/359168.359176

3. 差分隐私

3.1 直观原理

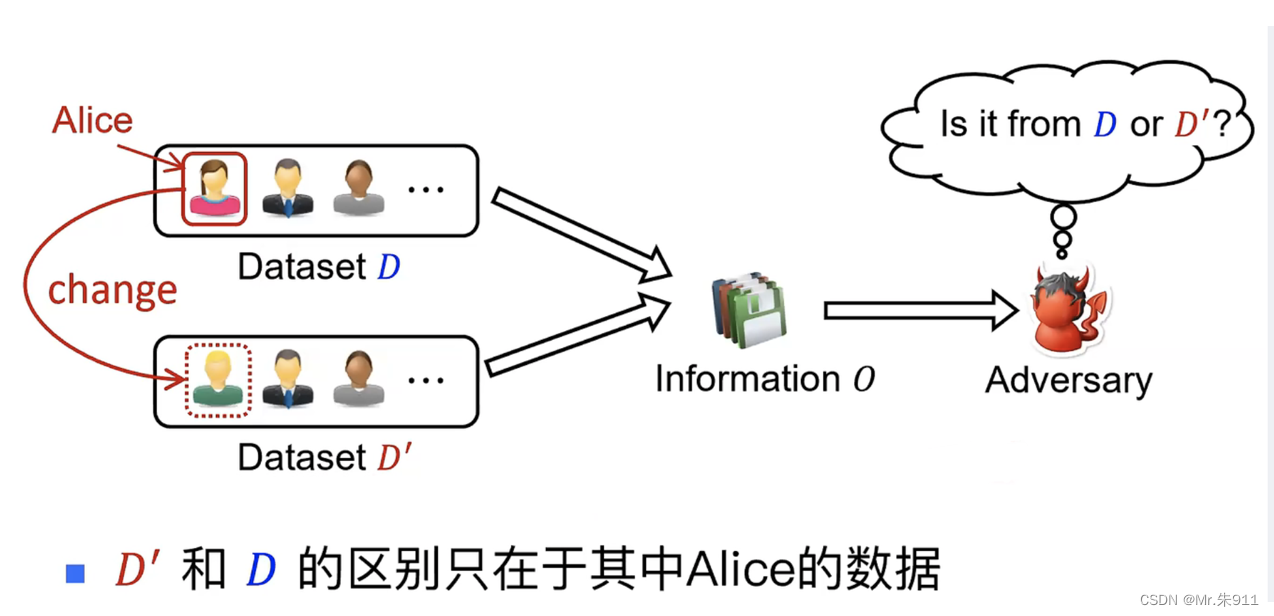
如果攻击者无法判别信息O是来自于D还是D’，那可以认为Alice的隐私受到了保护。

差分隐私要求任何被发布的信息应当避免让攻击者分辨出任何具体的个人数据。为此，差分隐私要求被发布的信息需经一个随机算法所处理，且该随机算法会对信息做一些扰动

3.2 定义

随机算法A满足ε -差分隐私，当且仅当以下式子

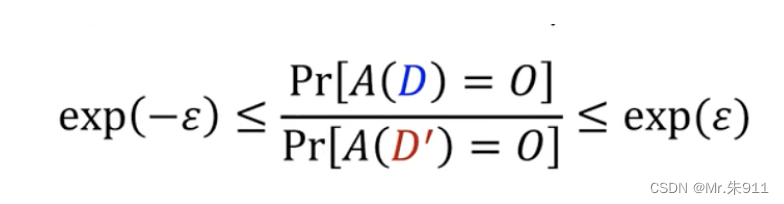
对任意“相邻”数据集D和D’及任意输出O都成立，差分隐私图示如下：

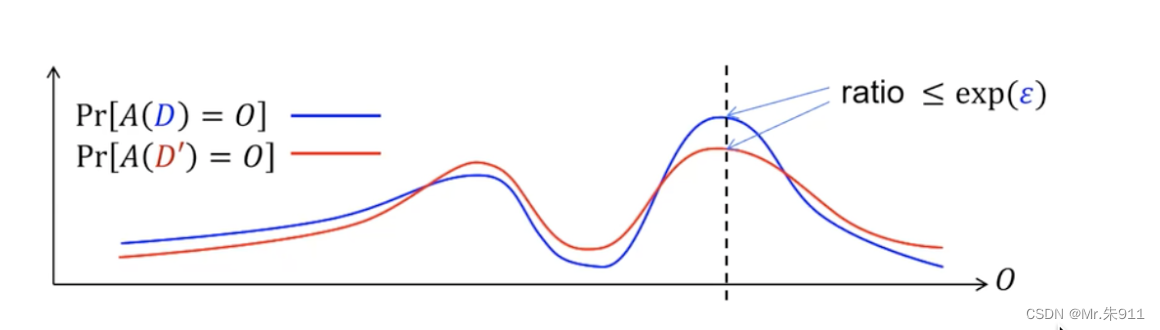
曲线差距越小，说明安全性越好，隐私保护越强
上面的定义意味着：修改一个人的数据，不会对算法A输出的分布带来太大的影响，也就是说当一个攻击者观察算法A的输出的时候，很难分辨出源数据到底是D还是D’

3.3 差分隐私算法

拉普拉斯机制和随机化回答是两个经典的差分隐私算法，当然还有许多其他不同的算法。
一般而言，不同的应用场景、不同的数据集、不同的输出往往需要不同的算法设计。

3.3.1 拉普拉斯机制

当发布数值型数据的时候，可以用拉普拉斯机制来引入噪声来满足差分隐私。

案例：假设我们有一个病患数据集 D，考虑以下数据库查询，如果我们要发布这个查询结果，如何才能满足ε -差分隐私。

1、首先，我们应该考虑这个查询的结果有多依赖于某个特定病人的信息？
如果我们修改数据集D中任意一个病患的数据，上述查询结果最多会改变1。这里的1代表了查询结果对于个体数据的依赖程度。

如果我们能用噪声掩盖这个最多为1的改变的话，我们就能满足差分隐私。

2、其次，我们可以往查询结果中加入一个服从拉普拉斯分布的噪声。

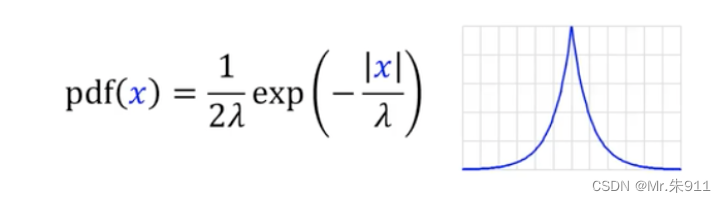
1. 该函数中值当x=0时，pdf(x) = 1/ 2λ为最大，两边成指数型下降；
2. 当参数设为 λ=1/ε ，即能满足ε-差分隐私（根据上面假设应为分子为1是因为上面假设的查询结果最多会改变1（敏感度为1））

一般而言，如果我们要发布一组数值型查询结果，通常会对每个结果加入独立的拉普拉斯噪声来满足差分隐私。并且噪声参数 λ 取决于我们修改一个人的数据时，查询结果总共会改变多少？一般取 λ = 敏感度 / ε，即能满足ε-差分隐私

3.3.2 随机化回答

假设我向一组人问一个敏感的是非题，出于隐私，有的人可能不愿意给真实答案，

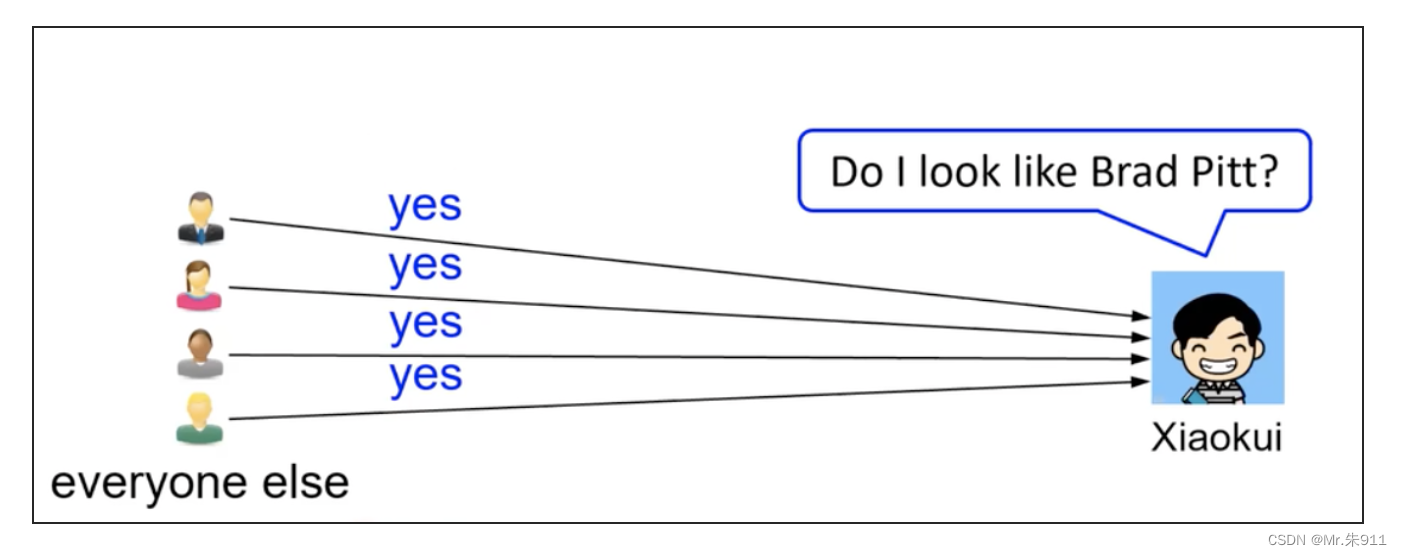
解决方案：让每个人在他的答案中加入噪声

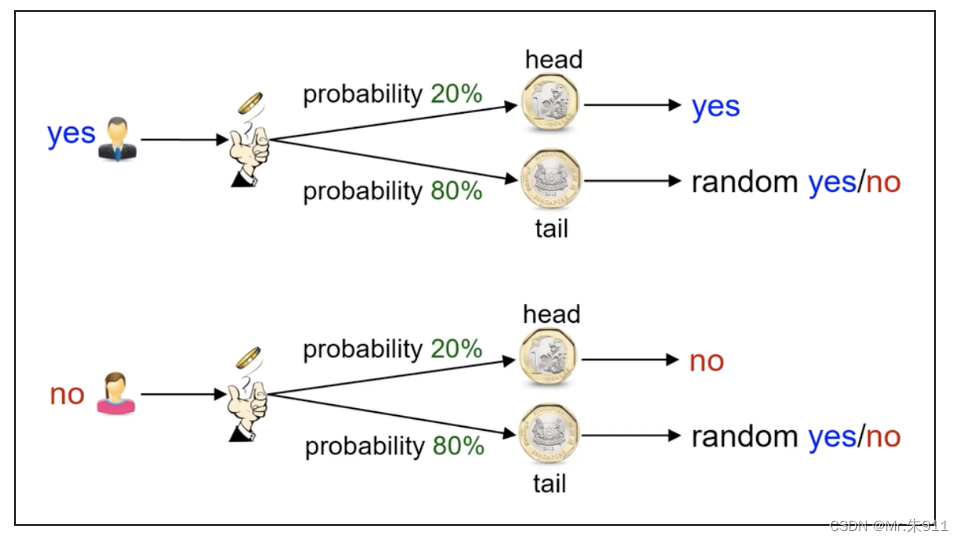
随机化回答可以满足 ε -差分隐私?
由于其随机性，攻击者并不能从随机化的输出反推出输入到底是“yes”还是“no”，只要根据ε 来调整随机化的概率即可。

• 假设有1000个人用随机化给了我回复

  • 当中有5500个yes和4500个no

• 每个人以80%概率给我假回复

  • 所有大致上总共有8000个假回复

  • 当中大致有4000个假yes和4000个假no

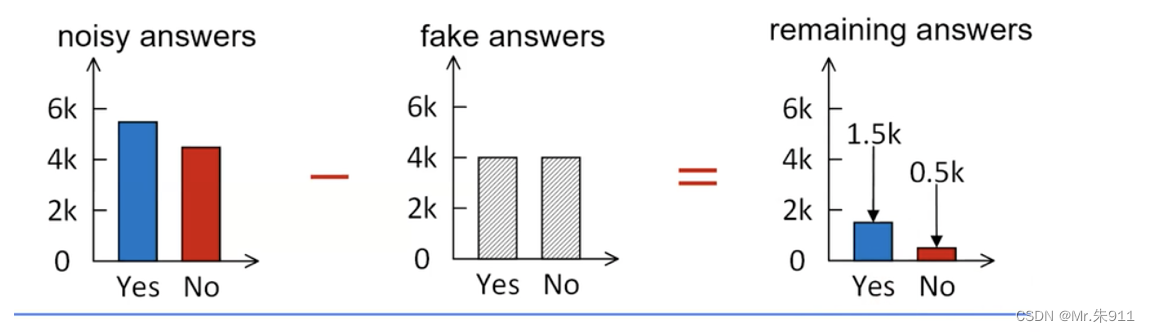
据此，可以推出剩下的真实回复大概有1500个yes和500个no，但无法反推出个体回复