【Mo 人工智能技术博客】采用 Python 机器学习预测足球比赛结果

采用 Python 机器学习预测足球比赛结果

足球是世界上最火爆的运动之一，世界杯期间也往往是球迷们最亢奋的时刻。比赛狂欢季除了炸出了熬夜看球的铁杆粉丝，也让足球竞猜也成了大家茶余饭后最热衷的话题。甚至连原来不怎么看足球的人，也是暗中努力恶补了很多足球相关知识，想通过赛事竞猜先赚一个小目标。今天我们将介绍如何用机器学习来预测足球比赛结果！

本 Chat 采用 Python 编程语言，使用人工智能建模平台 Mo 作为在线开发环境进行编程，通过获取 2000 年到 2018 年共 19 年英超的比赛数据，然后基于监督学习中逻辑回归模型、支持向量机模型和 XGBoost 模型，对英超比赛结果进行预测。

下面我们一起来看看预测英超比赛结果的机器学习步骤：

主要流程步骤

获取数据和读取数据的信息
数据清洗和预处理
特征工程
建立机器学习模型并进行预测
总结与展望

1. 获取数据和读取数据的信息

首先我们进入 Mo 工作台，创建一个空白项目，点击 开始开发 进入内嵌 JupyterLab 的 Notebook 开发环境。

enter image description here

接着我们需要在项目中上传数据集。

英超每年举办一个赛季，在每年的 8 月到第二年的 5 月进行，共有 20 支球队，实行主客场双循环赛制，每个赛季共 38 轮比赛（其中 19 场主场比赛，19 场客场比赛），每轮比赛共计 10 场比赛，所以每个赛季，英超共有 380 场比赛。

数据集地址

数据集中特征说明文档

如果您已经在 MO 平台新建项目，可以在平台直接导入数据集，流程如下：

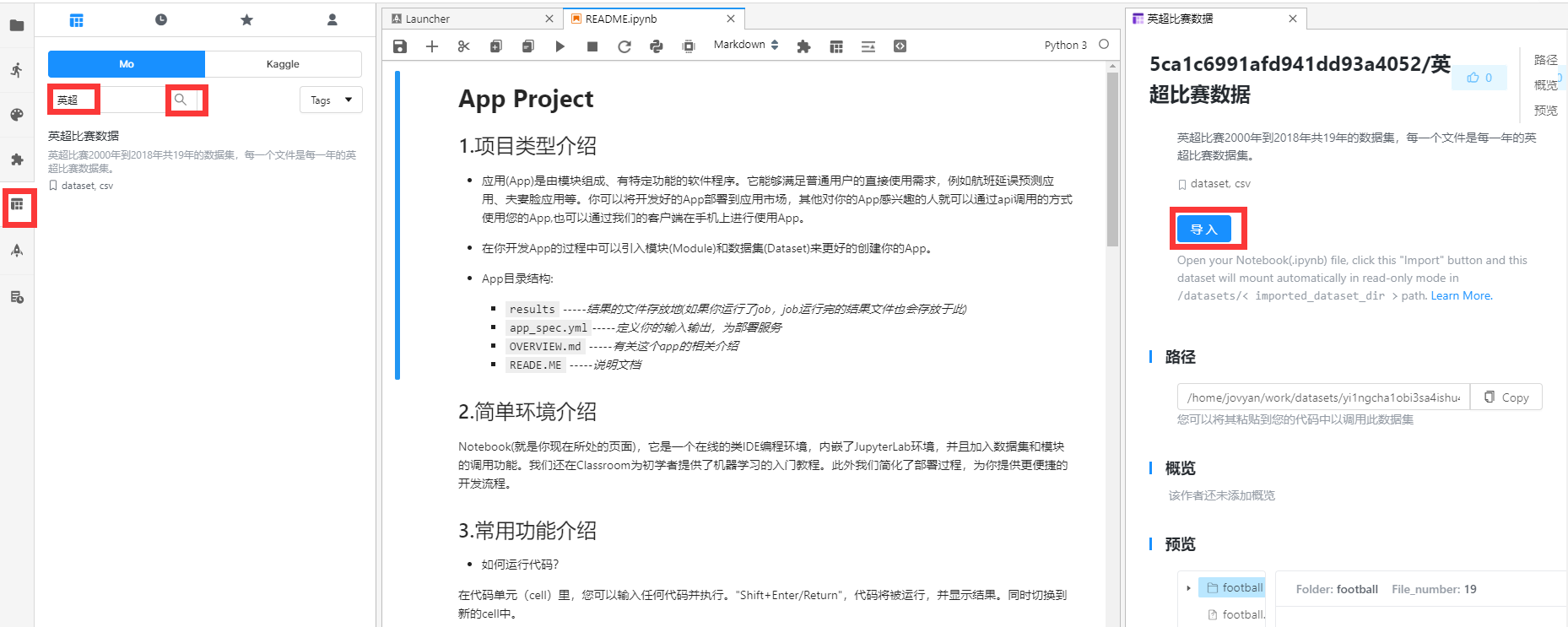
enter image description here

1.1 读取 csv 数据接口解释

采用 Pandas 读取、写入数据 API 汇总网址
读取 csv 数据一般采用 pandas.read_csv()：
pandas.read_csv(filepath_or_buffer, sep =‘,’ , delimiter = None)
- filepath_or_buffer:文件路径
- sep:指定分隔符，默认是逗号
- delimiter：定界符，备选分隔符（如果指定改参数，则sep失效）
- usecols: 指定读取的列名，列表形式

# 导入必须的包
import warnings
warnings.filterwarnings('ignore')  # 防止警告文件的包
import pandas as pd  # 数据分析包
import os
import matplotlib.pyplot as plt # 可视化包
import matplotlib
%matplotlib inline
import seaborn as sns  # 可视化包
from time import time
from sklearn.preprocessing import scale  # 标准化操作
from sklearn.model_selection import train_test_split  # 将数据集分成测试集和训练集
from sklearn.metrics import f1_score  # F1得分
import xgboost as xgb  # XGBoost模型
from sklearn.svm import SVC  ## 支持向量机分类模型
from sklearn.linear_model import LogisticRegression  # 逻辑回归模型
from sklearn.model_selection import GridSearchCV  # 超参数调参模块
from sklearn.metrics import make_scorer  # 模型评估
import joblib  # 模型的保存与加载模块

下面开始我们的表演：

# 获取地址中的所有文件
loc = './/football//' # 存放数据的路径
res_name = []  # 存放数据名的列表
filecsv_list = []  # 获取数据名后存放的列表
def file_name(file_name):# root:当前目录路径   dirs：当前目录下所有子目录   files：当前路径下所有非目录文件for root,dirs,files in os.walk(file_name):files.sort() # 排序，让列表里面的元素有顺序for i,file in enumerate(files):if os.path.splitext(file)[1] == '.csv':filecsv_list.append(file)res_name.append('raw_data_'+str(i+1))print(res_name)print(filecsv_list)
file_name(loc)

['raw_data_1', 'raw_data_2', 'raw_data_3', 'raw_data_4', 'raw_data_5', 'raw_data_6', 'raw_data_7', 'raw_data_8', 'raw_data_9', 'raw_data_10', 'raw_data_11', 'raw_data_12', 'raw_data_13', 'raw_data_14', 'raw_data_15', 'raw_data_16', 'raw_data_17', 'raw_data_18', 'raw_data_19']['2000-01.csv', '2001-02.csv', '2002-03.csv', '2003-04.csv', '2004-05.csv', '2005-06.csv', '2006-07.csv', '2007-08.csv', '2008-09.csv', '2009-10.csv', '2010-11.csv', '2011-12.csv', '2012-13.csv', '2013-14.csv', '2014-15.csv', '2015-16.csv', '2016-17.csv', '2017-18.csv', '2018-19.csv']

1.2 时间列表

获取每一年的数据后，将每一年的年份放入到 time_list 列表中：

time_list = [filecsv_list[i][0:4]  for i in range(len(filecsv_list))]
time_list

[‘2000’,‘2001’,‘2002’,‘2003’,‘2004’,‘2005’,‘2006’,‘2007’,‘2008’,‘2009’,‘2010’,‘2011’,‘2012’,‘2013’,‘2014’,‘2015’,‘2016’,‘2017’,‘2018’]

1.3 用 Pandas.read_csv() 接口读取数据

读取时将数据与 res_name 中的元素名一一对应。

for i in range(len(res_name)):res_name[i] = pd.read_csv(loc+filecsv_list[i],error_bad_lines=False)print('第%2s个文件是%s,数据大小为%s'%(i+1,filecsv_list[i],res_name[i].shape))

第 1个文件是2000-01.csv,数据大小为(380, 45)
第 2个文件是2001-02.csv,数据大小为(380, 48)
第 3个文件是2002-03.csv,数据大小为(316, 48)
第 4个文件是2003-04.csv,数据大小为(335, 57)
第 5个文件是2004-05.csv,数据大小为(335, 57)
第 6个文件是2005-06.csv,数据大小为(380, 68)
第 7个文件是2006-07.csv,数据大小为(380, 68)
第 8个文件是2007-08.csv,数据大小为(380, 71)
第 9个文件是2008-09.csv,数据大小为(380, 71)
第10个文件是2009-10.csv,数据大小为(380, 71)
第11个文件是2010-11.csv,数据大小为(380, 71)
第12个文件是2011-12.csv,数据大小为(380, 71)
第13个文件是2012-13.csv,数据大小为(380, 74)
第14个文件是2013-14.csv,数据大小为(380, 68)
第15个文件是2014-15.csv,数据大小为(381, 68)
第16个文件是2015-16.csv,数据大小为(380, 65)
第17个文件是2016-17.csv,数据大小为(380, 65)
第18个文件是2017-18.csv,数据大小为(380, 65)
第19个文件是2018-19.csv,数据大小为(304, 62)

1.4 删除特定文件的空值

经过查看第 15 个文件读取的第 381 行为空值，故采取删除行空值操作。

1.4.1 删除空值的接口

Pandas.dropna(axis=0，how=‘any’)
- axis： 0 表示是行；1表示是列
- how：'all’表示只去掉所有值均缺失的行、列；any表示只去掉有缺失值的行、列

1.4.2 接口运用

res_name[14] = res_name[14].dropna(axis=0,how='all')
res_name[14].tail()

	Div	Date	HomeTeam	AwayTeam	FTHG	FTAG	FTR	HTHG	HTR	...	BbAv<2.5	BbAH	BbAHh	BbMxAHH	BbAvAHH	BbMxAHA	BbAvAHA	PSCH	PSCD	PSCA
375	E0	24/05/15	Hull	Man United	0.0	0.0	D	0.0	D	...	1.99	25.0	0.50	1.76	1.71	2.27	2.19	3.20	3.76	2.27
376	E0	24/05/15	Leicester	QPR	5.0	1.0	H	2.0	H	...	2.41	28.0	-1.00	1.98	1.93	1.98	1.93	1.53	4.94	6.13
377	E0	24/05/15	Man City	Southampton	2.0	0.0	H	1.0	H	...	2.66	28.0	-1.00	2.00	1.94	2.03	1.93	1.60	4.35	6.00
378	E0	24/05/15	Newcastle	West Ham	2.0	0.0	H	0.0	D	...	2.25	25.0	-0.50	1.82	1.78	2.20	2.10	1.76	4.01	4.98
379	E0	24/05/15	Stoke	Liverpool	6.0	1.0	H	5.0	H	...	1.99	25.0	0.25	2.07	2.02	1.88	1.85	3.56	3.60	2.17

5 rows × 68 columns

1.5 删除行数不是 380 的文件名

考虑到英超一般是 19 个球队，每个球队需要打 20 场球，故把行数不是 380 的数据删除掉，并找到器原 CSV 文件一一对应。

for i in range(len(res_name),0,-1): # 采用从大到小的遍历方式，然后进行删除不满足条件的。if res_name[i-1].shape[0] != 380:key = 'res_name[' + str(i) + ']'print('删除的数据是：%s年的数据，文件名：%s大小是：%s'%(time_list[i-1],key,res_name[i-1].shape))res_name.pop(i-1)time_list.pop(i-1)continue

删除的数据是：2018年的数据，文件名：res_name[19]大小是：(304, 62)
删除的数据是：2004年的数据，文件名：res_name[5]大小是：(335, 57)
删除的数据是：2003年的数据，文件名：res_name[4]大小是：(335, 57)
删除的数据是：2002年的数据，文件名：res_name[3]大小是：(316, 48)

1.6 查看某一个数据集前n行数据

文件名.head(n)
- n:默认是5，想获取多少行数据就填写数字值。

读取数据前五行操作：

res_name[0].head()

	Div	Date	HomeTeam	AwayTeam	FTHG	FTAG	FTR	HTHG	HTAG	HTR	...	IWA	LBH	LBD	LBA	SBH	SBD	SBA	WHH	WHD	WHA
0	E0	19/08/00	Charlton	Man City	4	0	H	2	0	H	...	2.7	2.20	3.25	2.75	2.20	3.25	2.88	2.10	3.2	3.10
1	E0	19/08/00	Chelsea	West Ham	4	2	H	1	0	H	...	4.2	1.50	3.40	6.00	1.50	3.60	6.00	1.44	3.6	6.50
2	E0	19/08/00	Coventry	Middlesbrough	1	3	A	1	1	D	...	2.7	2.25	3.20	2.75	2.30	3.20	2.75	2.30	3.2	2.62
3	E0	19/08/00	Derby	Southampton	2	2	D	1	2	A	...	3.5	2.20	3.25	2.75	2.05	3.20	3.20	2.00	3.2	3.20
4	E0	19/08/00	Leeds	Everton	2	0	H	2	0	H	...	4.5	1.55	3.50	5.00	1.57	3.60	5.00	1.61	3.5	4.50

5 rows × 45 columns

读取数据前10行：

res_name[0].head(10)

	Div	Date	HomeTeam	AwayTeam	FTHG	FTAG	FTR	HTHG	HTAG	HTR	...	IWA	LBH	LBD	LBA	SBH	SBD	SBA	WHH	WHD	WHA
0	E0	19/08/00	Charlton	Man City	4	0	H	2	0	H	...	2.7	2.20	3.25	2.75	2.20	3.25	2.88	2.10	3.20	3.10
1	E0	19/08/00	Chelsea	West Ham	4	2	H	1	0	H	...	4.2	1.50	3.40	6.00	1.50	3.60	6.00	1.44	3.60	6.50
2	E0	19/08/00	Coventry	Middlesbrough	1	3	A	1	1	D	...	2.7	2.25	3.20	2.75	2.30	3.20	2.75	2.30	3.20	2.62
3	E0	19/08/00	Derby	Southampton	2	2	D	1	2	A	...	3.5	2.20	3.25	2.75	2.05	3.20	3.20	2.00	3.20	3.20
4	E0	19/08/00	Leeds	Everton	2	0	H	2	0	H	...	4.5	1.55	3.50	5.00	1.57	3.60	5.00	1.61	3.50	4.50
5	E0	19/08/00	Leicester	Aston Villa	0	0	D	0	0	D	...	2.5	2.35	3.20	2.60	2.25	3.25	2.75	2.40	3.25	2.50
6	E0	19/08/00	Liverpool	Bradford	1	0	H	0	0	D	...	8.0	1.35	4.00	8.00	1.36	4.00	8.00	1.33	4.00	8.00
7	E0	19/08/00	Sunderland	Arsenal	1	0	H	0	0	D	...	2.1	4.30	3.20	1.70	3.30	3.10	2.05	3.75	3.00	1.90
8	E0	19/08/00	Tottenham	Ipswich	3	1	H	2	1	H	...	4.7	1.45	3.60	6.50	1.50	3.50	6.50	1.44	3.60	6.50
9	E0	20/08/00	Man United	Newcastle	2	0	H	1	0	H	...	5.0	1.40	3.75	7.00	1.40	3.75	7.50	1.40	3.75	7.00

10 rows × 45 columns

通过以上2次操作，我们发现表格的第一行为各个特征的名称，最左边的一列为样本的序列号，一般都是从 0 开始；在这里也可以理解为每一行是一场比赛。 #### 1.7 查看某一个数据集后 5 行数据 - 文件名.tail()：用法与 head() 一样

读取最后 5 行操作：

res_name[0].tail()

	Div	Date	HomeTeam	AwayTeam	FTHG	FTAG	FTR	HTHG	HTAG	HTR	...	IWA	LBH	LBD	LBA	SBH	SBD	SBA	WHH	WHD	WHA
375	E0	19/05/01	Man City	Chelsea	1	2	A	1	1	D	...	1.65	4.0	3.60	1.67	4.20	3.40	1.70	4.00	3.1	1.80
376	E0	19/05/01	Middlesbrough	West Ham	2	1	H	2	1	H	...	3.20	1.8	3.25	3.75	1.90	3.20	3.50	1.83	3.4	3.50
377	E0	19/05/01	Newcastle	Aston Villa	3	0	H	2	0	H	...	2.90	2.4	3.25	2.50	2.38	3.30	2.50	2.25	3.4	2.60
378	E0	19/05/01	Southampton	Arsenal	3	2	H	0	1	A	...	2.35	2.5	3.25	2.37	2.63	3.25	2.30	2.62	3.5	2.20
379	E0	19/05/01	Tottenham	Man United	3	1	H	1	1	D	...	2.10	2.6	3.20	2.37	2.60	3.25	2.35	2.62	3.3	2.25

5 rows × 45 columns

读取最后 4 行操作：

res_name[0].tail(4)

	Div	Date	HomeTeam	AwayTeam	FTHG	FTAG	FTR	HTHG	HTAG	HTR	...	IWA	LBH	LBD	LBA	SBH	SBD	SBA	WHH	WHD	WHA
376	E0	19/05/01	Middlesbrough	West Ham	2	1	H	2	1	H	...	3.20	1.8	3.25	3.75	1.90	3.20	3.50	1.83	3.4	3.50
377	E0	19/05/01	Newcastle	Aston Villa	3	0	H	2	0	H	...	2.90	2.4	3.25	2.50	2.38	3.30	2.50	2.25	3.4	2.60
378	E0	19/05/01	Southampton	Arsenal	3	2	H	0	1	A	...	2.35	2.5	3.25	2.37	2.63	3.25	2.30	2.62	3.5	2.20
379	E0	19/05/01	Tottenham	Man United	3	1	H	1	1	D	...	2.10	2.6	3.20	2.37	2.60	3.25	2.35	2.62	3.3	2.25

4 rows × 45 columns

1.8 获取某一年主场队伍的名称

res_name[0]['HomeTeam'].unique()

array(['Charlton', 'Chelsea', 'Coventry', 'Derby', 'Leeds', 'Leicester','Liverpool', 'Sunderland', 'Tottenham', 'Man United', 'Arsenal','Bradford', 'Ipswich', 'Middlesbrough', 'Everton', 'Man City','Newcastle', 'Southampton', 'West Ham', 'Aston Villa'],dtype=object)

1.9 解析数据集列表头含义

数据集行数已经固定，一般都是 380 行，而列数可能每年统计指标有变化，不一定相等，而且我们也比较关心列数表表头。由于比较小，可以直接看数据集列数，这样比较快，也可以代码实现，找到最大的列数，然后获取列数的表头进行一般性介绍解释。

# 获取列表头最大的列数，然后获取器参数
shape_list = [res_name[i].shape[1] for i in range(len(res_name))]
for i in range(len(res_name)):if res_name[i].shape[1] == max(shape_list):print('%s年数据是有最大列数:%s,列元素表头：\n %s'%(time_list[i],max(shape_list),res_name[i].columns))

   2012年数据是有最大列数:74,列元素表头：Index(['Div', 'Date', 'HomeTeam', 'AwayTeam', 'FTHG', 'FTAG', 'FTR', 'HTHG','HTAG', 'HTR', 'Referee', 'HS', 'AS', 'HST', 'AST', 'HF', 'AF', 'HC','AC', 'HY', 'AY', 'HR', 'AR', 'B365H', 'B365D', 'B365A', 'BWH', 'BWD','BWA', 'GBH', 'GBD', 'GBA', 'IWH', 'IWD', 'IWA', 'LBH', 'LBD', 'LBA','PSH', 'PSD', 'PSA', 'WHH', 'WHD', 'WHA', 'SJH', 'SJD', 'SJA', 'VCH','VCD', 'VCA', 'BSH', 'BSD', 'BSA', 'Bb1X2', 'BbMxH', 'BbAvH', 'BbMxD','BbAvD', 'BbMxA', 'BbAvA', 'BbOU', 'BbMx>2.5', 'BbAv>2.5', 'BbMx<2.5','BbAv<2.5', 'BbAH', 'BbAHh', 'BbMxAHH', 'BbAvAHH', 'BbMxAHA', 'BbAvAHA','PSCH', 'PSCD', 'PSCA'],dtype='object')

我们看到数据包括 **Date（比赛的时间），Hometeam（主场队伍名），Awayteam（客场队伍名），FTHG（主场球队全场进球数），HTHG（主场球队半场进球数），FTR（全场比赛结果）**等等，更多关于数据集中特征信息可以参考数据集特征说明文档。

2. 数据清洗和预处理

我们挑选 Hometeam，Awayteam，FTHG，FTAG，FTR 这五列数据，作为我们的原始的特征数据，后面基于这些原始特征，我们再构造一些新的特征。

2.1 挑选信息列

HomeTeam: 主场球队名
AwayTeam: 客场球队名
FTHG: 全场主场球队进球数
FTAG: 全场客场球队进球数
FTR: 比赛结果 ( H= 主场赢, D= 平局, A= 客场赢)

# 将挑选的信息放在一个新的列表中
columns_req = ['HomeTeam','AwayTeam','FTHG','FTAG','FTR']
playing_statistics = []   # 创造处理后数据名存放处
playing_data = {}  # 键值对存储数据
for i in range(len(res_name)):playing_statistics.append('playing_statistics_'+str(i+1))playing_statistics[i] = res_name[i][columns_req]print(time_list[i],'playing_statistics['+str(i)+']',playing_statistics[i].shape)

2000 playing_statistics[0] (380, 5)
2001 playing_statistics[1] (380, 5)
2005 playing_statistics[2] (380, 5)
2006 playing_statistics[3] (380, 5)
2007 playing_statistics[4] (380, 5)
2008 playing_statistics[5] (380, 5)
2009 playing_statistics[6] (380, 5)
2010 playing_statistics[7] (380, 5)
2011 playing_statistics[8] (380, 5)
2012 playing_statistics[9] (380, 5)
2013 playing_statistics[10] (380, 5)
2014 playing_statistics[11] (380, 5)
2015 playing_statistics[12] (380, 5)
2016 playing_statistics[13] (380, 5)
2017 playing_statistics[14] (380, 5)

2.2 分析原始数据

我们首先预测所有主场球队全都胜利，然后预测所有的客场都会胜利，对结果进行对比分析:

2.2.1 统计所有主场球队都会胜利的准确率

def predictions_0(data):""" 当我们统计所有主场球队都赢，那么我们预测的结果是什么返回值是预测值和实际值"""predictions = []for _, game in data.iterrows():if game['FTR']=='H':predictions.append(1)else:predictions.append(0)# 返回预测结果return pd.Series(predictions)# 那我们对19年全部主场球队都赢的结果进行预测，获取预测的准确率。
avg_acc_sum = 0
for i in range(len(playing_statistics)):predictions = predictions_0(playing_statistics[i])acc=sum(predictions)/len(playing_statistics[i])avg_acc_sum += accprint("%s年数据主场全胜预测的准确率是%s"%(time_list[i],acc))
print('共%s年的平均准确率是：%s'%(len(playing_statistics),avg_acc_sum/len(playing_statistics)))

2000年数据主场全胜预测的准确率是0.4842105263157895
2001年数据主场全胜预测的准确率是0.4342105263157895
2005年数据主场全胜预测的准确率是0.5052631578947369
2006年数据主场全胜预测的准确率是0.4789473684210526
2007年数据主场全胜预测的准确率是0.4631578947368421
2008年数据主场全胜预测的准确率是0.45526315789473687
2009年数据主场全胜预测的准确率是0.5078947368421053
2010年数据主场全胜预测的准确率是0.4710526315789474
2011年数据主场全胜预测的准确率是0.45
2012年数据主场全胜预测的准确率是0.4368421052631579
2013年数据主场全胜预测的准确率是0.4710526315789474
2014年数据主场全胜预测的准确率是0.45263157894736844
2015年数据主场全胜预测的准确率是0.4131578947368421
2016年数据主场全胜预测的准确率是0.4921052631578947
2017年数据主场全胜预测的准确率是0.45526315789473687
共15年的平均准确率是：0.46473684210526317

2.2.2 统计所有客场球队都会胜利的准确率

def predictions_1(data):""" 当我们统计所有客场球队都赢，那么我们预测的结果是什么返回值是预测值和实际值"""predictions = []for _, game in data.iterrows():if game['FTR']=='A':predictions.append(1)else:predictions.append(0)# 返回预测结果return pd.Series(predictions)# 那我们对19年客场球队都赢的结果进行预测，获取预测的准确率。
for i in range(len(playing_statistics)):predictions = predictions_1(playing_statistics[i])acc=sum(predictions)/len(playing_statistics[i])print("%s年数据客场全胜预测的准确率是%s"%(time_list[i],acc))

2000年数据客场全胜预测的准确率是0.25
2001年数据客场全胜预测的准确率是0.3
2005年数据客场全胜预测的准确率是0.29210526315789476
2006年数据客场全胜预测的准确率是0.2631578947368421
2007年数据客场全胜预测的准确率是0.2736842105263158
2008年数据客场全胜预测的准确率是0.2894736842105263
2009年数据客场全胜预测的准确率是0.2394736842105263
2010年数据客场全胜预测的准确率是0.23684210526315788
2011年数据客场全胜预测的准确率是0.30526315789473685
2012年数据客场全胜预测的准确率是0.2789473684210526
2013年数据客场全胜预测的准确率是0.3236842105263158
2014年数据客场全胜预测的准确率是0.3026315789473684
2015年数据客场全胜预测的准确率是0.30526315789473685
2016年数据客场全胜预测的准确率是0.2868421052631579
2017年数据客场全胜预测的准确率是0.28421052631578947

综上比较：我们可以看出主场胜利的概率相对于输和平局来说，确实概率要大。

2.3 我们想知道 Arsenal 作为主场队伍时，他们的表现，如何求出 2005-06 所有比赛累计进球数 ?

我们知道 2005-06 年数据在 playing_statistics[2] 中：

def score(data):""" Arsenal作为主场队伍时，累计进球数 """scores=[]for _,game in data.iterrows():if game['HomeTeam']=='Arsenal':scores.append(game['FTHG'])return np.sum(scores)
Arsenal_score=score(playing_statistics[2])
print("Arsenal作为主场队伍在2005年时，累计进球数：%s"%(Arsenal_score))

Arsenal 作为主场队伍在2005年时，累计进球数：48

2.4 我们想知道各个球队作为主场队伍时，他们的表现如何 ?

先试试求 2005-06 所有比赛各个球队累计进球数。

print(playing_statistics[5].groupby('HomeTeam').sum()['FTHG'])

HomeTeam
Arsenal          31
Aston Villa      27
Blackburn        22
Bolton           21
Chelsea          33
Everton          31
Fulham           28
Hull             18
Liverpool        41
Man City         40
Man United       43
Middlesbrough    17
Newcastle        24
Portsmouth       26
Stoke            22
Sunderland       21
Tottenham        21
West Brom        26
West Ham         23
Wigan            17
Name: FTHG, dtype: int64

3. 特征工程

特征工程指的是把原始数据转变为模型的训练数据的过程，它的目的就是获取更好的训练数据特征，得到更好的训练模型。特征工程能使得模型的性能得到提升，有时甚至在简单的模型上也能取得不错的效果。特征工程在机器学习中占有非常重要的作用，一般认为括特征构建、特征提取、特征选择三大部分。

3.1 构造特征

因为这个比赛是一年一个赛季，是有先后顺序的，那我们就可以统计到截止到本场比赛之前，整个赛季内，主客场队伍的净胜球的数量。那么对于每一个赛季的每一周，都统计出每个球队到本周为止累计的进球数和丢球数之差，也就是净胜球的数量。

3.1.1 计算每个队周累计净胜球数量

处理后的数据，我们可以通过看某一年的某几条数据来体现，比如：05-06 年的后五条数据

def get_goals_diff(playing_stat):# 创建一个字典，每个 team 的 name 作为 keyteams = {}for i in playing_stat.groupby('HomeTeam').mean().T.columns:teams[i] = []# 对于每一场比赛for i in range(len(playing_stat)):# 全场比赛，主场队伍的进球数HTGS = playing_stat.iloc[i]['FTHG']# 全场比赛，客场队伍的进球数ATGS = playing_stat.iloc[i]['FTAG']# 把主场队伍的净胜球数添加到 team 这个 字典中对应的主场队伍下teams[playing_stat.iloc[i].HomeTeam].append(HTGS-ATGS)# 把客场队伍的净胜球数添加到 team 这个 字典中对应的客场队伍下teams[playing_stat.iloc[i].AwayTeam].append(ATGS-HTGS)# 创建一个 GoalsDifference 的 dataframe# 行是 team 列是 matchweek,# 39解释：19个球队，每个球队分主场客场2次，共38个赛次，但是range取不到最后一个值，故38+1=39GoalsDifference = pd.DataFrame(data=teams, index = [i for i in range(1,39)]).TGoalsDifference[0] = 0# 累加每个队的周比赛的净胜球数for i in range(2,39):GoalsDifference[i] = GoalsDifference[i] + GoalsDifference[i-1]return GoalsDifferencedef get_gss(playing_stat):# 得到净胜球数统计GD = get_goals_diff(playing_stat)j = 0#  主客场的净胜球数HTGD = []ATGD = []# 全年一共380场比赛for i in range(380):ht = playing_stat.iloc[i].HomeTeamat = playing_stat.iloc[i].AwayTeamHTGD.append(GD.loc[ht][j])ATGD.append(GD.loc[at][j])if ((i + 1)% 10) == 0:j = j + 1# 把每个队的 HTGD ATGD 信息补充到 dataframe 中playing_stat.loc[:,'HTGD'] = HTGDplaying_stat.loc[:,'ATGD'] = ATGDreturn playing_statfor i in range(len(playing_statistics)):playing_statistics[i] = get_gss(playing_statistics[i])####  查看构造特征后的05-06年的后五条数据
playing_statistics[2].tail()

	HomeTeam	AwayTeam	FTHG	FTAG	FTR	HTGD	ATGD
375	Fulham	Middlesbrough	1	0	H	-11	-9
376	Man United	Charlton	4	0	H	34	-10
377	Newcastle	Chelsea	1	0	H	4	51
378	Portsmouth	Liverpool	1	3	A	-23	30
379	West Ham	Tottenham	2	1	H	-4	16

通过以上数据：我们发现 376 行数据的特点，截止到这一场比赛之前，本赛季主场曼联队的净胜球数是 34 ，客场查尔顿队的净胜球数是 -10 。

3.1.2 统计主客场队伍到当前比赛周的累计得分

统计整个赛季主客场队伍截止到当前比赛周的累计得分。一场比赛胜利计 3 分，平局计 1 分，输了计 0 分。我们根据本赛季本周之前的比赛结果来统计这个值。我们继续观看 05-06 年的后五条数据：

# 把比赛结果转换为得分，赢得三分，平局得一分，输不得分
def get_points(result):if result == 'W':return 3elif result == 'D':return 1else:return 0def get_cuml_points(matchres):matchres_points = matchres.applymap(get_points)for i in range(2,39):matchres_points[i] = matchres_points[i] + matchres_points[i-1]matchres_points.insert(column =0, loc = 0, value = [0*i for i in range(20)])return matchres_pointsdef get_matchres(playing_stat):# 创建一个字典，每个 team 的 name 作为 keyteams = {}for i in playing_stat.groupby('HomeTeam').mean().T.columns:teams[i] = []# 把比赛结果分别记录在主场队伍和客场队伍中# H：代表 主场 赢# A：代表 客场 赢# D：代表 平局for i in range(len(playing_stat)):if playing_stat.iloc[i].FTR == 'H':# 主场 赢，则主场记为赢，客场记为输teams[playing_stat.iloc[i].HomeTeam].append('W')teams[playing_stat.iloc[i].AwayTeam].append('L')elif playing_stat.iloc[i].FTR == 'A':# 客场 赢，则主场记为输，客场记为赢teams[playing_stat.iloc[i].AwayTeam].append('W')teams[playing_stat.iloc[i].HomeTeam].append('L')else:# 平局teams[playing_stat.iloc[i].AwayTeam].append('D')teams[playing_stat.iloc[i].HomeTeam].append('D')return pd.DataFrame(data=teams, index = [i for i in range(1,39)]).Tdef get_agg_points(playing_stat):matchres = get_matchres(playing_stat)cum_pts = get_cuml_points(matchres)HTP = []ATP = []j = 0for i in range(380):ht = playing_stat.iloc[i].HomeTeamat = playing_stat.iloc[i].AwayTeamHTP.append(cum_pts.loc[ht][j])ATP.append(cum_pts.loc[at][j])if ((i + 1)% 10) == 0:j = j + 1# 主场累计得分playing_stat.loc[:,'HTP'] = HTP# 客场累计得分playing_stat.loc[:,'ATP'] = ATPreturn playing_statfor i in range(len(playing_statistics)):playing_statistics[i] = get_agg_points(playing_statistics[i])#查看构造特征后的05-06年的后五条数据
playing_statistics[2].tail()

	HomeTeam	AwayTeam	FTHG	FTAG	FTR	HTGD	ATGD	HTP	ATP
375	Fulham	Middlesbrough	1	0	H	-11	-9	45	45
376	Man United	Charlton	4	0	H	34	-10	80	47
377	Newcastle	Chelsea	1	0	H	4	51	55	91
378	Portsmouth	Liverpool	1	3	A	-23	30	38	79
379	West Ham	Tottenham	2	1	H	-4	16	52	65

我们处理得到 HTP (本赛季主场球队截止到本周的累计得分)， ATP (本赛季客场球队截止到本周的累计得分)。
我们再看 376 行，截止到这一场比赛，本赛季，曼联队一共积了80分，查尔顿队积了 47 分。

3.1.3 统计某支队伍最近三场比赛的表现

前面我们构造的特征反映了一只队伍本赛季的历史总表现，我们看看队伍在最近三场比赛的表现。
我们用:

HM1 代表主场球队上一次比赛的输赢，

AM1 代表客场球队上一次比赛是输赢。

同理，HM2 AM2 就是上上次比赛的输赢， HM3 AM3 就是上上上次比赛的输赢。

我们继续观看处理后 05-06 年的后 5 五条数据：

def get_form(playing_stat,num):form = get_matchres(playing_stat)form_final = form.copy()for i in range(num,39):form_final[i] = ''j = 0while j < num:form_final[i] += form[i-j]j += 1return form_finaldef add_form(playing_stat,num):form = get_form(playing_stat,num)# M 代表 unknown， 因为没有那么多历史h = ['M' for i in range(num * 10)]a = ['M' for i in range(num * 10)]j = numfor i in range((num*10),380):ht = playing_stat.iloc[i].HomeTeamat = playing_stat.iloc[i].AwayTeampast = form.loc[ht][j]h.append(past[num-1])past = form.loc[at][j]a.append(past[num-1])if ((i + 1)% 10) == 0:j = j + 1playing_stat['HM' + str(num)] = hplaying_stat['AM' + str(num)] = areturn playing_statdef add_form_df(playing_statistics):playing_statistics = add_form(playing_statistics,1)playing_statistics = add_form(playing_statistics,2)playing_statistics = add_form(playing_statistics,3)return playing_statisticsfor i in range(len(playing_statistics)):playing_statistics[i] = add_form_df(playing_statistics[i])#查看构造特征后的05-06年的后5五条数据
playing_statistics[2].tail()

	HomeTeam	AwayTeam	FTHG	FTAG	FTR	HTGD	ATGD	HTP	ATP	HM1	AM1	HM2	AM2	HM3	AM3
375	Fulham	Middlesbrough	1	0	H	-11	-9	45	45	L	D	W	D	W	L
376	Man United	Charlton	4	0	H	34	-10	80	47	D	L	L	L	W	W
377	Newcastle	Chelsea	1	0	H	4	51	55	91	D	L	W	W	W	W
378	Portsmouth	Liverpool	1	3	A	-23	30	38	79	W	W	W	W	L	W
379	West Ham	Tottenham	2	1	H	-4	16	52	65	W	W	L	D	L	L

3.1.4 加入比赛周特征（第几个比赛周）

然后我们把比赛周的信息也放在里面，也就是这一场比赛发生在第几个比赛周。
特征构造后的结果，我们可以直接查看 05-06 年的后 5 条数据:

def get_mw(playing_stat):j = 1MatchWeek = []for i in range(380):MatchWeek.append(j)if ((i + 1)% 10) == 0:j = j + 1playing_stat['MW'] = MatchWeekreturn playing_statfor i in range(len(playing_statistics)):playing_statistics[i] = get_mw(playing_statistics[i])#查看构造特征后的05-06年的后五条数据
playing_statistics[2].tail()

	HomeTeam	AwayTeam	FTHG	FTAG	FTR	HTGD	ATGD	HTP	ATP	HM1	AM1	HM2	AM2	HM3	AM3	MW
375	Fulham	Middlesbrough	1	0	H	-11	-9	45	45	L	D	W	D	W	L	38
376	Man United	Charlton	4	0	H	34	-10	80	47	D	L	L	L	W	W	38
377	Newcastle	Chelsea	1	0	H	4	51	55	91	D	L	W	W	W	W	38
378	Portsmouth	Liverpool	1	3	A	-23	30	38	79	W	W	W	W	L	W	38
379	West Ham	Tottenham	2	1	H	-4	16	52	65	W	W	L	D	L	L	38

3.1.5 合并比赛的信息

我们打算把数据集比赛的信息都合并到一个表里面，然后我们把我们刚才计算得到的这些得分数据，净胜球数据除以周数，就得到了周平均后的值。结果就可以通过查看构造特征后数据集的后 5 条数据。

# 将各个DataFrame表合并在一张表中
playing_stat = pd.concat(playing_statistics, ignore_index=True)# HTGD, ATGD ,HTP, ATP的值 除以 week 数，得到平均分
cols = ['HTGD','ATGD','HTP','ATP']
playing_stat.MW = playing_stat.MW.astype(float)
for col in cols:playing_stat[col] = playing_stat[col] / playing_stat.MW#查看构造特征后数据集的后5五条数据
playing_stat.tail()

	HomeTeam	AwayTeam	FTHG	FTAG	FTR	HTGD	ATGD	HTP	ATP	HM1	AM1	HM2	AM2	HM3	AM3	MW
5695	Newcastle	Chelsea	3.0	0.0	H	-0.289474	0.710526	1.078947	1.842105	L	D	L	W	L	W	38.0
5696	Southampton	Man City	0.0	1.0	A	-0.473684	2.052632	0.947368	2.552632	W	W	D	D	W	W	38.0
5697	Swansea	Stoke	1.0	2.0	A	-0.710526	-0.894737	0.868421	0.789474	L	L	L	D	L	D	38.0
5698	Tottenham	Leicester	5.0	4.0	H	0.973684	-0.078947	1.947368	1.236842	W	W	L	L	W	L	38.0
5699	West Ham	Everton	3.0	1.0	H	-0.578947	-0.315789	1.026316	1.289474	D	D	W	W	L	W	38.0

我们看到数据集最后一行的行数是 5699 ，加上第一行为 0 行，则一共 5700 条数据；我们总共统计了 15 年的数据，每一年有 380 条数据，计算后发现我们统计后的数据集大小是准确的。

3.2 删除某些数据

前面我们根据初始的特征构造出了很多的特征。这其中有一部分是中间的特征，我们需要把这些中间特征抛弃掉。因为前三周的比赛，每个队的历史胜负信息不足，所以我们打算弃掉前三周的数据。

# 抛弃前三周的比赛
playing_stat = playing_stat[playing_stat.MW > 3]
playing_stat.drop(['HomeTeam', 'AwayTeam', 'FTHG', 'FTAG', 'MW'],1, inplace=True)#我们查看下此时的数据的特征
playing_stat.keys()

Index(['FTR', 'HTGD', 'ATGD', 'HTP', 'ATP', 'HM1', 'AM1', 'HM2', 'AM2', 'HM3','AM3'], dtype='object')

3.3 分析我们构造的数据

在前面，我们计算了每一的年主客场的胜率，现在我们看看有效数据中，是主场胜利的多呢，还是客场胜利的多呢？

# 比赛总数
n_matches = playing_stat.shape[0]# 特征数
n_features = playing_stat.shape[1] - 1# 主场获胜的数目
n_homewins = len(playing_stat[playing_stat.FTR == 'H'])# 主场获胜的比例
win_rate = (float(n_homewins) / (n_matches)) * 100# Print the results
print("比赛总数: {}".format(n_matches))
print("总特征数: {}".format(n_features))
print("主场胜利数: {}".format(n_homewins))
print("主场胜率: {:.2f}%".format(win_rate))

比赛总数: 5250
总特征数: 10
主场胜利数: 2451
主场胜率: 46.69%

通过统计结果看到：我们主场胜率 46.69% 与我们第 2.2.1 小节原始数据分析的结果是一致的，说明我们前面构造的特征是有效的，比较贴近实际的。

3.4 解决样本不均衡问题

通过构造特征之后，发现主场获胜的比例接近 50% ，所以对于这个三分类的问题，标签比例是不均衡的。

我们把它简化为二分类问题，也就是主场球队会不会胜利，这也是一种解决标签比例不均衡的问题的方法。

# 定义 target ，也就是否 主场赢
def only_hw(string):if string == 'H':return 'H'else:return 'NH'
playing_stat['FTR'] = playing_stat.FTR.apply(only_hw)

3.5 将数据分为特征值和标签值

# 把数据分为特征值和标签值
X_all = playing_stat.drop(['FTR'],1)
y_all = playing_stat['FTR']
# 特征值的长度
len(X_all)

3.6 数据归一化、标准化

我们对所有比赛的特征 HTP 进行最大最小值归一化。

def convert_1(data):max=data.max()min=data.min()return (data-min)/(max-min)
r_data=convert_1(X_all['HTGD'])

# 数据标准化
from sklearn.preprocessing import scale
cols = [['HTGD','ATGD','HTP','ATP']]
for col in cols:X_all[col] = scale(X_all[col])

3.7 转换特征数据类型

# 把这些特征转换成字符串类型
X_all.HM1 = X_all.HM1.astype('str')
X_all.HM2 = X_all.HM2.astype('str')
X_all.HM3 = X_all.HM3.astype('str')
X_all.AM1 = X_all.AM1.astype('str')
X_all.AM2 = X_all.AM2.astype('str')
X_all.AM3 = X_all.AM3.astype('str')def preprocess_features(X):'''把离散的类型特征转为哑编码特征 '''output = pd.DataFrame(index = X.index)for col, col_data in X.iteritems():if col_data.dtype == object:col_data = pd.get_dummies(col_data, prefix = col)output = output.join(col_data)return outputX_all = preprocess_features(X_all)
print("Processed feature columns ({} total features):\n{}".format(len(X_all.columns), list(X_all.columns)))

Processed feature columns (22 total features):
['HTGD', 'ATGD', 'HTP', 'ATP', 'HM1_D', 'HM1_L', 'HM1_W', 'AM1_D', 'AM1_L', 'AM1_W', 'HM2_D', 'HM2_L', 'HM2_W', 'AM2_D', 'AM2_L', 'AM2_W', 'HM3_D', 'HM3_L', 'HM3_W', 'AM3_D', 'AM3_L', 'AM3_W']

# 预览处理好的数据
print("\nFeature values:")
display(X_all.head())

Feature values:

	HTGD	ATGD	HTP	ATP	HM1_D	HM1_L	AM1_D	AM1_W	...	AM2_L	AM2_W	HM3_W	AM3_D	AM3_L
30	0.724821	0.339985	-0.043566	-0.603098	1	0	1	0	...	0	1	1	0	1
31	-0.702311	-1.088217	-1.097731	-2.192828	0	1	1	0	...	1	0	1	0	1
32	0.011255	0.339985	-0.570649	-0.603098	0	1	1	0	...	0	1	1	0	1
33	-0.345528	-0.374116	-1.097731	-1.662918	0	1	1	0	...	1	0	1	1	0
34	0.011255	1.054086	-0.570649	0.456723	1	0	0	1	...	0	1	1	0	1

5 rows × 22 columns

3.8 皮尔逊相关热力图

我们生成一些特征的相关图，以查看特征与特征之间的相关性。为此，我们将利用 Seaborn 绘图软件包，使我们能够非常方便地绘制热力图，如下所示：

import matplotlib.pyplot as plt
import seaborn as sns
# 防止中文出现错误
plt.rcParams['font.sans-serif']=['SimHei'] 
plt.rcParams['axes.unicode_minus']=False
#制成皮尔森热图
#把标签映射为0和1
y_all=y_all.map({'NH':0,'H':1})
#合并特征集和标签
train_data=pd.concat([X_all,y_all],axis=1)
colormap = plt.cm.RdBu
plt.figure(figsize=(21,18))
plt.title('Pearson Correlation of Features', y=1.05, size=15)
sns.heatmap(train_data.astype(float).corr(),linewidths=0.1,vmax=1.0,square=True, cmap=colormap, linecolor='white', annot=True)

<matplotlib.axes._subplots.AxesSubplot at 0x211ffda5860>

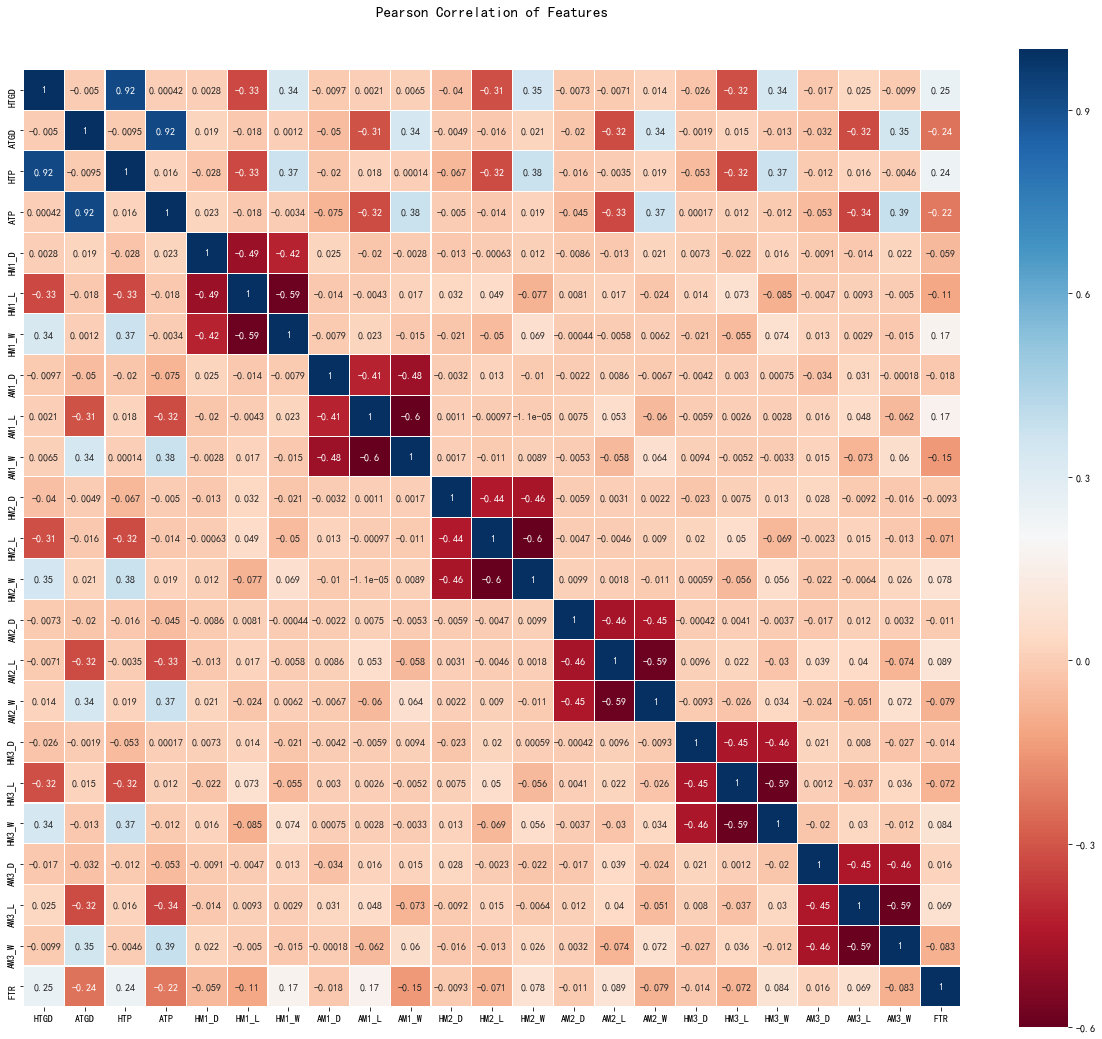
enter image description here

通过上图我们可以看出特征 HTP 特征和 HTGD 特征相关性很强，同样 ATP 特征和 ATGD 特征相关性很强，可以表明多重共线性的情况。这个我们也很容易理解，主场周平均得分数越高，那么主场周平均净胜球数也同样越高。如果我们考虑这些变量，我们可以得出结论，它们给出了几乎相同的信息，因此实际上发生了多重共线性，这里我们会考虑删除 HTP 和 ‘ATP’ 这两个特征，保留 HTGD 和 ATGD 这两个特征。皮尔森热图非常适合检测这种情况，并且在特征工程中，它们是必不可少的工具。同时，我们也可以看出上上上次球队的比赛结果对目前比赛的结果影响较小，这里我们考虑保留这些特征。

考虑到样本集特征 HTP 和 HTGD，ATP 和 ATGD 的相关性都超过了 90% ，故我们删除特征 HTP , ATP ：

X_all=X_all.drop(['HTP','ATP'],axis=1)

看看与FTR最相关的10个特征

#FTR correlation matrix
plt.figure(figsize=(14,12))
k = 10 # number of variables for heatmap
cols = abs(train_data.astype(float).corr()).nlargest(k, 'FTR')['FTR'].index
cm = np.corrcoef(train_data[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()

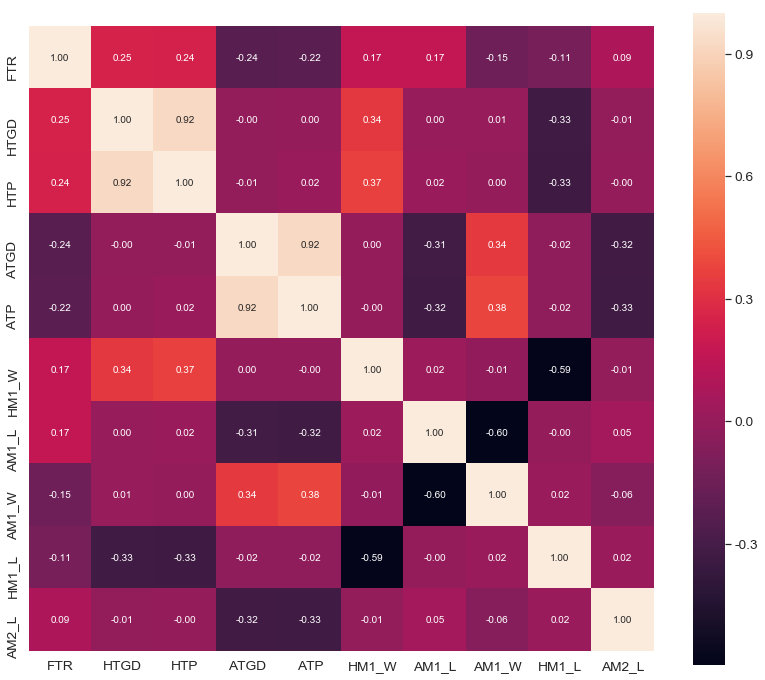
enter image description here

我们可以看出最相关的特征是 HTGD ，表明一个球队主场周平均净胜球数越高，他们赢的概率也就越大。

4.建立机器学习模型并进行预测

4.1 切分数据

将数据集随机分成为训练集和测试集，并返回划分好的训练集测试集样本和训练集测试集标签。我们直接采用 train_test_split 接口进行处理。

4.1.1 train_test_split API 接口介绍

X_train, X_test, y_train, y_test =cross_validation.train_test_split(train_data,train_target,test_size=0.3, random_state=0)
参数解释：
- train_data：被划分的样本特征集
- train_target：被划分的样本标签
- test_size：如果是浮点数，在0-1之间，表示样本占比；如果是整数的话就是样本的数量
- random_state：是随机数的种子。
返回值解释：
- x_train：训练集特征值
- x_test：测试集特征值
- y_train：训练集目标值
- y_test：测试集目标值

随机数种子：其实就是该组随机数的编号，在需要重复试验的时候，保证得到一组一样的随机数。比如你每次都填1，其他参数一样的情况下你得到的随机数组是一样的。但填0或不填，每次都会不一样。随机数的产生取决于种子，随机数和种子之间的关系遵从以下两个规则：种子不同，产生不同的随机数；种子相同，即使实例不同也产生相同的随机数。

4.1.2 代码处理分割数据

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_all, y_all,test_size = 0.3,random_state = 2,stratify = y_all)

4.2 相关模型及其接口介绍

下面我们分别使用逻辑回归、支持向量机和 XGBoost 这三种不同的模型，来看看他们的表现。我们先定义一些辅助函数，记录模型的训练时长和评估时长，计算模型的准确率和 f1 分数。我们首先介绍一下这三个模型联系与区别和相关的接口：

4.2.1 逻辑回归介绍

逻辑回归模型是：假设数据服从伯努利分布,通过极大化似然函数的方法，运用梯度下降来求解参数，来达到将数据二分类的目的。该模型的主要优点是解释性比较好；如果特征工程做得好，模型效果也非常不错；训练速度也比较快；输出结果也很容易调整。但是该模型的缺点也很突出，比如：准确率不是很高，比较难处理数据不均衡问题等。

4.2.2 逻辑回归模型接口介绍

API：sklearn.linear_model.LogisticRegression(penalty=‘l2’, dual=False, tol=0.0001, C=1.0,fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None,solver=‘liblinear’, max_iter=100, multi_class=‘ovr’, verbose=0,warm_start=False, n_jobs=1)

主要参数解析：
- penalty：正则化参数，l1 or l2, default: l2；
- C：正则化系数λ的倒数，default: 1.0；
- fit_intercept : 是否存在截距, default: True
- solver：损失函数的优化方法，有以下四种可供选择{newton-cg, lbfgs, liblinear,sag}, default: liblinear
- multi_class：分类方式选择，一般有{ovr, multinomial}, default:ovr；
- class_weight：类型权重参数，默认为None
- random_state：随机数种子，默认为无
- tol：迭代终止判据的误差范围
- n_jobs：并行数，为-1时跟CPU核数一致，默认值为1。
以上是主要参数的简单解析，如果大家想深入了解，可以参看官方网址。

4.2.3 支持向量机介绍

SVM(Support Vector Machine) 是一种二类分类模型。它的基本模型是在特征空间中寻找间隔最大化的分离超平面的线性分类器。

（1）当训练样本线性可分时，通过硬间隔最大化，学习一个线性分类器，即线性可分支持向量机；
（2）当训练数据近似线性可分时，引入松弛变量，通过软间隔最大化，学习一个线性分类器，即线性支持向量机；
（3）当训练数据线性不可分时，通过使用核技巧及软间隔最大化，学习非线性支持向量机。

4.2.4 支持向量机分类模型API

sklearn.svm.SVC(C=1.0,kernel=‘rbf’,degree=3,gamma=‘auto’,coef0=0.0,shrinking=True,probability=False,tol=0.001,cache_size=200,class_weight=None,verbose=False,max_iter=-1,decision_function_shape=None,random_state=None)

主要参数解析：
- C：C-SVC的惩罚参数C，默认值是1.0。C越大，相当于惩罚松弛变量，希望松弛变量接近0，即对误分类的惩罚增大，趋向于对训练集全分对的情况，这样对训练集测试时准确率很高，但泛化能力弱。C值小，对误分类的惩罚减小，允许容错，将他们当成噪声点，泛化能力较强。
- kernel ：核函数，默认是rbf，可以是‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’
  - 0 – 线性：u’v
  - 1 – 多项式：(gamma*u’*v + coef0)^degree
  - 2 – RBF函数：exp(-gamma|u-v|^2)
  - 3 –sigmoid：tanh(gamma*u’*v + coef0)
- degree ：多项式poly函数的维度，默认是3，选择其他核函数时会被忽略。
- gamma ：rbf,poly 和sigmoid的核函数参数。默认是auto，则会选择1/n_features
- coef0 ：核函数的常数项。对于poly和 sigmoid有用。
- max_iter ：最大迭代次数。-1为无限制。
- decision_function_shape ：ovo, ovr or None, default=None。

主要调节的参数有：C、kernel、degree、gamma、coef0；参数详解请参考官网。

4.2.5 XGBoost 原理介绍

XGBoost 是 Boosting算法的其中一种， Boosting 算法的思想是许多弱分类器集成在一起，形成一个强分类器，基本原理是下一棵决策树输入样本会与前面决策树的训练和预测相关。以为 XGBoost 是一种提升树模型，所以他是将许多树模型集成在一起，形成一个很强的分类器。而所用到的树模型则是 CART 回归树模型。

4.2.6 XGBoost 接口介绍

XGBoost.XGBRegressor(max_depth=3, learning_rate=0.1, n_estimators=100, silent=True, objective=‘reg:linear’, booster=‘gbtree’, n_jobs=1, nthread=None, gamma=0, min_child_weight=1, max_delta_step=0, subsample=1, colsample_bytree=1, colsample_bylevel=1, reg_alpha=0, reg_lambda=1, scale_pos_weight=1, base_score=0.5, random_state=0, seed=None, missing=None, **kwargs)

主要参数解析：
- booster：模型类别，主要有2种，gbtree 和 gbliner，默认是： gbtree ；
- nthread：使用 CPU 个数，为 -1 时表示使用全部 CPU 进行并行运算（默认），等于 1 时表示使用1个 CPU 进行运算；
- scale_pos_weight：正样本的权重，在二分类任务中，当正负样本比例失衡时，设置正样本的权重，模型效果更好。例如，当正负样本比例为 1:10 时，scale_pos_weight=10；
- n_estimatores：总共迭代的次数，即决策树的个数；
- early_stopping_rounds：在验证集上，当连续n次迭代，分数没有提高后，提前终止训练
- max_depth：树的深度，默认值为6，典型值3-10；
- min_child_weight：值越大，越容易欠拟合；值越小，越容易过拟合（值较大时，避免模型学习到局部的特殊样本），默认为1；
- learning_rate：学习率，控制每次迭代更新权重时的步长，默认0.3；
- gamma：惩罚项系数，指定节点分裂所需的最小损失函数下降值；
- alpha：L1 正则化系数，默认为 1 ;
- lambda：L2 正则化系数，默认为 1 ;
- seed：随机种子。

如想详细学习该 API ，可以参考官网网址。

4.3 建立机器学习模型并评估

4.3.1 建立模型

from time import time
from sklearn.metrics import f1_scoredef train_classifier(clf, X_train, y_train):''' 训练模型 '''# 记录训练时长start = time()clf.fit(X_train, y_train)end = time()print("训练时间 {:.4f} 秒".format(end - start))def predict_labels(clf, features, target):''' 使用模型进行预测 '''# 记录预测时长start = time()y_pred = clf.predict(features)end = time()print("预测时间 in {:.4f} 秒".format(end - start))return f1_score(target, y_pred, pos_label=1), sum(target == y_pred) / float(len(y_pred))def train_predict(clf, X_train, y_train, X_test, y_test):''' 训练并评估模型 '''# Indicate the classifier and the training set sizeprint("训练 {} 模型，样本数量 {}。".format(clf.__class__.__name__, len(X_train)))# 训练模型train_classifier(clf, X_train, y_train)# 在测试集上评估模型f1, acc = predict_labels(clf, X_train, y_train)print("训练集上的 F1 分数和准确率为: {:.4f} , {:.4f}。".format(f1 , acc))f1, acc = predict_labels(clf, X_test, y_test)print("测试集上的 F1 分数和准确率为: {:.4f} , {:.4f}。".format(f1 , acc))

4.3.2 分别初始化，训练和评估模型

import xgboost as xgb
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC# 分别建立三个模型
clf_A = LogisticRegression(random_state = 42)
clf_B = SVC(random_state = 42, kernel='rbf',gamma='auto')
clf_C = xgb.XGBClassifier(seed = 42)train_predict(clf_A, X_train, y_train, X_test, y_test)
print('')
train_predict(clf_B, X_train, y_train, X_test, y_test)
print('')
train_predict(clf_C, X_train, y_train, X_test, y_test)
print('')

训练 LogisticRegression 模型，样本数量 3675。
训练时间 0.0050 秒
预测时间 in 0.0010 秒
训练集上的 F1 分数和准确率为: 0.6232 , 0.6648。
预测时间 in 0.0010 秒
测试集上的 F1 分数和准确率为: 0.6120 , 0.6457。训练 SVC 模型，样本数量 3675。
训练时间 0.5755 秒
预测时间 in 0.3620 秒
训练集上的 F1 分数和准确率为: 0.6152 , 0.6746。
预测时间 in 0.1486 秒
测试集上的 F1 分数和准确率为: 0.5858 , 0.6400.训练 XGBClassifier 模型，样本数量 3675. . .
训练时间 0.4079 秒
预测时间 in 0.0110 秒
训练集上的 F1 分数和准确率为: 0.6652 , 0.7067.
预测时间 in 0.0060 秒
测试集上的 F1 分数和准确率为: 0.5844 , 0.6279。

通过运行结果，我们发现：

在训练时间上，逻辑回归耗时最短，XGBoost 耗时最长，为 2 秒多。
在预测时间上，逻辑回归耗时最短，支持向量机耗时最长。
在训练集上 F1 分数方面，**XGBoost **得分最高，支持向量机得分最低，但是差距不是很大。
在训练集上准确率方面分析，XGBoost得分最高，逻辑回归最低。
在测试集上 F1 分数方面分析，逻辑回归的最好，其余两个模型基本相等，相对较低。
在测试集上准确率方面分析，逻辑回归和支持向量机 2 个模型基本相等，稍微比 XBGoost 高一点。

4.4 超参数调整

我们使用 sklearn 的 GridSearch 来进行超参数调参。

from sklearn.model_selection import GridSearchCV
from sklearn.metrics import make_scorer
import xgboost as xgb# 设置想要自动调参的参数
parameters = { 'n_estimators':[90,100,110],'max_depth': [5,6,7],}
# 初始化模型
clf = xgb.XGBClassifier(seed=42)
f1_scorer = make_scorer(f1_score,pos_label=1)
# 使用 grdi search 自动调参
grid_obj = GridSearchCV(clf,scoring=f1_scorer,param_grid=parameters,cv=5)
grid_obj = grid_obj.fit(X_train,y_train)
# 得到最佳的模型
clf = grid_obj.best_estimator_
# print(clf)
# 查看最终的模型效果
f1, acc = predict_labels(clf, X_train, y_train)
print("F1 score and accuracy score for training set: {:.4f} , {:.4f}。".format(f1 , acc))f1, acc = predict_labels(clf, X_test, y_test)
print("F1 score and accuracy score for test set: {:.4f} , {:.4f}。".format(f1 , acc))

预测时间 in 0.0368 秒
F1 score and accuracy score for training set: 0.7991 , 0.8201。
预测时间 in 0.0149 秒
F1 score and accuracy score for test set: 0.5702 , 0.6133。

4.5 保存模型和加载模型

然后我们可以把模型保存下来，以供以后使用。

import joblib
#保存模型
joblib.dump(clf, 'xgboost_model.model')
#读取模型
xgb = joblib.load('xgboost_model.model')

# 然后我们尝试来进行一个预测
sample1 = X_test.sample(n=5, random_state=2)
y_test_1 = y_test.sample(n=5, random_state=2)
print(sample1)
# 进行预测
y_pred = xgb.predict(sample1)
print("实际值:%s \n预测值:%s"%(y_test_1.values,y_pred))

          HTGD      ATGD  HM1_D  HM1_L  HM1_W  AM1_D  AM1_L  AM1_W  HM2_D  \
70    0.189646 -1.088217      0      0      1      0      1      0      0   
5529 -0.668332 -0.901190      0      1      0      1      0      0      0   
4297 -0.702311 -0.136082      0      1      0      0      1      0      0   
5230 -0.654740 -1.302447      0      0      1      0      1      0      0   
1307  1.438387 -0.269101      1      0      0      0      0      1      0   HM2_L  HM2_W  AM2_D  AM2_L  AM2_W  HM3_D  HM3_L  HM3_W  AM3_D  AM3_L  \
70        0      1      0      1      0      1      0      0      1      0   
5529      0      1      0      1      0      1      0      0      0      1   
4297      1      0      0      1      0      1      0      0      1      0   
5230      1      0      1      0      0      0      1      0      0      1   
1307      0      1      0      0      1      1      0      0      0      0   AM3_W  
70        0  
5529      0  
4297      0  
5230      0  
1307      1  
实际值:[0 0 1 1 1]
预测值:[1 0 1 1 1]

通过以上，我们从 test 数据集中随机挑选5个，预测值跟实际值相同的有 4 个，考虑到我们准确率不高，能够得到这个结果来说还是比较幸运的。

5. 总结与展望：

通过该文章，您应该初步熟悉数据挖掘与分析和机器学习的流程，了解监督学习中逻辑回归模型，支持向量机模型和 XGBoost 模型的基本思想，熟悉机器学习库 Pandas、Scikit-Learn、Searbon、XGBoost、joblib 的基本使用。需要注意的是：如果您未使用 MO 平台，可能还需要安装 XGBoost、SKlearn 等第三方库，目前 Mo 平台已安装常用的机器学习相关的库，可以省去您安装开发平台的时间；另外，数据集也已在平台公开，可以直接导入。目前对于主流的机器学习库的相关资料，我们总结如下：

Python安装
- Anaconnda:下载地址
- IDE:Pycharm下载地址
- Anaconda+Jupyter notebook+Pycharm:安装教程
机器学习工具资料：
- Numpy: 官方文档
- Numpy: 中文文档
- Pandas: 官方文档
- Pandas: 中文文档
- Matplotlib: 官方文档
- Matplotlib: 中文文档
- Scikit-Learn: 官方文档
- Scikit-Learn: 中文文档