今天听完强化课之后去做学习包的题,发现没带平板,如果写到纸上,塞到书里又不知道去哪了,所以索性就拿Latex写了,虽然有一点麻烦,但是好在数量不多,就这么写吧。
都是我自己写的过程,有可能不太正确,大家有什么看法,欢迎在评论区和我一起讨论。
第一题
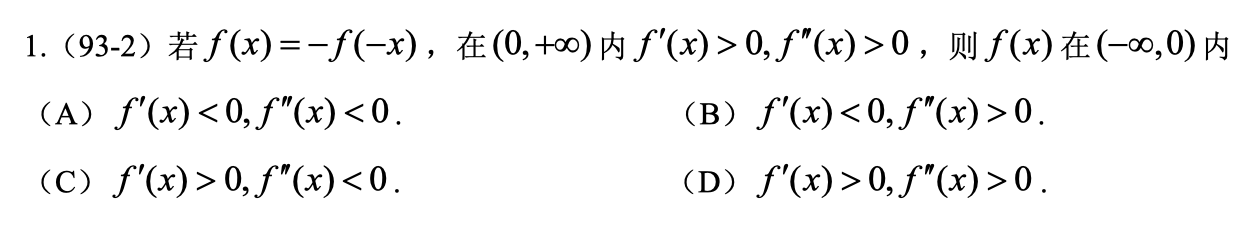
由 f ( x ) = − f ( − x ) 可知, f ( x ) 是奇函数, f ( x ) 可导,所以 f ′ ( x ) 是偶函数, f ′ ′ ( x ) 是奇函数 偶函数根据 y 轴对称,奇函数关于原点对称,根据 f ′ ( x ) > 0 和 f ′ ′ ( x ) > 0 我们可得 f ( x ) 在 ( − ∞ , 0 ) 上 f ′ ( x ) > 0 , f ′ ′ ( x ) < 0 ,选 C 由f(x)=-f(-x)可知,f(x)是奇函数,f(x)可导,所以f{}' (x)是偶函数,f{}'' (x)是奇函数\\ 偶函数根据y轴对称,奇函数关于原点对称,根据f{}' (x)>0和f{}'' (x)>0我们可得\\ f(x)在(-\infty ,0)上f{}' (x)>0,f{}'' (x)<0,选C 由f(x)=−f(−x)可知,f(x)是奇函数,f(x)可导,所以f′(x)是偶函数,f′′(x)是奇函数偶函数根据y轴对称,奇函数关于原点对称,根据f′(x)>0和f′′(x)>0我们可得f(x)在(−∞,0)上f′(x)>0,f′′(x)<0,选C
第二题

A B :反例 f ( x ) = x 3 单调递增,但是 f ′ ( x ) ≥ 0 C : 反例 f ( x ) = x AB:反例f(x)=x^3单调递增,但是f{}' (x)\ge 0 \\ C:反例f(x)=x AB:反例f(x)=x3单调递增,但是f′(x)≥0C:反例f(x)=x
第三题

由题意得,函数 f ( x ) 是偶函数,则 f ′ ( x ) 是奇函数, f ′ ′ ( x ) 是偶函数 和第一题类似, f ′ ( x ) 在 ( 0 , ∞ ) < 0 , f ′ ′ ( x ) 在 ( 0 , ∞ ) < 0 , 选 C 由题意得,函数f(x)是偶函数,则f{}'(x)是奇函数,f{}''(x)是偶函数\\ 和第一题类似,f{}'(x)在(0,\infty )<0,f{}''(x)在(0,\infty )<0,选C 由题意得,函数f(x)是偶函数,则f′(x)是奇函数,f′′(x)是偶函数和第一题类似,f′(x)在(0,∞)<0,f′′(x)在(0,∞)<0,选C
第四题

根据选项,我们挨个判断:若 lim x → − 1 + f ( x ) = − s i n 3 18 , 若 lim x → 0 − f ( x ) = − s i n 2 4 题目真友好,第一个选项就是对的,选 A 根据选项,我们挨个判断:若\lim_{x \to -1^+} f(x)=\frac{-sin3}{18}, 若\lim_{x \to 0^-} f(x)=-\frac{sin2}{4}\\ 题目真友好,第一个选项就是对的,选A 根据选项,我们挨个判断:若x→−1+limf(x)=18−sin3,若x→0−limf(x)=−4sin2题目真友好,第一个选项就是对的,选A
第五题

由题意得, f ( x ) 连续, f ′ ( 0 ) > 0 , 将 f ′ ( 0 ) 写成极限形式就是 lim x → 0 f ( x ) − f ( 0 ) x − 0 > 0 ,根据极限的保号性,我们可以使用脱帽法 所以 f ( x ) − f ( 0 ) x − 0 > 0 ,找到 A B 的反例,就是 f ( x ) = { x + 2 x 2 s i n 1 x , x ≠ 0 0 , x = 0 这一函数在 0 的导数大于 0 ,但是其去心邻域都小于 0 ,选 C 由题意得,f(x)连续,f{}'(0)>0,将f{}'(0)写成极限形式就是\\ \lim_{x \to 0} \frac{f(x)-f(0)}{x-0} >0,根据极限的保号性,我们可以使用脱帽法\\ 所以 \frac{f(x)-f(0)}{x-0} >0,找到AB的反例,就是f(x)=\left\{\begin{matrix}x+2x^2sin\frac{1}{x} ,x\ne 0 & \\ 0 , x=0& \end{matrix}\right. \\ 这一函数在0的导数大于0,但是其去心邻域都小于0,选C 由题意得,f(x)连续,f′(0)>0,将f′(0)写成极限形式就是x→0limx−0f(x)−f(0)>0,根据极限的保号性,我们可以使用脱帽法所以x−0f(x)−f(0)>0,找到AB的反例,就是f(x)={x+2x2sinx1,x=00,x=0这一函数在0的导数大于0,但是其去心邻域都小于0,选C
第六题
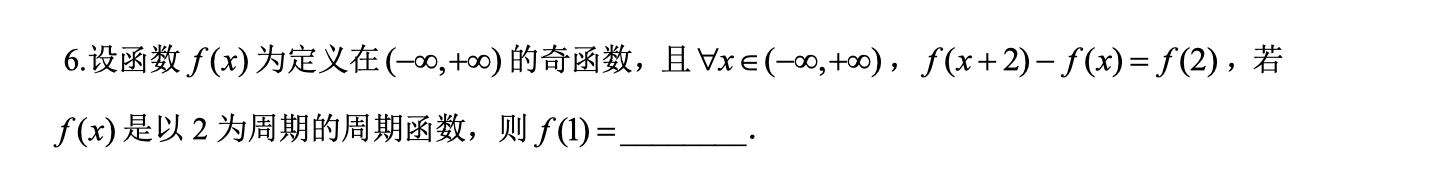
感觉第一眼看上去是个高中题, f ( x + 2 ) − f ( x ) = f ( 2 ) , 带入 x = 1 , f ( 3 ) − ( 1 ) = f ( 2 ) , 带入 x = − 1 , f ( 1 ) − f ( − 1 ) = f ( 2 ) ,又 f ( − 1 ) = − f ( 1 ) , 所以 f ( 1 ) = 0 感觉第一眼看上去是个高中题,f(x+2)-f(x)=f(2),带入x=1,f(3)-(1)=f(2),带入x=-1,f(1)-f(-1)=f(2),又f(-1)=-f(1),所以f(1)=0 感觉第一眼看上去是个高中题,f(x+2)−f(x)=f(2),带入x=1,f(3)−(1)=f(2),带入x=−1,f(1)−f(−1)=f(2),又f(−1)=−f(1),所以f(1)=0
函数章节思维导图
因为上课没带讲义,我就用的思维导图,看起来还挺方便的
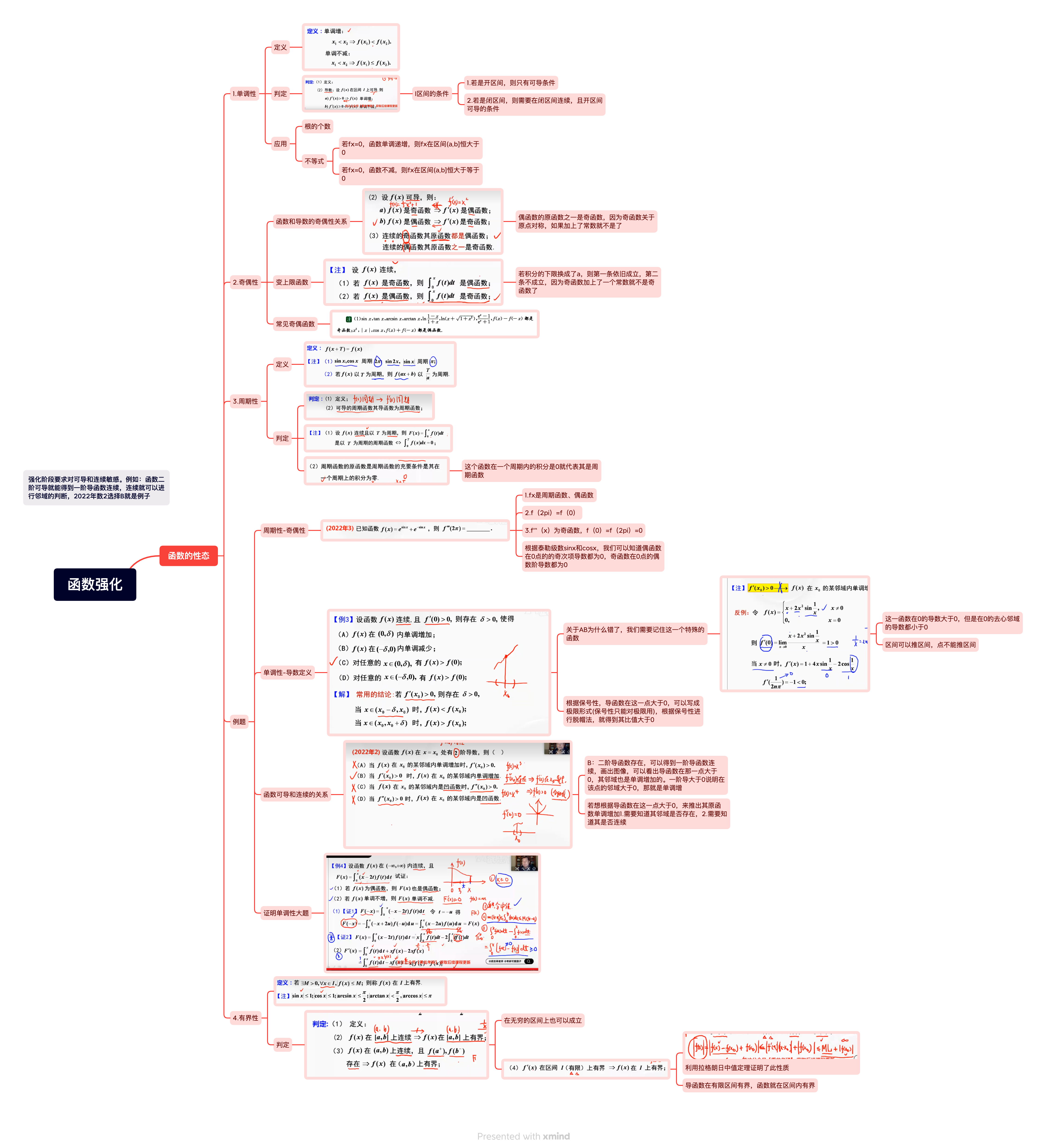
需要pdf的看这里:函数强化
提取码: xgsv