一、区间估计与假设检验的联系与区别

• 联系：二者利用样本进行推断，都属于推断统计
• 区别：
  1. 原理： 前者是基于大概率，后者基于小概率；
  2. 统计量：前者是构造枢轴量（不含未知参数，分布明确），后者是检验统计量；
  3. 结果：前者是区间，后者是对假设作出判断；

二、原假设和备择假设的选取

• 原假设是不会轻易否定、传统的、已有的、大众所认为的、被保护的
• 原假设是我们想要拒绝的，备择假设是我们想要接受的假设

三、极大释然估计的基本思想和计算流程

• ⭐️ 基本思想：在已知总体的概率分布时，反推最有可能（最大概率）使得样本结果出现的模型参数值；（出现认为最有可能发生的）
• 计算流程：
  1. 构造极大似然函数
  2. 取对数
  3. 对未知参数求导并令导数等于0
  4. 反解出未知参数

四、概率和统计的区别

• 概率：已知模型和参数----->计算数量特征（均值、方差等）
• 统计：已知样本数据-------->估计模型和参数

五、什么是随机变量？

“随机变量”我们一般讨论的是离散型随机变量和连续型随机变量，，其引入的目的是将试验结果目的化。随机变量的本质是一个映射函数。

六、大数定理和中心极限定理（⭐️⭐️⭐️）

• 大数定理：就是样本均值收敛到总体均值（侧重期望本身）
  1. 弱大数定理（辛钦大数定理）：样本均值依概率收敛于期望值
  2. 强大数定理：样本均值依概率1收敛于期望值
• 中心极限定理：当样本量足够大时，样本均值的分布慢慢变成正态分布（侧重期望分布）

七、大数定理和中心极限定理的应用

• 大数定理的应用：在没有得到总体全部数据的情况下，可以用样本估计总体（中心极限定理也有这个作用）抛硬币，抛得次数足够得多，正反面出现的概率几乎一致
• 中心极限定理的应用：在统计推断中，常需要知道统计量的分布，例如假设检验。这时可以借助大样本理论，在样本量很大时，求出统计量的渐进分布

八、为什么特征函数可以唯一确定分布函数？（不确定）

将特征函数展开，其展开式中包含有各阶原点矩

九、依分布收敛、依概率收敛、几乎处处收敛

几乎处处收敛----->依概率收敛------>依分布收敛

• 依分布收敛：只需要考虑每个随机序列的累积效应，也就是分布函数，而不关注每个x的取值，它是一种点点收敛；
• 依概率收敛：不仅蕴含随机序列的累积效应，也蕴含了每个序列具体取值情形，所以依概率收敛更强；

十、极大释然估计有偏的例子

经典例子：正态分布中的方差的估计（就是分母为n的那一个，一般用的n-1那个作为无偏估计量）

十一、什么是充分统计量？⭐️

简单的说，知道了充分统计量我们就可以扔掉样本，因为样本里的信息全都被包含在充分统计量里面。例如，收集了500条数据，然后你计算了这批数据的均值和方差，然后你出去吃了午饭回来发现数据丢失了，但这时候没关系，因为所计算的均值和方差已经包含了这批数据的全部信息。
（ps.完备统计量就是基于对总体参数的无偏估计量至多一个；次序统计量就是将Xn按照顺序排列后得到的统计量，其具体形式一般为X1,X2,X3…Xn）

十二、估计的性质

• 大样本性质
  相合性（一致性）、渐进正态性（估计分布收敛于正太分布）

• 小样本性质
  无偏性

十三、P值？a值？⭐️

• P值：原假设成立时，样本观测结果或更为极端结果所出现的概率，是观测得到显著性水平。它度量了样本所提供地证据对原假设的支持程度，p值越小，我们拒绝的理由越充分。p<a则拒绝原假设；
• a值：假设检验中犯第一类错误的上限值；

十四、假设检验的原理及步骤

• ⭐️ 假设检验原理：小概率原理（小概率事件在一次试验中几乎不会发生，当发生了，我们就有理由认为之前的假设有为问题，这里的小概率就是显著性水平的值，一般取0.05或者0.01，有点反证的感觉）
• 假设检验的步骤：
  1. 提出假设
  2. 抽取样本
  3. 确定检验统计量和统计量的分布
  4. 根据显著性水平确定拒绝域
  5. 作出决策

十五、总体、样本、参数、统计量、变量、抽样分布

总体：包含所研究的全部个体的集合
样本：从总体中抽取一部分形成的总体的一个子集
参数：说明总体特征的概括型数字度量
统计量：不含有任何未知参数的样本函数，是样本特征的概括型数字度量
变量：说明现象某种特征的概念
抽样分布：样本统计量的概率分布

十六、概率的三条共理

• 任何事件概率大于0，PA>=0
• 样本空间发生的可能性大于1
• 可列可加性（要求事件之间互斥）

十七、矩估计和极大释然估计的优缺点

• 矩估计
  1. 优点：事先不需要知道总体的分布，计算简单，在大样本下精度高
  2. 缺点：小样本下估计的精度低，不唯一
• 极大释然估计
  1. 优点：估计结果更显著，更有效，估计偏差更小，精度高
  2. 缺点：需要事先知道总体的分布

十八、假设检验涉及的两类错误？为什么要首先控制犯第一类错误的概率？

• 第一类错误：原假设为真时我们拒绝原假设所犯的错误，也称为弃真错误，其犯错误的概率通常记作a
• 第二类错误：原假设为伪时我们没有拒绝原假设，也称作纳伪错误，其犯错误的概率通常记作β
• 控制犯第一类错误的原因：
  1. 统一原则
  2. 原假设往往是确定的，而备择假设往往是模糊的；

十九、概率空间及三要素

• 概率空间：总测度为1的测度空间，（Ω,F,P）
  Ω：样本空间
  F：事件的集合，他是样本空间中一些元素构成的子集
  P：概率（3中解释）

二十、期望和方差

二者计算式子

• 期望：数据集中趋势的主要度量
• 方差：数据离散程度的主要度量（这里注意区分样本方差和总体方差的差别）

二十一、置信度(水平)、置信区间

• 置信度：重复多次试验构造置信区间，包含总体参数真值的置信区间个数占总个数的比例。（这里可以用撒渔网来解释）；
• 置信区间：由样本统计量构造的包含或不包含总体参数区间真值的区间（注意这里千万不能说以多大概率包含）

二十二、概率为0的事件是否必然不会发生？或者说概率为1的事件是否一定发生？

二者都是否定的。这一定要联系连续情况中的实际的例子。前者可以用均匀分布中一点来说明。而后者主要是用开区间来说明，落在（0,1）的概率为1，但是取到0却不会发生；

二十三、概率和频率的关系

在概率的数理统计定义中，随着n的增大，逐渐稳定的频率就是概率。概率更多见于概率论中，是一个理想值；频率更多得见于统计中，是一个实验值。

二十四、假设检验统计量

• 在样本均值的假设检验中主要注意一点，在大样本情况下，z和t是可以互换，而在小样本以及总体方差未知时，此时因为总体均值分布会有偏，此时只能用t，否则误差过大；
• 在总体方差的假设检验中，主要是使用卡方统计量；
• 方差比的检验主要是使用F统计量；
  这一部分复试前看一哈书中的表即可

二十五、说明统计量好坏的三个标准

• 无偏性：指统计量的期望等于被估计的总体的参数值；（如样本均值）
• 有效性：针对同一无偏估计量，方差越小的越有效；（如样本方差，自由度为n-1的原因）
• 一致性：随着样本量n的逐渐增大，统计量的值越来越接近被估计的总体参数；（如样本均值）

二十六、贝叶斯估计和传统估计的区别

ps.只需回答前2点

• 参数的解释不同：
  传统：待估参数是确定
  bayes：待估参数是服从某种分布的随机变量
• 利用的信息不同：
  传统：只利用样本信息
  bayes：要求事先提供一个参数的先验分布
• 随机误差项的要求不同：
  传统：不要求知道随机误差项的具体分布形式（除最大释然估计）
  bayes：要知道随机误差项的具体分布形式
• 选择参数估计量的准则不同
  传统：以ols最大似然为准则求解参数估计量
  bayes：构造一个损失函数并以损失函数最小化为准则求得参数估计量.

二十七、点估计和区间估计的区别

二者都属于参数估计

• 点估计：常用的点估计包括矩估计、最大释然估计、最小二乘估计，他所得到的结果就是一个具体值（这里注意参数估计方法的举例）；
• 区间估计：最后的结果是在点估计的基础上，给出一个包含或者不含总体参数真值的一个区间
  当然这里也可以从评判估计的标准来说，点估计主要是用无偏性、有效性、一致性来评估好坏，而区间估计主要是由置信度和精确度评价的；

二十八、独立与相关性的关系⭐️

先分别解释两个词语：
独立：指两变量不包含任何关系，包括线性关系和非线性关系
相关关系：反映两个变量之间的线性关系
二者关系：在二维正态中，不相关与独立等价，即独立一定不相关，相关一定不独立；而其它情况中，相关一定不独立，而独立不一定不相关；
ps.独立是没有传递性的，另外这里也要知道三个变量独立性中的两两独立和三者相互独立的区别

二十九、矩估计的理论依据是什么？

其理论依据为格里汶科定理：即当n充分大时，样本分布函数近似地等于总体分布函数

三十、相关系数？协方差？

二者的计算式

• 相关系数：度量两个变量之间的线性相关性程度的统计量
• 协方差：衡量两个变量的总体误差

三十一、势函数

样本观测值落在拒绝域内的概率

三十二、为什么要我们避免“接受H0”这样的说法？⭐️⭐️

在这里以法庭审判一个例子来解释，在法庭审判中，我们往往当我们没有搜集到足够的证据，此时我们只能说，在这个证据下面无法说明被告有罪，但同时也没有证据说明他清白。在假设检验道理相同，我们在做推翻原假设的小概率事件，如果小概率没有发生，此时只能说明我没有找到拒绝H0的原因，但此时也没有能够说明H0是正确的事件发生

三十三、细说三大分布？以及t分布和F分布的关系？⭐️

• 卡方分布：独立同分布的标准正态分布的平方和
• t分布
• F分布
  随着n的逐渐增大，t分布以F分布为渐近分布

这里只强调几点，首先要求各变量独立

三十四、那些分布有无记忆性？什么是无记忆性？⭐️

离散型：几何分布
连续型：指数分布
无记忆性：用零件的那个例子来回答

三十五、切比雪夫不等式⭐️

某个事件与均值的偏离值的概率与方差和该概率值有关

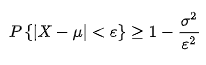
三十六、蒙特卡洛方法

是随机抽样技术，是一种模拟实验

• 随机投点法
• 平均值法

三十七、简述EM算法（缺失数据的估计）

• 根据观测数据，估计（最大释然估计）出模型参数的值；
• 根据估计出的参数值估计缺失值
• 估计出的缺失值加上之前的观测数据重新对模型的参数值进行估计
  反复迭代以上，直到收敛，迭代结束。

三十八、非参数检验方法

柯-斯检验法，卡方优度拟合检验、游程检验、符号检验

三十九、正态性检验方法

• w检验（适用小样本）
• D检验（适用大样本）
• WCM检验
• 峰度检验

四十、常见的降维方法？并详细介绍一下主成分分析？

逐步回归、SIS、LASSO、PCA，ICA、随机森林等
主成分分析：是一种常用的降低维度的方法（结合项目实际来谈），基本原理就是投影

应用统计432考研复试提问总结精简版【二】

最近发现有很多小伙伴在看这篇文章，看到这里，我想你们最近压力应该挺大。在这里，我有一些话分享给你们：现在大多数人都在思考如果没考上怎么办？无论你是选择二战还是工作我觉得都是没有问题的，尤其是针对工作的问题，大家都有点“脱不下长衫”。其实，不要有负担，不要成为他们，做你自己最想做的。哪怕是回家种橘子，你也要用你的知识去让你橘子品质足够好，好到能够成为中国标准，能够出口国外；哪怕是你去餐厅洗碗，你也要建立所有的流程化体系，让其成为行业标准。在当下中国这个时代，我们都被“身份”控制得死死的，大多数人都告诉我们，没有这样的或那样的身份你就做不了什么，人们把这个时代渲染得过分压抑，好像没了这个身份，人生就有遗憾。其实真正遗憾是不能够有足够时间去陪伴家人，没有机会出去旅游，没有学会开车，没能够学会游泳…这些遗憾会在你人生某个时刻让你难受至极，而所谓身份遗憾，你只会感叹到不过如此。