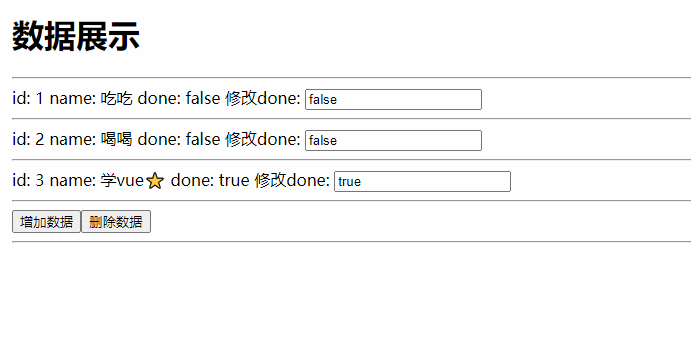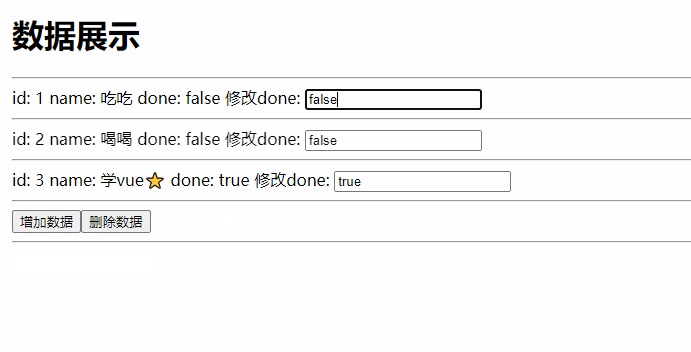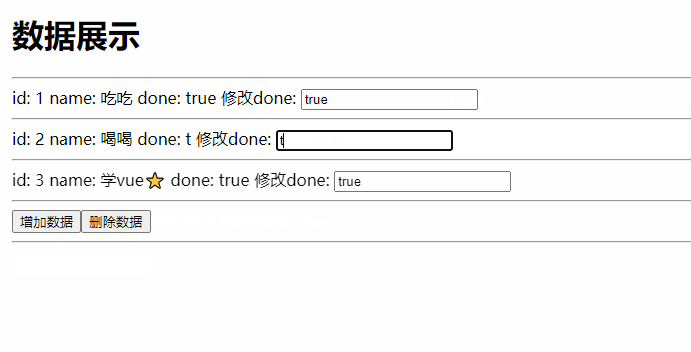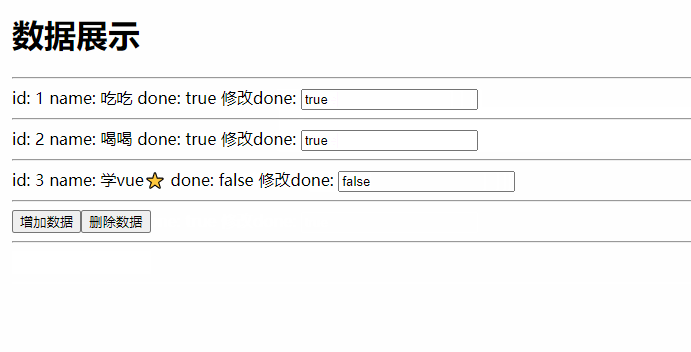
给你一棵二叉树的根节点 root ，请你构造一个下标从 0 开始、大小为 m x n 的字符串矩阵 res ，用以表示树的 格式化布局 。构造此格式化布局矩阵需要遵循以下规则：

树的 高度 为 height ，矩阵的行数 m 应该等于 height + 1 。
矩阵的列数 n 应该等于 2height+1 - 1 。
根节点 需要放置在 顶行 的 正中间 ，对应位置为 res[0][(n-1)/2] 。
对于放置在矩阵中的每个节点，设对应位置为 res[r][c] ，将其左子节点放置在 res[r+1][c-2height-r-1] ，右子节点放置在 res[r+1][c+2height-r-1] 。
继续这一过程，直到树中的所有节点都妥善放置。
任意空单元格都应该包含空字符串 “” 。
返回构造得到的矩阵 res 。

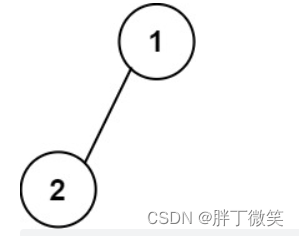
输入：root = [1,2]
输出：
二叉树高度为1
所以矩阵的行数为1+1=2；
列数为2^(1+1)-1=3
[["","1",""],  ["2","",""]]

解：

public List<List<String>> printTree(TreeNode root) {//获取高度int height = getHeight(root);String[][] ans = new String[height][(1 << height) - 1];for (String[] arr : ans) {Arrays.fill(arr, "");}List<List<String>> res = new ArrayList<>();fill(ans, root, 0, 0, ans[0].length);for (String[] arr : ans) {res.add(Arrays.asList(arr));}return res;}/*** 填充数组*ans  数组*root 根节点*i    第几行*l    左节点*r    右节点*/private void fill(String[][] ans, TreeNode root, int i, int l, int r) {if (root == null) {return;}ans[i][(l + r) / 2] = "" + root.val;fill(ans, root.left, i + 1, l, (l + r) / 2);fill(ans, root.right, i + 1, (l + r + 1) / 2, r);}//获取树的高度private int getHeight(TreeNode root) {if (root == null) {return 0;}return Math.max(getHeight(root.left), getHeight(root.right)) + 1;}

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/print-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。