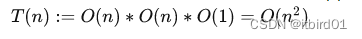趣学算法第二次

14天阅读挑战赛
一、一棋盘的麦子

计算一棋盘的麦子，python代码如下：

import matplotlib.pyplot as plt
s=[]
def cal(n):sum=0i=0while i<=n:sum=sum+pow(2,i)i+=1s.append(sum)return s
n=int(input("请输入一个数："))
x=range(n+1)
for j in x:cal(j)
plt.plot(x,s)
plt.show()

可视化如下：

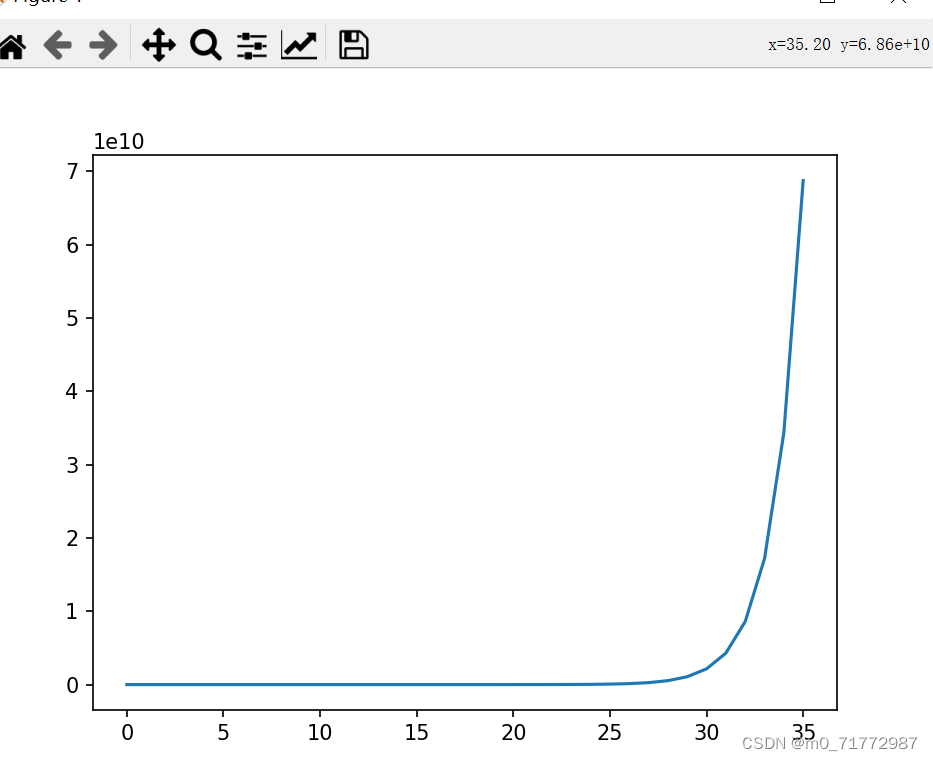
此时n输入的值为35，此时已达到了10次方，且曲线快速增长，让我们见识到了指数的力量，所以全国的麦子也放不满棋盘也就不足为奇啦。

算法时间复杂度排序从低到高如下：

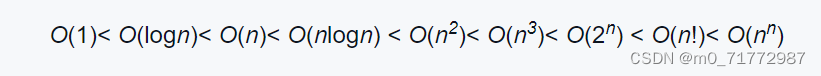
二、神奇的兔子序列（斐波那契数列）

表达式如下：

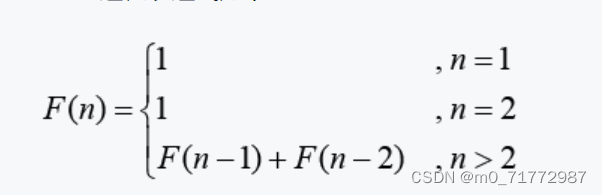
斐波那契数列的规律：从第三项起，每一项的值=前两项之和

python代码实现如下：

def Fabonacci(n):if n==1 or n==2:return 1if n>=3:return Fabonacci(n-1)+Fabonacci(n-2)
n=int(input("请输入一个数:"))
print(Fabonacci(n))

但上面这个实际上是一个指数级算法，当想知道第40项以上的数时，程序运行就有点慢了，所以我们要对算法进行优化，降低算法的复杂度；

def Fabonacci(n):if n==1 or n==2:return 1i=3tem=0s1 = 1s2 = 1while i<=n:tem=s1+s2s1=s2s2=temi+=1return tem
n=int(input("请输入一个数:"))
print(Fabonacci(n))

此时时间复杂度为O(n)，从指数级降到了线性

三、数学之美：斐波那契数列的项数n趋近于无穷大时，前一项与后一项的比值越来越接近黄金数列，代码如下：

import matplotlib.pyplot as plt
bilv=[]
def Fabonacci(n):if n==1 or n==2:return 1i=3tem=0s1 = 1s2 = 1while i<=n:tem=s1+s2s1=s2s2=temi+=1return tem
n=int(input("请输入一个数："))for i in range(3,n):a=Fabonacci(i-1)/Fabonacci(i)bilv.append(a)
plt.plot(range(len(bilv)),bilv)
plt.show()