小偷偷东西问题

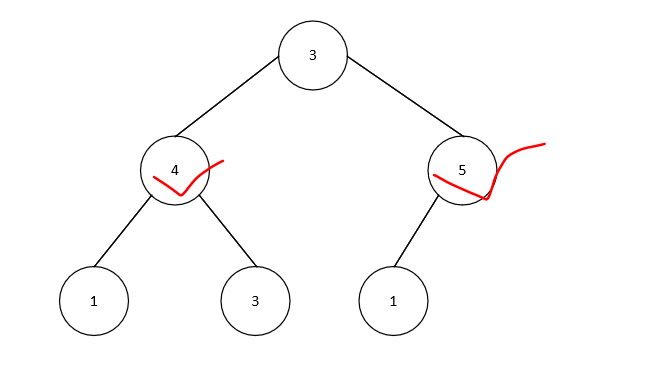
• 前言
  • 深度优先遍历是经典的图论算法，深度优先遍历算法的搜索逻辑和它的名字一样，只要有可能，就尽量深入搜索，直到找到答案，或者尝试了所有可能后确定没有解。
  • 简单来说，深度优先遍历就是按照某规则（如检索当前节点的第一个子节点）检索某个节点，直到检索完毕再去检索其他节点。
  • 搜索问题的本质就是试探问题的所有可能选择，按照特定的规律和顺序，不断去搜索答案，直到找到问题的解。如果把所有可能都走了一遍，还没有找到解，就说明这个问题没有解。注意：深度优先遍历一定要按照规则尝试所有的可能。
  • 深度优先遍历是图论的经典算法，从某个节点v出发开始进行搜索，不断搜索直到该节点的所有边都被遍历完。当节点v的所有边都被遍历以后，深度优先遍历算法则需要回溯到v的前驱节点，来继续搜索这个前驱节点的其他边。如果还存在尚未被遍历的节点，则深度优先遍历算法会按照统一的规则从这些剩下的节点中选择一个节点再重复同样的遍历过程。这样的搜索过程从最开始的节点一直持续到最后一个节点的所有边都遍历完。
  • 二叉树的先序、后序和中序都属于深度优先遍历，层序遍历属于广度优先遍历。（关于二叉树的数据结构只是不提）
• 问题描述
  • 有一个小区的别墅按照二叉树结构分布，也就是说，除了第一个别墅，其余每个别墅都和另一个“父”别墅连接。现在有个小偷，想要进入别墅偷窃，但是，一旦进入两个直接连接的别墅（只会有一段线相连），警报会触发，每个节点的值表示别墅财务的价值，问如何走在不报警的情况下偷得最多财物。
  • 
• 问题分析
  • 对于上图，显然我选择头4和5这两个别墅，得到最多财物。
  • 显然，一旦选择了某个节点，就意味着放弃所有的这个节点的直接子节点（在下一层与之相连的节点）。
  • 不妨定义节点这个数据结构记录当前节点的价值，以及偷了该节点得到的价值和不偷该节点得到的价值。很容易发现，每个节点的偷值是左侧子节点的不偷值+右侧子节点的不偷值+节点的价值，每个节点的不偷值是左侧子节点的最大值（偷与不偷中较大者）+右侧子节点的最大值。
  • 那么想要得到根节点的偷与不偷值，只要知道其子节点的，其子节点的又是来自子节点的子节点的，显然，这是一个递归过程，最底层节点的属性值一开始是确定的，用来构造父节点的属性值。最后输出根节点的两值较大者即可。
• 代码

  •   # -*-coding:utf-8-*-class TreeNode:def __init__(self, x, l, r):self.value = xself.left = lself.right = rdef get_value(root):rst = search(root)return max(rst[0], rst[1])def search(root):"""返回二维数组[偷值，不偷值]:param root::return:"""if root is None:return [0, 0]left = search(root.left)right = search(root.right)rob_value = root.value + left[1] + right[1]skip_value = max(left[0], left[1]) + max(right[0], right[1])return rob_value, skip_valueif __name__ == '__main__':f = TreeNode(1, None, None)e = TreeNode(3, None, None)d = TreeNode(1, None, None)b = TreeNode(4, d, e)c = TreeNode(5, f, None)a = TreeNode(3, b, c)print(get_value(a))

• 补充说明
  • 具体代码可以查看我的Github，欢迎Star或者Fork
  • 参考书《你也能看得懂的Python算法书》
  • 显然，这种思路适合求得最优解，但是对于输出具体路径略显麻烦。