💓博主CSDN主页:杭电码农-NEO💓
 
⏩专栏分类:八大排序专栏⏪
 
🚚代码仓库:NEO的学习日记🚚
 
🌹关注我🫵带你学习排序知识
  🔝🔝

---

1. 前言🚩

插入排序一般来说是低效的
因为它一次只能挪动一个数据
如果你不知道插入排序可跳转插入排序

所以Donald Shell(希尔)这个人
对插入排序进行了优化
将插入排序提升了不止一个档次
甚至可以和快速排序平起平坐!

希尔不仅天资聪慧,并且很长寿
它足足活了91岁!
放在整个天才届也是相当炸裂的存在
(天才数学家阿贝尔已经哭晕在厕所)
阿贝尔简介

---

2. 希尔排序思路🚩

基本思路:

• 在直接插入排序上做优化:
  1. 分组预排序,使数组接近有序
2. 直接插入排序

为什么要这样做?

我们在将插入排序的时候提到:
对于有序的数组
插入排序的时间复杂度为O(N).
 
所以这里我们先预排序
让数组接近有序再去直接插入排序
这样效率会大大提升!

插入排序讲解链接点击即可访问

---

3. 预排序思路讲解🚩

希尔是这样想的:

将一个数组按gap分组.
再将分组的值进行插入排序

比如:我们定义一个0~9的无序数组:

int a[10]={9,1,2,5,7,4,8,6,3,5};

假设这里的gap等于3:

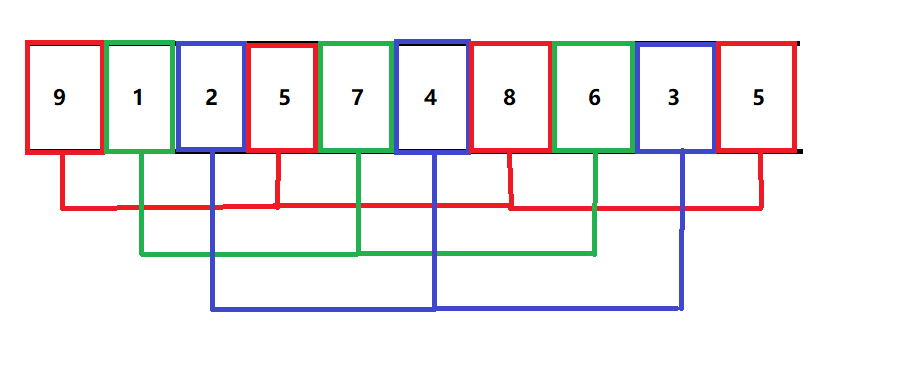
这里,9.5.8.5分为一组
1.7.6 分为一组
2.4.3 分为一组

再将数据: 9.5.8.5进行插入排序
1.7.6进行插入排序
2.4.3进行插入排序

排完后变成了这样:

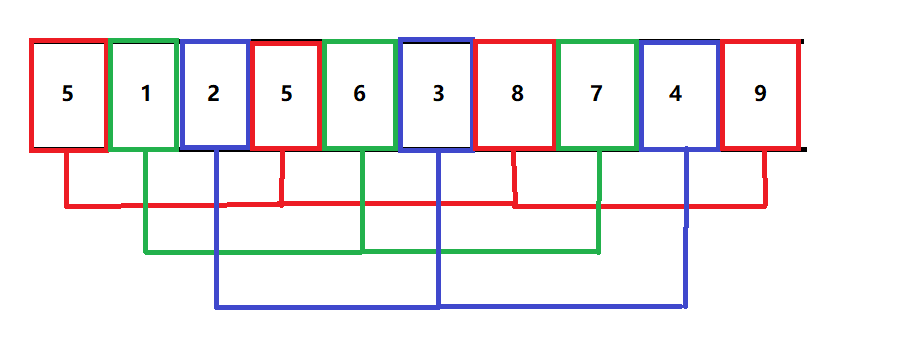
单独看红色一组:5.5.8.9.是有序的
单独看绿色一组:1.6.7.也是有序的
单独看蓝色一组:2.3.4.也是有序的
数组整体比刚才有序了,目的达到!

---

4. 预排序代码实现🚩

当gap等于3时,我们要排三个颜色的组
当gap等于4时,就要排四个颜色的组
我们从内到外,先写排一组数据的代码

for (int i = 0; i < n - gap; i+=gap)//end最多走到n-gap位置{                              //这个数组中end最多到8,这时x=5为最后一个元素int end = i;int x = a[end + gap];//插入排序中gap等于1,就是加一while (end >= 0){if (a[end] > x){a[end + gap] = a[end];end =end-gap;}else{break;}}a[end + gap] = x;}

我们细心观察可以发现:
这里的分组预排和插入的思路是一样的

只不过插入排序的gap等于1而已!

我们可以看看插入排序:

---

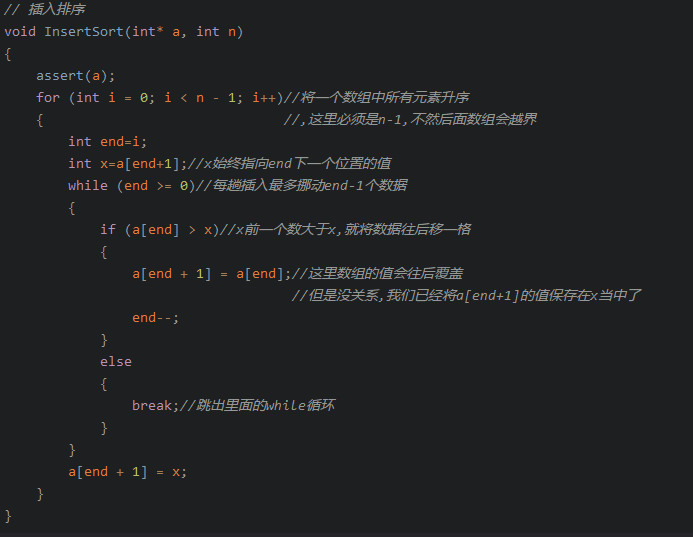
5. 对于gap取值的思考🚩

gap的取值方法有很多种.
但是每一种gap的取值都满足:
先大后小原则
也就是我们的预排序不止排序一次
gap会由大变小,常见的取值有:

gap=n/2 (n为数组长度)
gap=n/3 (n为数组长度)

比方说用gap=n/2做例子.
当数组长度为100时.我们需要进行:
gap=50.gap=25.gap=12.
gap=6.gap=3.这么多次预排序
直到gap=1,停止预排,进行直接插入

---

用刚才定义的数组可以得到这样的图:

---

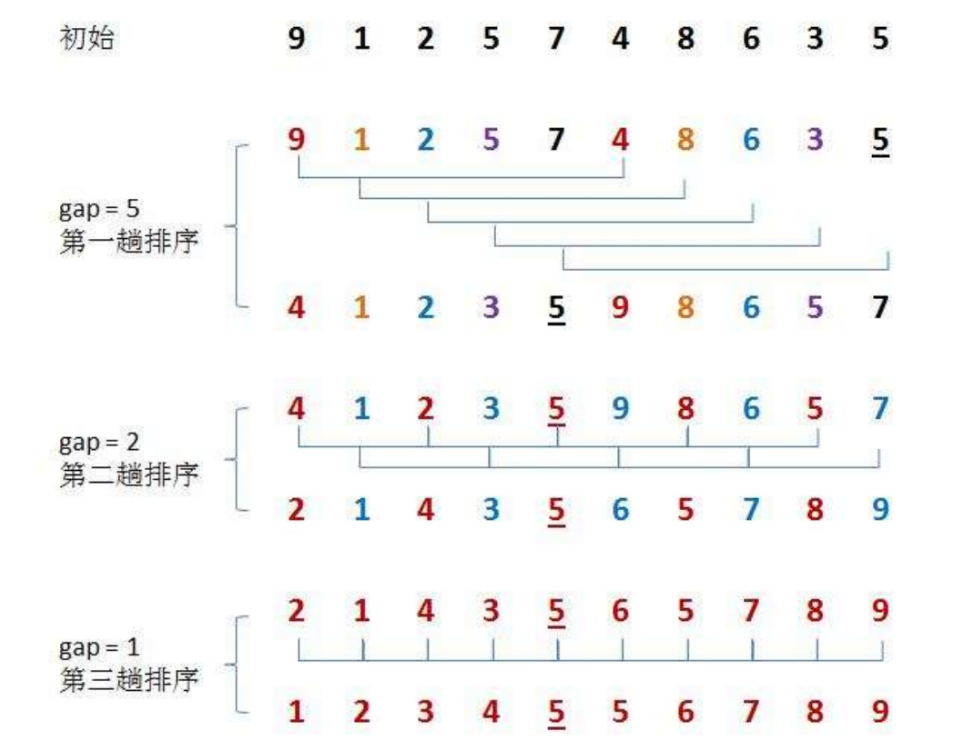
6. 完整的希尔排序🚩

有了前面关于,一组数据的插入排序
和对于gap取值的理解后,展现所有代码

// 希尔排序
void ShellSort(int* a, int n)
{//多次预排序加直接插入排序int gap = n;while (gap > 1){gap = gap / 2;//gap = gap / 3 + 1;也可以是gap/3// 多组一锅炖for (int i = 0; i < n - gap; ++i){int end = i;int x = a[end + gap];while (end >= 0){if (a[end] > x){a[end + gap] = a[end];end =end-gap;}else{break;}}a[end + gap] = x;}}
}

对于代码的解释:

1. 对于gap的解释

• gap=gap/3时要加上1
• 因为gap/3后的值可能跳过1直接为零

2. 多组数据一锅炖的理解

• 这里其实有两种写法来实现gap组预排:

第一种:

for(int j=0;j<gap;j++)
{for (int i = j; i < n - gap; i+=gap){...}
}

这种是先排完红色的一组,再排其他颜色

第二种:

for (int i = 0; i < n - gap; ++i)
{...
}

这种是:
先排红色中的9,再排绿色的1.按照顺序走

• 不管用哪种方法,效率都是一样的

---

7. 希尔排序算法效率分析🚩

希尔排序的时间复杂度不好算
因为gap取值方法千变万化
并且每次预排后的直接插入不好估定

一般默认希尔排序的时间复杂度为:

O ( N * log₂ N) 或
O (N * log₃ N)

---

但是这里我还是翻阅了一些资料
我发现在严蔚敏先生写的
《数据结构C语言版》
 
和殷人昆先生写的
《数据结构-用面相对象方法与C++描述》
中给出了一些数据研究:

根据大量实验得出的数据:
时间复杂度范围:

n^1.25 ~ 1.6n^1.25
也可以直接看作: n^1.3

不管是哪个取值
对于插入排序的优化都很明显了!

---

8. 总结🚩

希尔排序是一个效率非常不错的排序
它与快速排序,堆排序,归并排序
合称"排序四大天王"(我自己定的).
在未来的笔试,面试中会经常遇见它们

---

🔎 下期预告:堆排序 🔍