Day53

最长公共子序列

1143. 最长公共子序列 - 力扣（LeetCode）

题目

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。

若这两个字符串没有公共子序列，则返回 0。

示例 1:

• 输入：text1 = “abcde”, text2 = “ace”
• 输出：3
• 解释：最长公共子序列是 “ace”，它的长度为 3。

示例 2:

• 输入：text1 = “abc”, text2 = “abc”
• 输出：3
• 解释：最长公共子序列是 “abc”，它的长度为 3。

示例 3:

• 输入：text1 = “abc”, text2 = “def”
• 输出：0
• 解释：两个字符串没有公共子序列，返回 0。

提示:

• 1 <= text1.length <= 1000
• 1 <= text2.length <= 1000 输入的字符串只含有小写英文字符。

思路

动规五部曲

• 确定dp数组以及下标的含义

dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]

• 确定递推公式

主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同

如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;

如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。

即：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);

if (text1[i - 1] == text2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;
} else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}

• dp数组如何初始化

先看看dp[i][0]应该是多少呢？

test1[0, i-1]和空串的最长公共子序列自然是0，所以dp[i][0] = 0;

同理dp[0][j]也是0。

其他下标都是随着递推公式逐步覆盖，初始为多少都可以，那么就统一初始为0。

• 确定遍历顺序

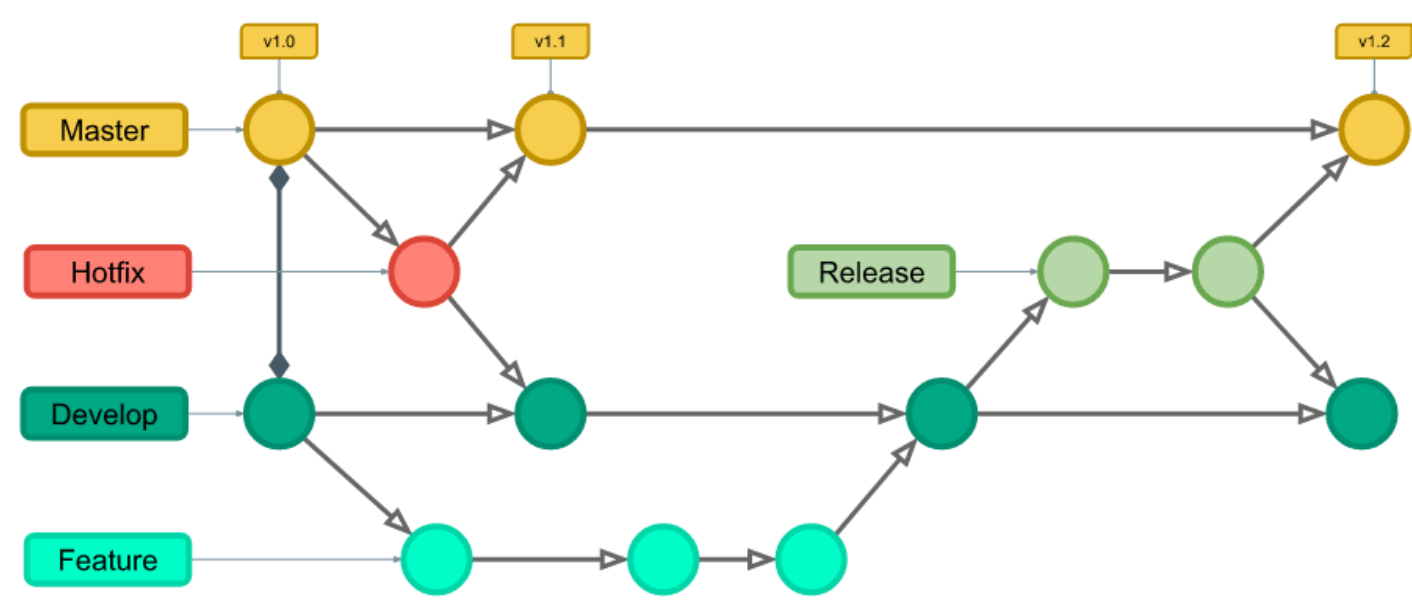
从递推公式，可以看出，有三个方向可以推出dp[i][j]，如图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-j9lf6ObI-1691065715519)(https://code-thinking-1253855093.file.myqcloud.com/pics/20210204115139616.jpg “1143.最长公共子序列”)]

那么为了在递推的过程中，这三个方向都是经过计算的数值，所以要从前向后，从上到下来遍历这个矩阵。

• 举例推导公式

以输入：text1 = “abcde”, text2 = “ace” 为例，dp状态如图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-C57VOQAx-1691065715520)(https://code-thinking-1253855093.file.myqcloud.com/pics/20210210150215918.jpg “1143.最长公共子序列1”)]

最后红框dp[text1.size()][text2.size()]为最终结果

代码

class Solution {public int longestCommonSubsequence(String text1, String text2) {int len1 = text1.length();int len2 = text2.length();// dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]int dp[][] = new int[len1 + 1][len2 + 1];// 长度为[0, i - 1]的字符串text1 在 i = 0 时 text1是空字符串，初始化 dp[0][j] = 0， text2同理 dp[i][0] = 0// dp[0][0] = 0;for(int i = 1; i < len1 + 1; i++){char t1 = text1.charAt(i - 1);for(int j = 1; j < len2 + 1; j++){if(t1 == text2.charAt(j - 1)){dp[i][j] = dp[i - 1][j - 1] + 1;}else{dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[len1][len2];}
}

不相交的线

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

题目

我们在两条独立的水平线上按给定的顺序写下 A 和 B 中的整数。

现在，我们可以绘制一些连接两个数字 A[i] 和 B[j] 的直线，只要 A[i] == B[j]，且我们绘制的直线不与任何其他连线（非水平线）相交。

以这种方法绘制线条，并返回我们可以绘制的最大连线数。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EXLLCPIK-1691065715520)(https://code-thinking-1253855093.file.myqcloud.com/pics/2021032116363533.png “1035.不相交的线”)]

思路

绘制一些连接两个数字 A[i] 和 B[j] 的直线，只要 A[i] == B[j]，且直线不能相交！

直线不能相交，这就是说明在字符串A中 找到一个与字符串B相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，链接相同数字的直线就不会相交。

拿示例一A = [1,4,2], B = [1,2,4]为例，相交情况如图：

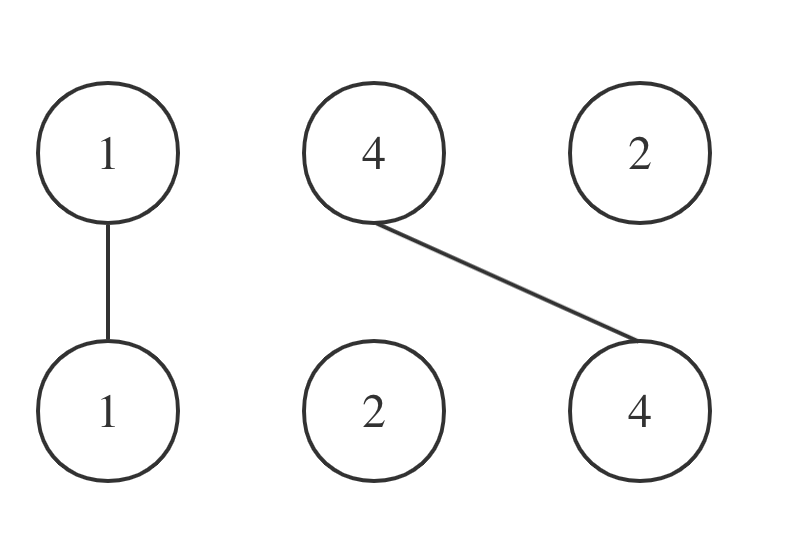
其实也就是说A和B的最长公共子序列是[1,4]，长度为2。 这个公共子序列指的是相对顺序不变（即数字4在字符串A中数字1的后面，那么数字4也应该在字符串B数字1的后面）

这么分析完之后，大家可以发现：本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度！

那么本题就和我们刚刚讲过的这道题目动态规划：1143.最长公共子序列 (opens new window)就是一样一样的了。

一样到什么程度呢？ 把字符串名字改一下，其他代码都不用改，直接copy过来就行了。

代码

class Solution {public int maxUncrossedLines(int[] nums1, int[] nums2) {int len1 = nums1.length;int len2 = nums2.length;int dp[][] = new int[len1 + 1][len2 + 1];dp[0][0] = 0;for(int i = 1; i < len1 + 1; i++){for(int j = 1; j < len2 + 1; j++){if(nums1[i - 1] == nums2[j - 1]){dp[i][j] = dp[i - 1][j - 1] + 1;}else{dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[len1][len2];}
}

最大子序和

53. 最大子数组和 - 力扣（LeetCode）

题目

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

• 输入: [-2,1,-3,4,-1,2,1,-5,4]
• 输出: 6
• 解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

思路

动规五部曲如下：

• 确定dp数组（dp table）以及下标的含义

dp[i]：包括下标i（以nums[i]为结尾）的最大连续子序列和为dp[i]。

• 确定递推公式

dp[i]只有两个方向可以推出来：

• dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和
• nums[i]，即：从头开始计算当前连续子序列和

一定是取最大的，所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);

• dp数组如何初始化

从递推公式可以看出来dp[i]是依赖于dp[i - 1]的状态，dp[0]就是递推公式的基础。

dp[0]应该是多少呢?

根据dp[i]的定义，很明显dp[0]应为nums[0]即dp[0] = nums[0]。

• 确定遍历顺序

递推公式中dp[i]依赖于dp[i - 1]的状态，需要从前向后遍历。

• 举例推导dp数组

以示例一为例，输入：nums = [-2,1,-3,4,-1,2,1,-5,4]，对应的dp状态如下： [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LOBioPxG-1691065715521)(https://code-thinking-1253855093.file.myqcloud.com/pics/20210303104129101.png “53.最大子序和（动态规划）”)]

注意最后的结果可不是dp[nums.size() - 1]！ ，而是dp[6]。

dp[i]的定义：包括下标i（以nums[i]为结尾）的最大连续子序列和为dp[i]，这里并不是 0 - i 区间最大的连续子序列和，是以nums[i]为结尾的最大连续子序列和，所以最后的值不一定是最大的

在回顾一下dp[i]的定义：包括下标i之前的最大连续子序列和为dp[i]。

那么我们要找最大的连续子序列，就应该找每一个i为终点的连续最大子序列。

所以在递推公式的时候，可以直接选出最大的dp[i]。

代码

class Solution {public int maxSubArray(int[] nums) {if(nums.length == 0) return 0;if(nums.length == 1) return nums[0];// dp[i]：包括下标i（以nums[i]为结尾）的最大连续子序列和为dp[i]。int dp[] = new int[nums.length];dp[0] = nums[0];int res = dp[0];for(int i = 1; i < nums.length; i++){dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);res = Math.max(res, dp[i]);}return res;}
}