文章目录
- 最优化问题引入
- 凸集
- 凸函数
- 凸优化
- 梯度
- Jacobi矩阵
- Hessian矩阵
最优化问题引入
例如:有一根绳子,长度一定的情况下,需要如何围成一个面积最大的图像?这就是一个最优化的问题。就是我们高中数学中最常见的最值问题。
最优化问题的一般形式是:
m i n f ( x ) x ∈ C minf(x) \\ x \in C minf(x)x∈C
其中, f f f是目标函数, A A A是约束条件, x x x是参数值。要求解最优化问题,就是要找到一个可行解 x ∗ x^∗ x∗,使得对于所有的 x ∈ A x\in A x∈A,都有 f ( x ∗ ) ≤ f ( x ) f(x^∗)≤f(x) f(x∗)≤f(x)。
最优化问题的三个基本要素是:
- 目标函数:用来衡量结果的好坏
- 参数值:未知的因子,需要通过数据来确定
- 约束条件:需要满足的限制条件
凸集
定义:集合 C C C中任意两点的线 C C C中,则称集合 C C C为凸集,也即满足 ∀ x , y ∈ C , 0 ≤ 0 ≤ 1 \forall x,y\in C,0≤0≤1 ∀x,y∈C,0≤0≤1有 8 x + ( 1 − ) y ∈ C 8x+(1-)y\in C 8x+(1−)y∈C的集合称为凸集。
凸集合就是一个集合中的任意两点之间的线段都属于这个集合,而非凸集合就是不满足这个条件的集合。
凸集合:
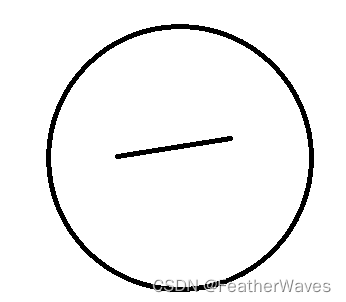
非凸集合:
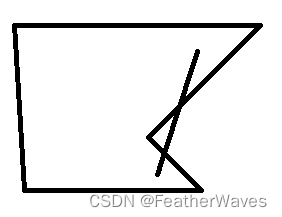
凸函数
定义:凸函数是一种定义在凸集上的实值函数,满足任意两点连成的线段上的函数值不大于两点的函数值的加权平均。也就是说,如果 f f f是凸函数,那么对于任意 x x x和 y y y在定义域内,以及任意 θ θ θ在 ( 0 , 1 ) (0,1) (0,1)之间,有
f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y) f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)
这个不等式称为凸函数的凸性条件。如果不等式中的等号只在 x = y x=y x=y时成立,那么 f f f是严格凸的。如果不等式反向成立,那么 f f f是凹函数。如果 f f f既是凸函数又是凹函数,那么 f f f是仿射函数。
二维空间的凸函数:
import numpy as np
import matplotlib.pyplot as plt# 定义凸函数 f(x) = x^2
def f(x):return x**2# 生成x轴的数据
x = np.linspace(-5, 5, 100)# 计算y轴的数据
y = f(x)# 画出函数图像
plt.plot(x, y)# 设置坐标轴标签和标题
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Convex Function')# 显示图像
plt.show()
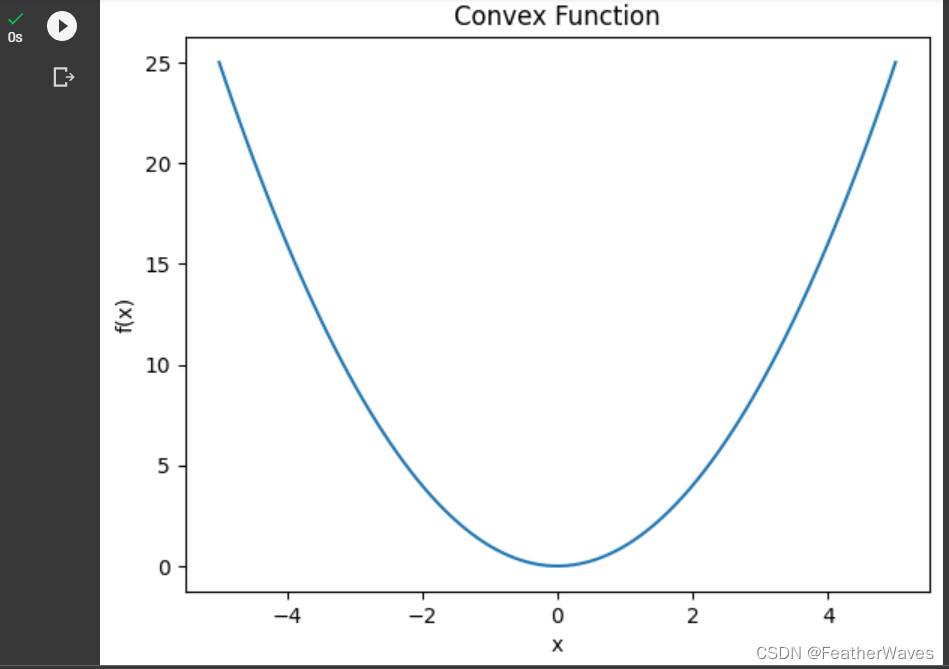
三维空间的凸函数:
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np# 定义凸函数 f(x,y) = x^2 + y^2
def f(x, y):return x**2 + y**2# 生成x和y轴的数据
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)# 将x和y轴数据转换为网格矩阵
X, Y = np.meshgrid(x, y)# 计算z轴的数据
Z = f(X, Y)# 创建3D图像对象
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')# 画出函数图像
ax.plot_surface(X, Y, Z)# 设置坐标轴标签和标题
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x,y)')
ax.set_title('Convex Function')# 显示图像
plt.show()
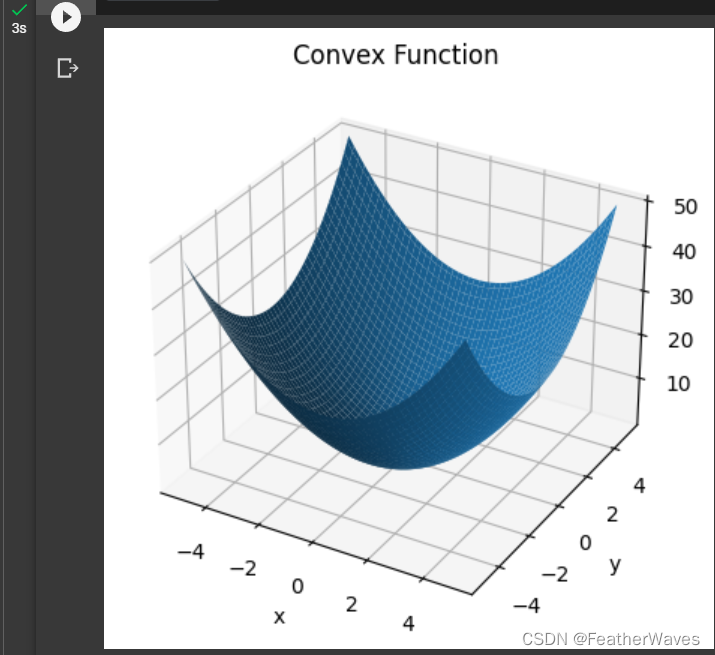
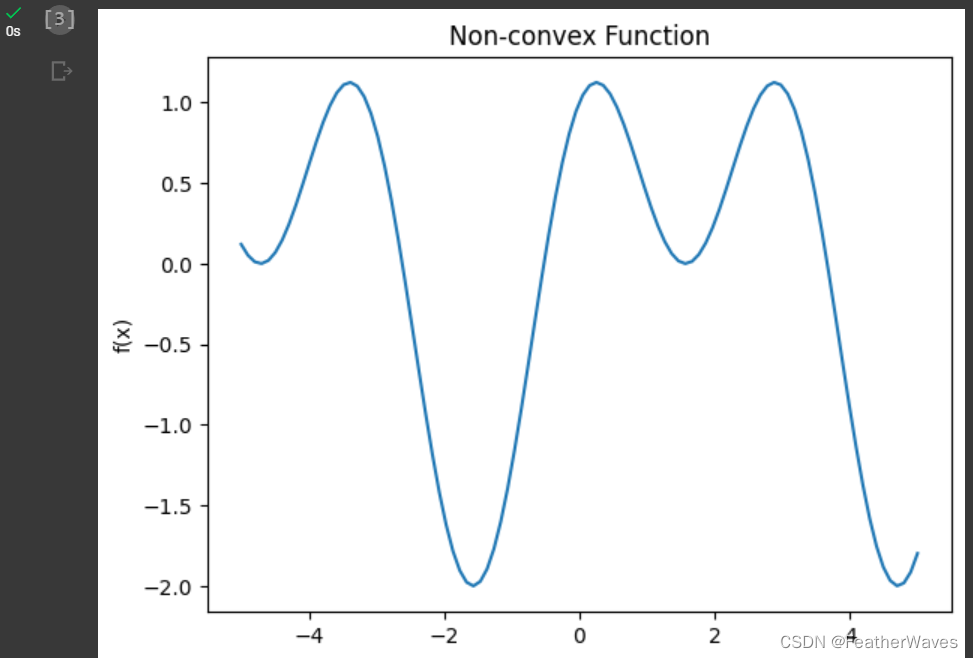
二维空间的非凹非凸函数:
import numpy as np
import matplotlib.pyplot as plt# 定义非凹非凸函数 f(x) = sin(x) + cos(2x)
def f(x):return np.sin(x) + np.cos(2*x)# 生成x轴的数据
x = np.linspace(-5, 5, 100)# 计算y轴的数据
y = f(x)# 画出函数图像
plt.plot(x, y)# 设置坐标轴标签和标题
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Non-convex Function')# 显示图像
plt.show()
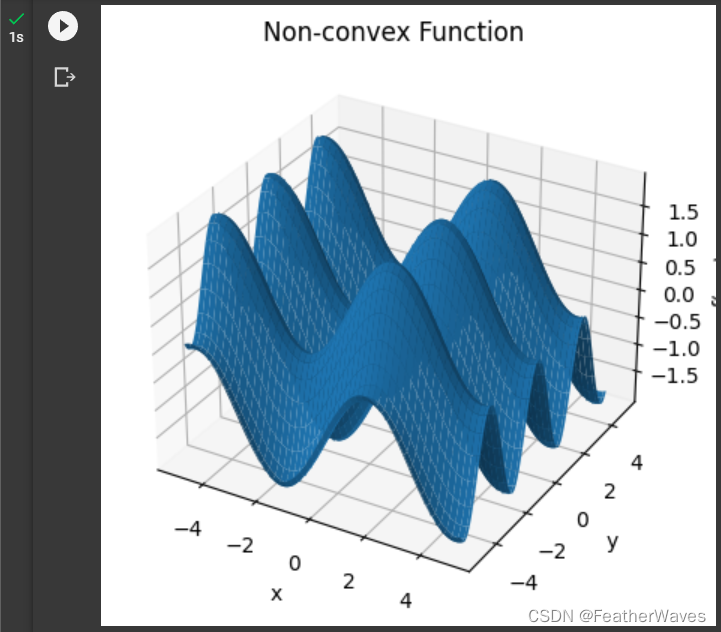
三维空间的非凹非凸函数:
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np# 定义非凹非凸函数 f(x,y) = sin(x) + cos(2y)
def f(x, y):return np.sin(x) + np.cos(2*y)# 生成x和y轴的数据
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)# 将x和y轴数据转换为网格矩阵
X, Y = np.meshgrid(x, y)# 计算z轴的数据
Z = f(X, Y)# 创建3D图像对象
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')# 画出函数图像
ax.plot_surface(X, Y, Z)# 设置坐标轴标签和标题
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x,y)')
ax.set_title('Non-convex Function')# 显示图像
plt.show()
凸优化
凸优化是数学最优化的一个子领域,研究定义在凸集中的凸函数最小化的问题。
凸优化问题可以形式化地写成:
m i n f ( x ) s . t . g i ( x ) ≤ 0 , i = 1 , 2 , ⋯ , m h j ( x ) = 0 , j = 1 , 2 , ⋯ , n \begin{align*} min&f(x) \\ s.t. &g_i(x)≤0,i=1,2,\cdots,m\\ &h_j(x)=0,j=1,2,\cdots,n \end{align*} mins.t.f(x)gi(x)≤0,i=1,2,⋯,mhj(x)=0,j=1,2,⋯,n
其中x为优化变量; f f f为凸目标函数; g i g_i gi和 h j h_j hj为约束函数,分别表示不等式约束和等式约束;
这个问题的意思是求解最小化目标函数 f ( x ) f(x) f(x),使得x满足不等式约束 g i ( x ) ≤ 0 g_i(x)≤0 gi(x)≤0和等式约束 h j ( x ) = 0 h_j(x)=0 hj(x)=0。
一个凸优化问题具备如下性质:
- 凸优化的局部极小点就是全局极小点:
- 如果目标函数是严格凸函数,则凸优化问题具有唯一的全局极小点:
- 凸优化的全局极大点必定能在可行域的边界上达到;
梯度
它表示一个多元函数在某一点沿着最大增长方向的变化率,可以用偏导数来表示。梯度是一个向量,它的方向是函数在该点最大增长的方向,它的大小是在该方向上的增长率。梯度可以用向量微分算子(nabla)来表示。
例如:
∇ f ( x , y ) = ∂ f ∂ x i + ∂ f ∂ y j \nabla f(x,y) = \frac{\partial f}{\partial x}i+\frac{\partial f}{\partial y}j ∇f(x,y)=∂x∂fi+∂y∂fj
Jacobi矩阵
定义: 雅可比矩阵是一个函数的一阶偏导数以一定方式排列成的矩阵,其行列式称为雅可比行列式。雅可比矩阵反映了一个函数在给定点的最佳线性逼近,类似于单变量函数的导数。如果函数是从 R n ℝ_n Rn到 R m ℝ_m Rm的映射,那么它的雅可比矩阵是一个 m × n m \times n m×n的矩阵,可以用以下方式定义:
J = [ ∂ f 1 ∂ x 1 ⋯ ∂ f 1 ∂ x n ⋮ ⋱ ⋮ ∂ f m ∂ x 1 ⋯ ∂ f m ∂ x n ] J = \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n} \end{bmatrix} J= ∂x1∂f1⋮∂x1∂fm⋯⋱⋯∂xn∂f1⋮∂xn∂fm
其中 f i f_i fi是函数的第 i i i个分量, x j x_j xj是第 j j j个自变量。雅可比矩阵的符号表示为 J f J_f Jf或者 ∂ ( f 1 , ⋯ , f m ) ∂ ( x 1 , ⋯ , x m ) \frac{\partial {(f_1,\cdots, f_m)}}{\partial {(x_1,\cdots, x_m)}} ∂(x1,⋯,xm)∂(f1,⋯,fm)。雅可比矩阵的第 i i i行是由函数 f i f_i fi的梯度向量表示的。
举例:
设有函数 F : R 3 → R 4 F:ℝ^3 \to ℝ^4 F:R3→R4,其分量为:
w = x + y + z x = x y = y z = z w=x+y+zx=xy=yz=z w=x+y+zx=xy=yz=z
雅可比矩阵是:
J ( F ) = ∣ ∂ w ∂ x ∂ w ∂ y ∂ w ∂ z ∂ x ∂ x ∂ x ∂ y ∂ x ∂ z ∂ y ∂ x ∂ y ∂ y ∂ y ∂ z ∂ z ∂ x ∂ z ∂ y ∂ z ∂ z ∣ J(F) = \begin{vmatrix} \frac{\partial w}{\partial x} & \frac{\partial w}{\partial y} & \frac{\partial w}{\partial z} \\ \frac{\partial x}{\partial x} & \frac{\partial x}{\partial y} & \frac{\partial x}{\partial z} \\ \frac{\partial y}{\partial x} & \frac{\partial y}{\partial y} & \frac{\partial y}{\partial z} \\ \frac{\partial z}{\partial x} & \frac{\partial z}{\partial y} & \frac{\partial z}{\partial z} \end{vmatrix} J(F)= ∂x∂w∂x∂x∂x∂y∂x∂z∂y∂w∂y∂x∂y∂y∂y∂z∂z∂w∂z∂x∂z∂y∂z∂z
将给定的函数代入上式子,得到:
J ( F ) = ∣ 1 1 1 y x 0 0 z y 0 0 1 ∣ J(F) = \begin{vmatrix} 1 & 1 & 1 \\ y & x & 0 \\ 0 & z & y\\ 0 & 0 & 1 \end{vmatrix} J(F)= 1y001xz010y1
Hessian矩阵
H e s s i a n Hessian Hessian矩阵是一个多元函数的二阶偏导数构成的方阵,用于描述函数的局部曲率。如果函数 f : R n → R f:R^n→R f:Rn→R在点 x x x处具有连续的二阶偏导数,那么它的 H e s s i a n Hessian Hessian矩阵 H f ( x ) H_f(x) Hf(x)定义为:
H f ( x ) = [ ∂ 2 f ∂ x 1 2 ( x ) ⋯ ∂ 2 f ∂ x 1 ∂ x n ( x ) ⋮ ⋱ ⋮ ∂ 2 f ∂ x n ∂ x 1 ( x ) ⋯ ∂ 2 f ∂ x n 2 ( x ) ] H_f(x) = \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2}(x) & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n}(x) \\ \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n \partial x_1}(x) & \cdots & \frac{\partial^2 f}{\partial x_n^2}(x) \end{bmatrix} Hf(x)= ∂x12∂2f(x)⋮∂xn∂x1∂2f(x)⋯⋱⋯∂x1∂xn∂2f(x)⋮∂xn2∂2f(x)
H e s s i a n Hessian Hessian矩阵和 J a c o b i Jacobi Jacobi矩阵之间的关系是, H e s s i a n Hessian Hessian矩阵等于函数的梯度的 J a c o b i Jacobi Jacobi矩阵。也就是说,如果 f : R n → R f:Rn→R f:Rn→R,那么
H f ( x ) = J ∇ f ( x ) H_f(x)=J_{\nabla f}(x) Hf(x)=J∇f(x)
其中 ∇ f \nabla f ∇f表示函数f的梯度, J ∇ f J_{\nabla f} J∇f表示梯度 ∇ f \nabla f ∇f的 J a c o b i Jacobi Jacobi矩阵。这个关系可以从 H e s s i a n Hessian Hessian矩阵和 J a c o b i Jacobi Jacobi矩阵的定义直接得到。
举例:
有个二元函数是 f ( x , y ) = x 2 + y 2 f(x,y)=x2+y2 f(x,y)=x2+y2。它的梯度是 ∇ f ( x , y ) = ( 2 x , 2 y ) ∇f(x,y)=(2x,2y) ∇f(x,y)=(2x,2y),它的 H e s s i a n Hessian Hessian矩阵是
J ( F ) = ∣ ∂ 2 f ∂ x 2 ( x , y ) ∂ 2 f ∂ x ∂ y ( x , y ) ∂ 2 f ∂ y ∂ x ( x , y ) ∂ 2 f ∂ y 2 ( x , y ) ∣ = ∣ 2 0 0 2 ∣ J(F) = \begin{vmatrix} \frac{\partial^2 f}{\partial x^2}(x, y) & \frac{\partial^2 f}{\partial x \partial y} (x, y)\\ \frac{\partial^2 f}{\partial y \partial x}(x, y) & \frac{\partial^2 f}{\partial y^2} (x, y) \end{vmatrix} = \begin{vmatrix} 2 & 0 \\ 0 & 2 \end{vmatrix} J(F)= ∂x2∂2f(x,y)∂y∂x∂2f(x,y)∂x∂y∂2f(x,y)∂y2∂2f(x,y) = 2002
它的梯度的 J a c o b i Jacobi Jacobi矩阵是
J ( F ) = ∣ ∂ ∂ x ( 2 x ) ∂ ∂ y ( 2 x ) ∂ ∂ x ( 2 y ) ∂ ∂ y ( 2 y ) ∣ = ∣ 2 0 0 2 ∣ J(F) = \begin{vmatrix} \frac{\partial }{\partial x}(2x) & \frac{\partial }{\partial y}(2x) \\ \frac{\partial }{\partial x}(2y) & \frac{\partial }{\partial y}(2y) \end{vmatrix} = \begin{vmatrix} 2 & 0 \\ 0 & 2 \end{vmatrix} J(F)= ∂x∂(2x)∂x∂(2y)∂y∂(2x)∂y∂(2y) = 2002
可以看出,它们是相等的。