LBP,局部二值模式(Local Binary Pattern),是一种描述图像局部纹理特征的方式,具有旋转不变性和灰度不变性。首先由T. Ojala, M.Pietikäinen, 和 D. Harwood 在1994年提出。
LBP特征描述
基础LBP算子
基础的LBP算子定义为在3*3的窗口内,以窗口中心像素为阈值,将相邻的8个像素的灰度值与其进行比较,若周围像素值大于中心像素值,则该像素点的位置被标记为1,否则为0。这个方法和前面提到的Brief描述子由点类似,二进制的值都是对比像素值大小出来的。、

如上图所示,3x3窗口中有8个相邻的像素。这8个像素和中心像素进行对比可以得到8个二进制值,这8个bit就被用来表示中心点的纹理信息。根据bit权重值窗口可以得知,对应二进制为11100001(最高有效位在左边,如果最高有效位在右边,则是10000111),对应十进制的225,计算过程的起点是左上角的像素按顺时针方向计算。
计算的过程的数学表达式如下:

其中s(x)定义如下:

这个过程其实就是上图表达的意思。
LBP改进:圆形LBP
基础的LBP算子覆盖的区域非常小,不能满足不同尺寸的纹理特征描述需求。因此Ojala改进了LBP算子,将3x3的区域扩展为任意半径的圆形,在半径为 R 的圆形邻域内有任意多个像素点,记为,R表示半径大小,p表示采样点的个数。

以上图的为例,它表示半径为1的圆上取8个采样点生成LBP描述符。需要注意的是,随着半径的增大,采样点像素和中心像素的相关度会降低。
LBP等价模式(Uniform Patterns)
对于有P个采样点的LBP来说,LBP对应的二进制数总共有个可能的值。随着采样点数量的增加,值的个数会增长的很快。如此多的模式会对纹理提取和分类造成不利影响。为了解决这个问题,Ojala提出了“等价模式(Uniform Patterns)”。对于一个二进制串,按照首尾相接的环的方式,统计其bit跳变的次数。如果跳变次数最多只有两次,则称为等价模式,否则称为混合模式(hybrid pattern)。
以P=8为例来说:00000000(0次跳变),01110000(2次跳变),11001111(2次跳变),这几个都是等价模式。11001001(4次跳变)和01010010(6次跳变)则不是等价模式。使用下面的方法来检查模式是否是等价模式:

从公式中的第一个 可以看出,是计算了串的首尾bit是否有跳变的。网上有些文章举的例子比如00001111跳变次数只有1次,从目前我看到的资料看(也许是我看的资料有错?)感觉是有问题的。
对于P = 8,总共有58个等价模式(7 * 8 + 2,2是因为全0和全1都是等价模式,推导过程其实考虑到如果要跳变次数不超过两次,1的位置必须是紧挨着的这一点就可以了),其形式如下图:
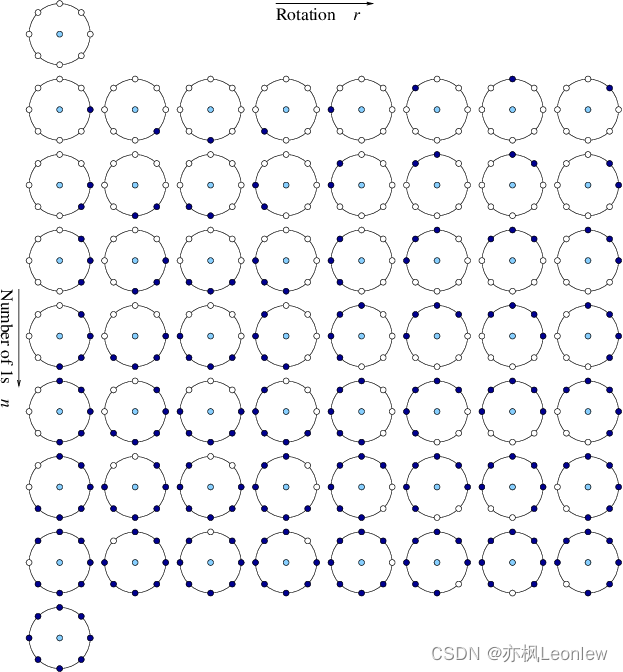

因此,等价模式把LBP值分为59类,58个uniform pattern为一类,其它的所有值为第59类。这样直方图从原来的256维变成59维。这使得特征向量的维数更少,并且可以减少高频噪声带来的影响。
具有旋转不变性的LBP
LBP算子本身具有灰度不变性(结果的0或1反映了灰度的相对强弱,而不是绝对的灰度差异),但无论是基础的LBP算子和运行LBP算子都不具有旋转不变性。为了让LBP具有旋转不变性,Maenpaa等人又将 LBP算子进行了扩展,提出了具有旋转不变性的 LBP 算子。
旋转不变的LBP算子通过不断旋转圆形邻域得到多个LBP值,取其中的最小值作为该邻域的 LBP 值。局部旋转不变的LBP模式定义如下:

ROR是旋转函数。
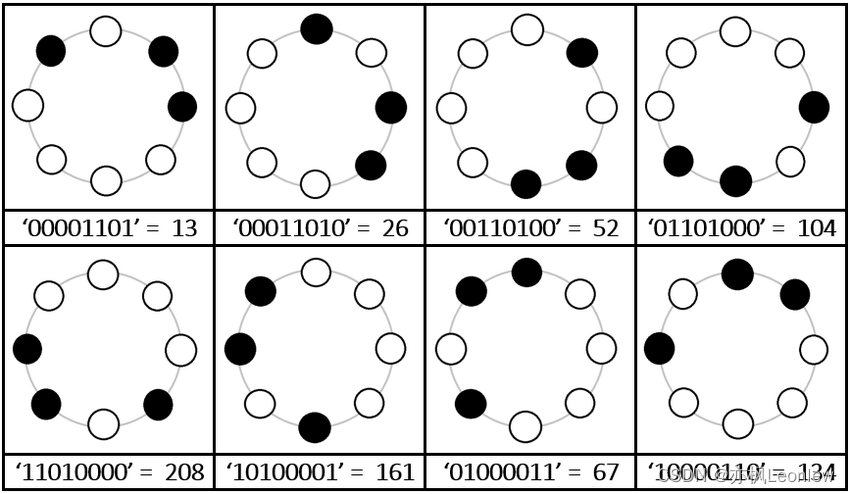
如上图所示,对于P=8的情况,总共计算了8个LBP值,其中13最小,会作为最终的LBP值使用。
对于旋转不变的LBP,加上等价模式,得到的表达式如下:

参考资料
https://www.researchgate.net/publication/259166826_Research_and_Perspective_on_Local_Binary_Pattern![]() https://www.researchgate.net/publication/259166826_Research_and_Perspective_on_Local_Binary_Pattern
https://www.researchgate.net/publication/259166826_Research_and_Perspective_on_Local_Binary_Pattern
https://www.researchgate.net/publication/305152373_Texture_Feature_Extraction_by_Using_Local_Binary_Pattern![]() https://www.researchgate.net/publication/305152373_Texture_Feature_Extraction_by_Using_Local_Binary_PatternTowards Understanding the Formation of Uniform Local Binary PatternsThe research reported in this paper focuses on the modeling of Local Binary Patterns (LBPs) and presents an apriori model where LBPs are considered as combinations of permutations. The aim is to increase the understanding of themechanisms related to the formation of uniform LBPs. Uniform patterns are known to exhibit high discriminativecapability; however, so far the reasons for this have not been fully explored. We report an observation that although the overall apriori probability of uniform LBPs is high, it is mostly due to the high probability of only certain classes of patterns, whilethe a priori probability of other patterns is very low. In order to examine this behavior, the relationship between the runs upand down test for randomness of permutations and the uniform LBPs was studied. Quantitative experiments were then carriedout to show that the relative effect of uniform patterns to the LBP histogram is strengthened with deterministic data, in comparisonwith the i.i.d. model. This was verified by using an a priori model as well as through experiments with natural image data. It was further illustrated that specific uniform LBP codes can also provide responses to salient shapes, that is, to monotonically changing intensity functions and edges within the image microstructure.
https://www.researchgate.net/publication/305152373_Texture_Feature_Extraction_by_Using_Local_Binary_PatternTowards Understanding the Formation of Uniform Local Binary PatternsThe research reported in this paper focuses on the modeling of Local Binary Patterns (LBPs) and presents an apriori model where LBPs are considered as combinations of permutations. The aim is to increase the understanding of themechanisms related to the formation of uniform LBPs. Uniform patterns are known to exhibit high discriminativecapability; however, so far the reasons for this have not been fully explored. We report an observation that although the overall apriori probability of uniform LBPs is high, it is mostly due to the high probability of only certain classes of patterns, whilethe a priori probability of other patterns is very low. In order to examine this behavior, the relationship between the runs upand down test for randomness of permutations and the uniform LBPs was studied. Quantitative experiments were then carriedout to show that the relative effect of uniform patterns to the LBP histogram is strengthened with deterministic data, in comparisonwith the i.i.d. model. This was verified by using an a priori model as well as through experiments with natural image data. It was further illustrated that specific uniform LBP codes can also provide responses to salient shapes, that is, to monotonically changing intensity functions and edges within the image microstructure.https://www.hindawi.com/journals/isrn/2013/429347/http://kiwi.bridgeport.edu/cpeg585/LocalBinaryPattern_Tutorial.pdf
![]() http://kiwi.bridgeport.edu/cpeg585/LocalBinaryPattern_Tutorial.pdfhttps://www.researchgate.net/publication/220809357_Rotation_Invariant_Image_Description_with_Local_Binary_Pattern_Histogram_Fourier_Features
http://kiwi.bridgeport.edu/cpeg585/LocalBinaryPattern_Tutorial.pdfhttps://www.researchgate.net/publication/220809357_Rotation_Invariant_Image_Description_with_Local_Binary_Pattern_Histogram_Fourier_Features![]() https://www.researchgate.net/publication/220809357_Rotation_Invariant_Image_Description_with_Local_Binary_Pattern_Histogram_Fourier_Features
https://www.researchgate.net/publication/220809357_Rotation_Invariant_Image_Description_with_Local_Binary_Pattern_Histogram_Fourier_Features