💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
奇异频谱分析(SSA)是一种信号分解技术,旨在将信号扩展为可解释且具有物理意义的组件(例如,正弦波,噪声等)。本文介绍了SSA可分离性的新理论和实践结果,并介绍了一种滑动SSA的新方法。首先,将SSA与无监督分类算法相结合,提供了一种全自动的数据驱动的成分提取方法,我们在理论研究中研究了组分分离的局限性。其次,采用详细的自动SSA方法设计了一种基于滑动分析窗口的方法,在分析具有时变分量的非平稳信号时,该方法比经典SSA方法提供了更好的结果。最后,将所提出的滑动SSA方法与经验模态分解和同步挤压短时傅里叶变换进行了比较,该方法应用于合成信号和真实信号。
原文摘要:
Singular spectrum analysis (SSA) is a signal decomposition technique that aims at expanding signals into interpretable and physically meaningful components (e.g., sinusoids, noise, etc.). This paper presents new theoretical and practical results about the separability of the SSA and introduces a new method called sliding SSA. First, the SSA is combined with an unsupervised classification algorithm to provide a fully automatic data-driven component extraction method for which we investigate the limitations for components separation in a theoretical study. Second, the detailed automatic SSA method is used to design an approach based on a sliding analysis window, which provides better results than the classical SSA method when analyzing nonstationary signals with a time-varying number of components. Finally, the proposed sliding SSA method is compared to the empirical mode decomposition and to the synchrosqueezed short-time Fourier transform, applied on both synthetic and real-world signals.
📚2 运行结果

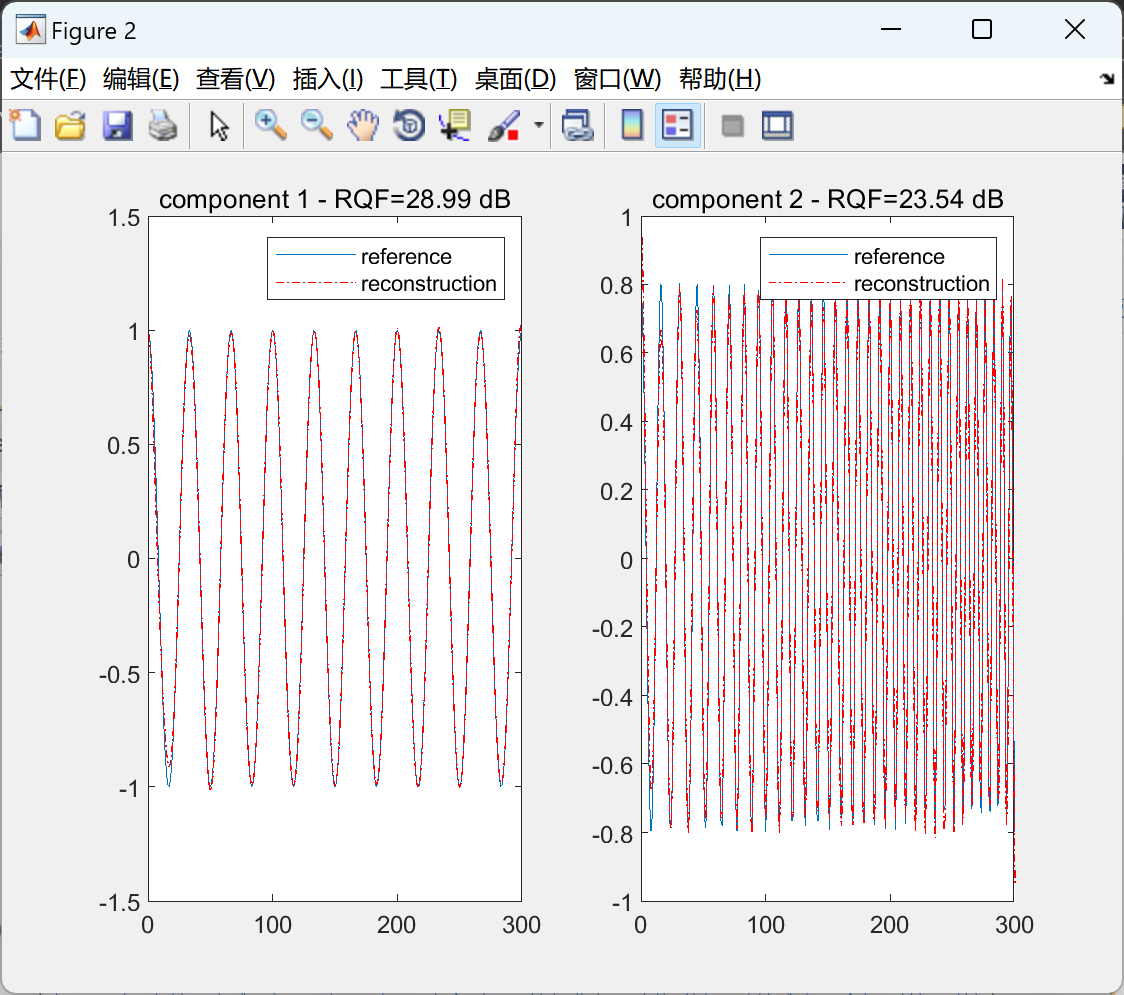
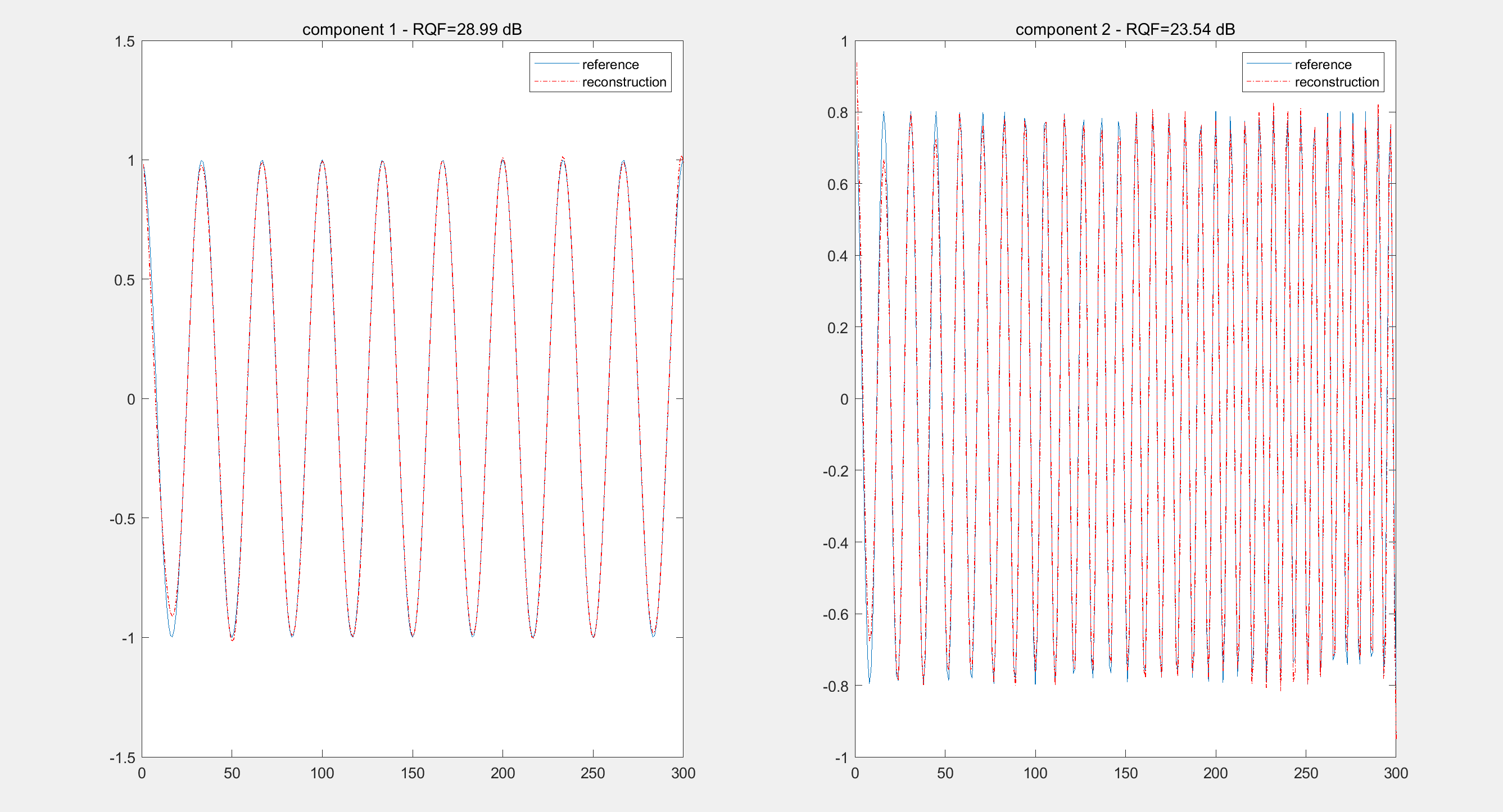
部分代码:
%% 3 Display results
figure
plot(xn)
title(sprintf('observed mixture - SNR=%.2f dB', RQF(x, xn)))
saveas(gcf,'../output/observation.png')
figure
for i = 1:nc
subplot(1,nc, i)
plot(s(:,i))
hold on
plot(Y(:,i), 'r-.')
legend('reference', 'reconstruction')
title(sprintf('component %d - RQF=%.2f dB', i, RQF(s(:,i), Y(:,i))))
end
saveas(gcf,'../output/components.png')
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[J. Harmouche, D. Fourer, P. Flandrin, F. Auger and P. Borgnat. One
or Two Components ? The Singular Spectrum Analysis answers. Proc. SLRA'2015. Grenoble, France.June 2015]
[J. Harmouche, D. Fourer, P. Flandrin, F. Auger and P. Borgnat. Une ou deux composantes: