1.简述
白平衡
白平衡的英文为White Balance,其基本概念是“不管在任何光源下,都能将白色物体还原为白色”,对在特定光源下拍摄时出现的偏色现象,通过加强对应的补色来进行补偿。
所谓的白平衡是通过对白色被摄物的颜色还原(产生纯白的色彩效果),进而达到其他物体色彩准确还原的一种数字图像色彩处理的计算方法。(源自百度百科)
灰度世界算法
灰度世界理论:认为任何一幅图像, 当有足够的色彩变化时, 其R, G, B分量均值会趋于平衡(即 RGB三个数值相等, 也就是说应当是黑白灰类型的颜色)。这个理论在全局白平衡中得到⼴泛应用, 特点是能够利用更多的图像信息来做判断, 但在面对⾊色彩较为单一的图像时就显得有些乏力了。
灰度世界算法:根据灰度世界理论,将原始图的RGB均值分别调整到R= G = B即可。不完美的地方就是这个算法对颜色不丰富的图像敏感程度一般,处理起来效果也就不会很理想,局限性很大。
2.代码
%% 学习目标:平衡方程用于图像
function anisodiffusionsimple()
a = imread('trui.tif');
a = im2double(a);
g1 =a;
g2 =a;
stepsize1=.2;
stepsize2=.1;
nosteps=200;
verbose=1;
if verbose
figure(verbose);
subplot(2,3,1); imshow(g1); title('Original Image'); drawnow;
end
h=waitbar(0,'Now is doing Diffusion');
for i=1:nosteps
laplaceg1=snldStep1(g1);
g1 = g1 +stepsize1 * laplaceg1;
laplaceg2=snldStep2(g2);
g2 = g2 +stepsize2 * laplaceg2;
waitbar(i/nosteps,h);
if verbose
figure(verbose);
subplot(2,3,2); imshow(uint8(255*(laplaceg1-min(laplaceg1(:)))/(max(laplaceg1(:))-min(laplaceg1(:)))));
%subplot(2,2,2); imshow(uint8(255*(laplaceg-min(laplaceg(:)))/(max(laplaceg(:))-min(laplaceg(:)))));%归一化?
title('Laplace term')
subplot(2,3,3); imshow(g1);
title('Anisotropic Diffusion'); drawnow;
subplot(2,3,5); imshow(uint8(255*(laplaceg2-min(laplaceg2(:)))/(max(laplaceg2(:))-min(laplaceg2(:)))));
%subplot(2,2,2); imshow(uint8(255*(laplaceg-min(laplaceg(:)))/(max(laplaceg(:))-min(laplaceg(:)))));%归一化?
title('Laplace term')
subplot(2,3,6); imshow(g2);
title('Isotropic Diffusion'); drawnow;
end
waitbar(i/nosteps,h);
end
close(h);
function r = snldStep1( L )
% Discrete numerical scheme of dL/dt for scalar diffusion
N = size(L, 1);
M = size(L, 2);
lamda=.008;
% Set delta_x,delta_y=2,so we can set delta_x/2=delta_y/2=1
Lpc = translateImage( L, 1, 0 );
Lmc = translateImage( L, -1, 0 );
Lcp = translateImage( L, 0, 1 );
Lcm = translateImage( L, 0, -1 );
Lppc = translateImage( L, 2, 0 );
Lmmc = translateImage( L, -2, 0 );
Lcpp = translateImage( L, 0, 2 );
Lcmm = translateImage( L, 0, -2 );
Lap_i = (Lpc+Lcp)-2*L; % Laplace_I
d =abs( Lap_i/lamda );
e=-d.*d;
C = exp(e);
Cpc = translateImage( C, 1, 0 );
Cmc = translateImage( C, -1, 0 );
Ccp = translateImage( C, 0, 1 );
Ccm = translateImage( C, 0, -1);
r = ( 1/4*(Cpc.*( Lppc - L )-Cmc.*( L - Lmmc ))+1/4*(Ccp.*( Lcpp - L )-Ccm.*( L - Lcmm )) );
function k = snldStep2( L )
% Discrete numerical scheme of dL/dt for scalar diffusion
N = size(L, 1);
M = size(L, 2);
Lpc = translateImage( L, 1, 0 );
Lmc = translateImage( L, -1, 0 );
Lcp = translateImage( L, 0, 1 );
Lcm = translateImage( L, 0, -1 );
k = ( (Lpc-2*L+Lmc)+ (Lcp-2*L+Lcm) );
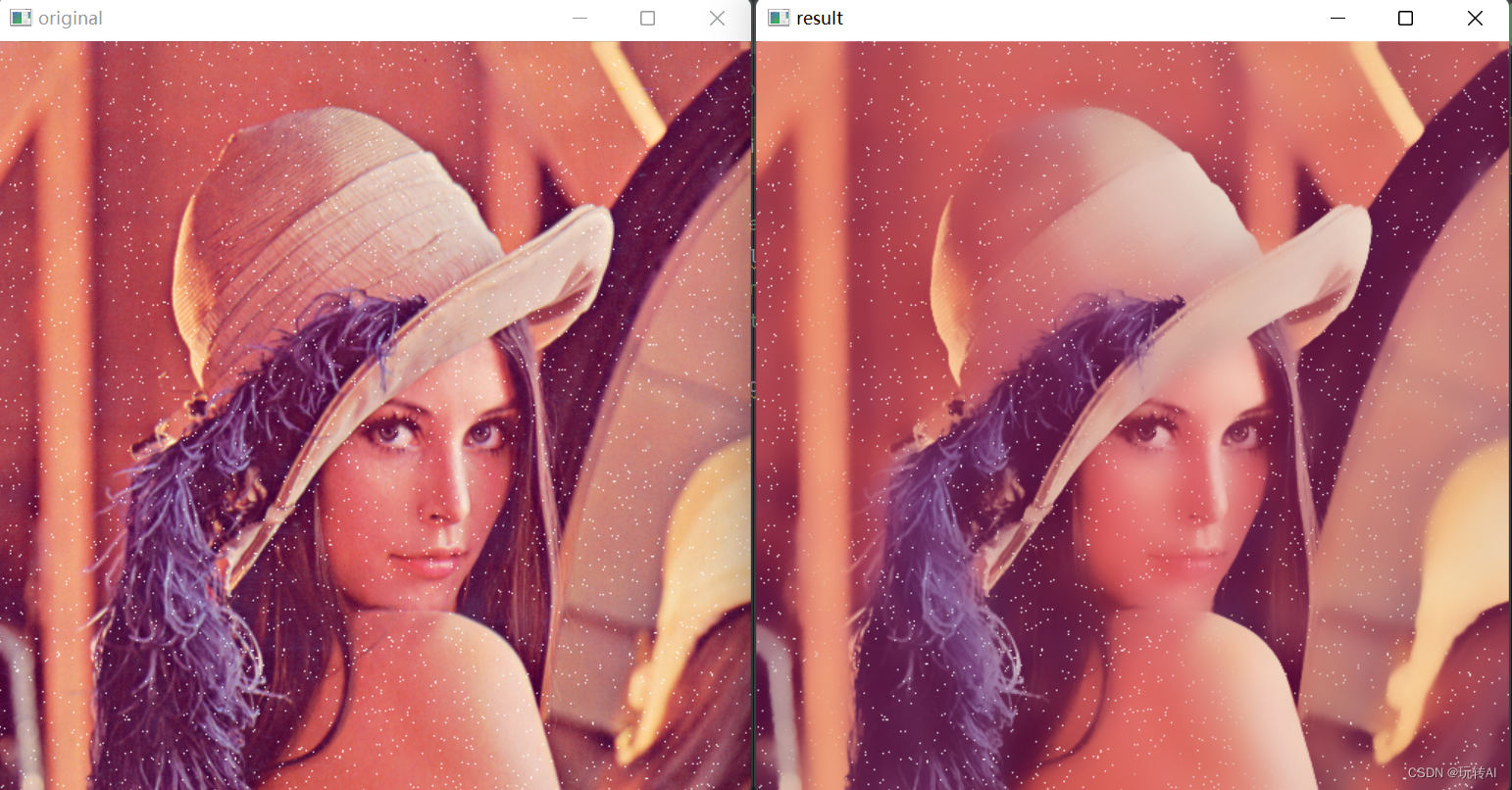
3.运行结果