给定两个整数数组
preorder和inorder,其中preorder是二叉树的先序遍历,inorder是同一棵树的中序遍历,请构造二叉树并返回其根节点。
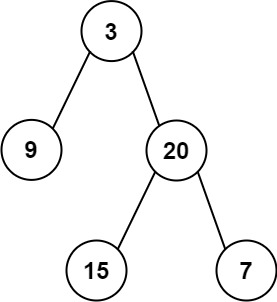
题目中是给定两个数组,一个是存放这颗树的前序遍历的数组,一个是存放这棵树的中序遍历的数组,解这道题的关键我们首先要知道树的前中序遍历分别指的是什么?它们两者之间到底存在着什么关系?解下来让我们一探究竟
前序遍历:
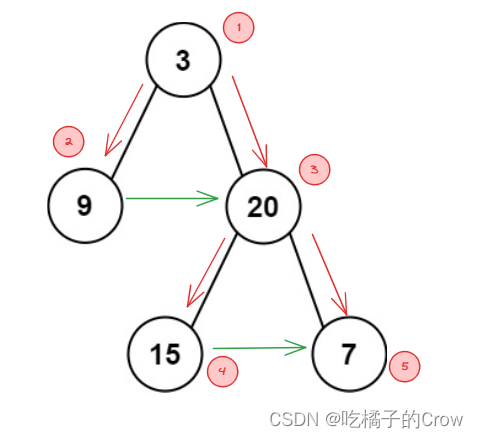
前序遍历的遍历顺序是中左右,先遍历自己,后遍历自己的左子树,最后再遍历自己的右子树,由上图已知该树的前序遍历为[3,9,20,15,7]
中序遍历:

中序遍历的遍历顺序是左中右,先遍历左子树,后遍历自己,最后再遍历自己的右子树,由上图已知该树的中序遍历为[9,3,15,20,7]

观看这两个数组,有没有发现什么特别的地方?

树是一种天然的递归结构,每棵子树也可以称为一棵独立的树,根据上图我们不难发现,数组中的元素是严格按照中左右的顺序填充的

根据上图我们不难发现,数组中的元素是严格按照中左右的顺序填充的
所以我们再来看这两个数组的特点:
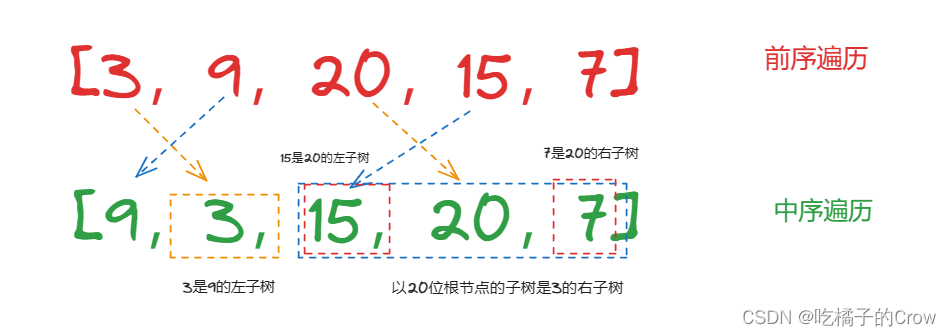
我们已经得知了这两个数组中的相存的特点,接下来就可以撸代码了
- 我们要通过数组中的元素值得到该元素在数组中的索引为位置,所们先要使用Map结构的数据结构去对我们的中序遍历时的数据进行预处理
Map<Integer,Integer> map=new HashMap<>();for(int i=0;i<inorder.length;i++){map.put(inorder[i],i);}- 然后开始我们的构建函数dfs(前序数组,前序开始的位置,前序结束的位置,中序数组,中序开始的位置,中序结束的位置)
return dfs(preorder,0,preorder.length-1,inorder,0,inorder.length-1);- 递归时如果出先了开始位置比结束位置还要大的时候,这种情况肯定是不满足我们的条件的,所以直接抛出null就可以了
if(pStart>pEnd||iStart>iEnd){return null;}- 通过前序遍历数组拿到我们相对根节点,然后通过map去查询我们中序数组中我们的相对根节点的索引index,因为我们的中序遍历是左中右,所以中序遍历中的index-iStart的长度就是我们相对子树的节点的个数
int val=preorder[pStart];TreeNode root=new TreeNode(val);int size=map.get(val);int length=size-iStart;- 最后开始dfs,构造左右子树,这道题就完成了
// 不包括当前的根结点 前序取不到起点(左开右闭) 中序取不到终点(左闭右开)root.left=dfs(preorder,pStart+1,pStart+length,inorder,iStart,size-1);// 左子树下一次递归的起点 root.right=dfs(preorder,pStart+length+1,pEnd,inorder,size+1,iEnd);// 右子树下一次递归的起点接下来上源码供大家参考:
Map<Integer,Integer> map=new HashMap<>();public TreeNode buildTree(int[] preorder, int[] inorder) {if(preorder==null||inorder==null){return null;}for(int i=0;i<inorder.length;i++){map.put(inorder[i],i);}return dfs(preorder,0,preorder.length-1,inorder,0,inorder.length-1);}public TreeNode dfs(int[] preorder,int pStart,int pEnd,int[]inorder,int iStart,int iEnd){if(pStart>pEnd||iStart>iEnd){return null;}int val=preorder[pStart];TreeNode root=new TreeNode(val);int size=map.get(val);int length=size-iStart;root.left=dfs(preorder,pStart+1,pStart+length,inorder,iStart,size-1);root.right=dfs(preorder,pStart+length+1,pEnd,inorder,size+1,iEnd);return root;}