在这篇博客文章中，我们将深入研究 去噪扩散概率模型(也称为 DDPM，扩散模型，基于分数的生成模型或简单的 自动编码器) ，因为研究人员已经能够用它们在(非)条件图像/音频/视频生成方面取得显著成果。最受欢迎的例子(在写这篇文章的时候)包括由 OpenAI 设计的 GLIDE 和 DALL-E 2，由海德堡大学设计的 潜扩散，以及由谷歌大脑设计的 ImageGen。

DDPM理论回顾

生成扩散模型DDPM如下图所示分为前向、逆向两个过程，它首先通过不断往原始清晰数据中添加噪声使其变成标准高斯噪声（前向过程），而后期望从标准高斯噪声中还原原始数据（逆向过程）。若能实现，那便可从已知的标准高斯分布中采样一个噪声数据，而后利用DDPM模型生成符合原始数据分布的新数据。

Diffusion模型包含两个过程：

1. 逆向过程（Reverse Process）：也称为去噪过程（denoising diffusion）。如果知道逆向过程的每一步的真实分布$q(x_{t-1}|x_t)$，那么从一个随机噪声$x_T\sim \mathcal{N}\left(x;0,\mathrm{I}\right)$开始，逐渐去噪就能生成一个真实的样本，所以逆向过程也就是生成数据的过程。
2. 正向过程（Forward Process）：也就是加噪过程、扩散(diffusion)过程。对于给定的现实世界中存在的真实图像${\mathbf{x}}_0$，我们对其一步步加噪声，得到${\mathbf{x}}_1$，${\mathbf{x}}_2$，…，最后得到完全的高斯噪声${\mathbf{x}}_T$。前向过程的存在意义是帮助神经网络去学习逆向过程，也就是训练用的。
   更仔细想想的话，前向过程里得到的噪声其实就是"生成标签"的过程，因为在这一过程中，已经有了真实的图像，并且生成了真实图像加噪后的结果；那么自然就可能让网络学习这样一个映射，即从有噪声的图像中恢复原始图像。

前置知识

数学符号：$y\propto x$：y正比于x，即y随着x增大而线性增大。
条件概率：

• $p(A|B)$表示事件B已经发生的情况下，事件A发生的可能性。也就是说变量B已知的情况下，变量A的取值分布。
• $p(A|B,C)$表示在B、C同时发生的情况下，事件A发生的概率。也就是说变量B、C已知确定的情况下，变量A的取值分布。

贝叶斯公式：$p(A|B)=\frac{p(B|A)\times p(A)}{p(B)}$

高斯分布的概率密度函数：给定均值为$\mu$，标准差为$\sigma$，方差为${\sigma }^2$的高斯分布$N(\mu ,{\sigma }^2)$，其概率密度函数(PDF)为：$p(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$。很多时候为了方便也会写成$p(x)\propto e^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$，也就是把前面乘的常数$\frac{1}{\sqrt{2\pi }}$去掉。进一步地，为了方便推导，把$e^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$展开，因此有$p(x)\propto exp(-\frac{1}{2}(\frac{1}{{\sigma }^2}{x}^2-\frac{2\mu }{{\sigma }^2}x+\frac{{\mu }^2}{{\sigma }^2}))$

概率分布中分号的理解，对形如$q(x_t|x_{t-1})=N(X_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_t\mathrm{I})$的式子的理解如下：
$f(x)$其实就是一个函数，输入变量值$x$，在经过规则 $f$ 处理后，最终拿到一个结果。另一种常见的情况，比如概率分布$P(x)$，其本质上也是一个以 $x$ 为自变量的函数，在变量$X$的值为$x$的情况下，拿到一个结果，这个结果的意义为变量$X$取到$x$的概率。而$f(x;\theta )$，其实意思就是$f(x)$，只不过强调函数的参数为$\theta$。这个$\theta$可以是某个确定的常量，也可以是多个确定常量的总体（比如深度神经网络中的全体可训练参数）。例如：${\theta }^{2}x+2\theta +1$，$\theta =3$，这个函数自变量是$x$，自然可以写成$f(x)$；又因为$x$的系数(参数)是$\theta$(某个已知或未知的确定值)，因此可以表达为$f(x;\theta )$。

根据上述内容，现在讨论一个比较复杂的情况。比如，$\mathcal{N}\left(x;0,\mathrm{I}\right)$的意思是什么？我们知道，$\mathcal{N}\left(0,\mathrm{I}\right)$表示标准高斯分布，均值为0，方差为1，其本质上也是一个概率密度函数：$f(x)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{x^2}{2}}$。从这里可以发现，一般的函数我们都是强调自变量本身(比如$x$)，而在概率论里面有时候强调的是函数参数本身(比如高斯分布的均值和方差)，而淡化了输入变量(默认为$x$，省略)。因此$\mathcal{N}\left(x;0,\mathrm{I}\right)$相比与$\mathcal{N}\left(0,\mathrm{I}\right)$的区别就在于显式强调了函数的输入为$x$。

最后再来讲一个更复杂的东西：$q\left({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1}\right)=\mathcal{N}\left({\mathbf{x}}_t;\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathrm{I}\right)$。这个公式要分多步来看。首先，函数本身是个条件概率分布，$q\left({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1}\right)$表示${\mathbf{x}}_{t-1}$已知的情况下，${\mathbf{x}}_t$的分布(${\mathbf{x}}_t$取各种值的概率)。而后面的这个高斯分布则强调了其输入自变量为${\mathbf{x}}_t$(因为是${\mathbf{x}}_t$的概率密度函数，所以自变量当然是${\mathbf{x}}_t$，而高斯分布的均值和方差则分别为$\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1}$和${\beta }_t\mathrm{I}$，与条件分布的条件${\mathbf{x}}_{t-1}$有关。

也就是说，如果概率分布密度函数中的自变量不是默认的$x$而是其他，那么应该在分布记号中显式地用分号表示实际的自变量，比如实际的自变量是$x_1$而不是$x$，那么高斯分布应该记作$\mathcal{N}(x_1;\mu ,{\sigma }^2)$。默认不写分号的话，$\mathcal{N}(\mu ,{\sigma }^2)$等价于$\mathcal{N}(x;\mu ,{\sigma }^2)$。

高斯分布的乘法与加法：

• 对标准高斯分布$\mathcal{N}(0,1)$做乘法，乘以$\sigma$，得到一个新的高斯分布，$\mathcal{N}(0,{\sigma }^2)$N。
• 对标准高斯分布$\mathcal{N}(0,1)$做加法，加上$\mu$，得到一个新的高斯分布，$\mathcal{N}(\mu ,1)$。
• 两个高斯分布$\mathcal{N}(0,{\sigma }_1^2)$，$\mathcal{N}(0,{\sigma }_2^2)$相加，得到一个新的高斯分布，$\mathcal{N}(0,{\sigma }_1^2+{\sigma }_2^2)$。

重参数化技巧：对高斯分布$\mathcal{N}(\mu ,{\sigma }^2)$进行采样一个噪声$ϵ$，等价于先从标准高斯分布$\mathcal{N}(0,1)$中采样得到一个噪声$\mathbf{z}$，乘以标准差$\sigma$，加上均值$\mu$，即：$ϵ=\mu +\mathbf{z}\cdot \sigma$，进行这一转化是为了方便网络训练。举个例子，上面我们已经得到了${\mathbf{x}}_t$是从高斯分布$\mathcal{N}(\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathbf{I})$采样出来的噪声，该高斯分布的均值为$\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1}$ ，标准差为$\sqrt{{\beta }_t}$ ，所以${\mathbf{x}}_t=\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1}+\sqrt{{\beta }_t}\mathbf{z}$。

过程详解

Forward Process

前向过程也称为扩散过程，将真实数据逐步变成噪声。比方说，给定一张原始图像${\mathbf{x}}_0$，对其加一次「标准」高斯噪声$\mathbf{z}\sim \mathcal{N}(0,\mathbf{I})$，得到${\mathbf{x}}_1$。记${\mathbf{x}}_i$为对原始图像加 $i$ 次噪声后的结果，可以发现，当 $i$ 足够大的时候，数据会被高斯噪声淹没，变成纯正的高斯噪声。

第一个问题，加多少次噪声？在文中，其由一个超参数$T$控制，即步数。原文$T=1000$，即对原始图像加1000次噪声后，其会变成完全的高斯噪声。
第二个问题，噪声怎么加？因为加噪过程本质是加权和，比如$0.8\times Image+0.1\times Noise$，会涉及到一个权重的问题(注意，我们后面会看到，图像的权重与噪声的权重相加并不需要为1)。在文章中，噪声的这个权重有个专有的名词，叫做扩散率，记为$\beta$，比如可以从0.0001逐步插值到0.02。从这里可以看到，加噪是一个逐步的过程，对图像原有的信息是慢慢破坏的(扩散率很低)。这样主要是为了方便网络在逆扩散过程中学习去噪，如果对信息一次破坏太多那么网络可能就无法学会怎么去复原了。

为什么扩散率是逐渐增大的呢？可以反过来理解，在加噪声的过程中，扩散率逐渐增大，对应着在去噪声的过程中，扩散率逐渐减小——也就是说，去噪的过程是先把"明显"的噪声给去除，对应着较大的扩散率；当去到一定程度，逐渐逼近真实真实图像的时候，去噪速率逐渐减慢，开始微调，也就是对应着较小的扩散率。

现在来看扩散过程的初步数学定义 。给定当前具有一定噪声的图像${\mathrm{x}}_{t-1}$，加入标准高斯噪声${\mathbf{z}}_{t-1}\sim \mathcal{N}(0,\mathbf{I})$，得到进一步加噪的图像${\mathbf{x}}_t$，有：$${\mathbf{x}}_t=\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1}+\sqrt{{\beta }_t}{\mathbf{z}}_{t-1}$$这个公式其实就是上面提到的$a\times \text{Image}+b\times \text{Noise}$，其中$\text{Image}$为${\mathbf{x}}_{t-1}$，$\text{Noise}$为${\mathbf{z}}_{t-1}$。

但是，论文中提到了下面的式子，也就是概率分布的形式：$$q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})=\mathcal{N}({\mathbf{x}}_t;\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathbf{I})$$需要注意的是${\mathbf{x}}_t=\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1}+\sqrt{{\beta }_t}{\mathbf{z}}_{t-1}$与$q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})=\mathcal{N}({\mathbf{x}}_t;\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathbf{I})$是等价的。这可以从前面介绍的重参数化技巧中可知，$ϵ=\mu +\mathbf{z}\cdot \sigma$表示的就是从$ϵ\sim \mathcal{N}(\mu ,{\sigma }^2)$中采样的过程。据此，同样就可以将${\mathbf{x}}_t$改写为从$q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})$中采样的形式。

进一步地，用人话来说，有：

1. 因为加噪声是一个带有随机性的过程（噪声是随机的），所以${\mathbf{x}}_t$是可以写成概率分布形式的，即$q({\mathbf{x}}_t)$，并且该分布是一个高斯分布$\mathcal{N}$（加入的是高斯噪声）；
2. 又因为是给定了${\mathbf{x}}_{t-1}$，才能知道${\mathbf{x}}_t$，所以这个分布还是一个条件分布，即$q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})$。
3. 此外，这个高斯分布是有关于当前变量${\mathbf{x}}_t$的条件分布，因此会记作$\mathcal{N}({\mathbf{x}}_t;a,b)$而非$\mathcal{N}(a,b)$。
4. 关于${\beta }_t$，之前提到的扩散率$\beta$是插值得到的，会不断变化，因此落实到加噪第$t$步过程的$\beta$则记为${\beta }_t$。

现在解决第三个问题：给定原始图像${\mathbf{x}}_0$，能不能一步到位计算得到加噪$t$次后的${\mathbf{x}}_t$？答案是可以的。首先看结论：$${\mathbf{x}}_t=\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}{\tilde{\mathbf{z}}}_t$$其中${\alpha }_t=1-{\beta }_t$, $\overline{{\alpha }_t}={\alpha }_1\times ...\times {\alpha }_t=\prod _{i=1}^t{\alpha }_i$，${\tilde{\mathbf{z}}}_t\sim \mathcal{N}(0,\mathbf{I})$。这样，当想求一个$t$很大的${\mathbf{x}}_{\mathbf{t}}$时，就省去了逐步模拟的步骤。

可以发现，当$t$很大时，$\sqrt{{\bar{\alpha }}_t}$会很接近0，最终的结果${\mathbf{x}}_t$几乎完全由噪声${\tilde{\mathbf{z}}}_t$所取代，但仍然保留了十分微弱的原始图像${\mathbf{x}}_0$。也就是说，只要方法巧妙，理论上还是可以通过逐步去噪的方式得到${\mathbf{x}}_t$中隐藏的${\mathbf{x}}_0$。

推导过程：$$\begin{array}{c}\begin{array}{rl}{\mathbf{x}}_t& =\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1}+\sqrt{1-{\alpha }_t}{\mathbf{z}}_{t-1}\\ & =\sqrt{{\alpha }_t{\alpha }_{t-1}}{\mathbf{x}}_{t-2}+\sqrt{{\alpha }_t(1-{\alpha }_{t-1})}{\mathbf{z}}_{t-2}+\sqrt{1-{\alpha }_t}{\mathbf{z}}_{t-1}\\ & =\sqrt{{\alpha }_t{\alpha }_{t-1}}{\mathbf{x}}_{t-2}+\sqrt{1-{\alpha }_t{\alpha }_{t-1}}{\bar{\mathbf{z}}}_{t-2}\\ & =...\\ & =\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}{\tilde{\mathbf{z}}}_t\end{array}\end{array}$$上面式子中各种$\mathbf{z}$的变体都满足标准高斯分布$\mathcal{N}(0,1)$。第一行到第二行是把${\mathbf{x}}_{t-1}=\sqrt{{\alpha }_{t-1}}{\mathbf{x}}_{t-2}+\sqrt{1-{\alpha }_{t-1}}{\mathbf{z}}_{t-2}$给换进去。主要比较难理解的地方在于第二行到第三行，$\sqrt{{\alpha }_t\left(1-{\alpha }_{t-1}\right)}{\mathbf{z}}_{t-2}+\sqrt{1-{\alpha }_t}{\mathbf{z}}_{t-1}$是怎么变成$\sqrt{1-{\alpha }_t{\alpha }_{t-1}}{\bar{\mathbf{z}}}_{t-2}$ 的，解释如下：

对于任意两个正态分布$\mathbf{x}\sim \mathcal{N}({\mu }_1,{\sigma }_1^2)$和$\mathbf{y}\sim \mathcal{N}({\mu }_2,{\sigma }_2^2)$，根据前面介绍的公式，它们的和的分布为$\mathbf{x}+\mathbf{y}\sim \mathcal{N}({\mu }_1+{\mu }_2,{\sigma }_1^2+{\sigma }_2^2)$，因此，对于两个标准正态分布${\mathbf{z}}_{t-2}$和${\mathbf{z}}_{t-1}$，将其前面乘上一个系数得到：$\sqrt{{\alpha }_t-{\alpha }_t{\alpha }_{t-1}}{\mathbf{z}}_{t-2}\sim \mathcal{N}(0,{\alpha }_t-{\alpha }_t{\alpha }_{t-1}),\sqrt{1-{\alpha }_t}{\mathbf{z}}_{t-1}\sim \mathcal{N}(0,1-{\alpha }_t)$，因此$\sqrt{{\alpha }_t-{\alpha }_t{\alpha }_{t-1}}{\mathbf{z}}_{t-2}+\sqrt{1-{\alpha }_t}{\mathbf{z}}_{t-1}\sim \mathcal{N}(0,1-{\alpha }_t{\alpha }_{t-1})$，也即$\sqrt{1-{\alpha }_t{\alpha }_{t-1}}{\bar{\mathbf{z}}}_{t-2}$。这里不同形式的$\mathbf{z}$单纯起区分作用，本质上都属于标准正态分布$\mathcal{N}(0,\mathrm{I})$的不同采样。

以上就是前向过程大概内容，从前向过程得到的${\mathbf{x}}_t$将会作为标签，帮助网络学习如何从${\mathbf{x}}_T$中一步步去噪，最终得到${\mathbf{x}}_0$。

Reverse Process

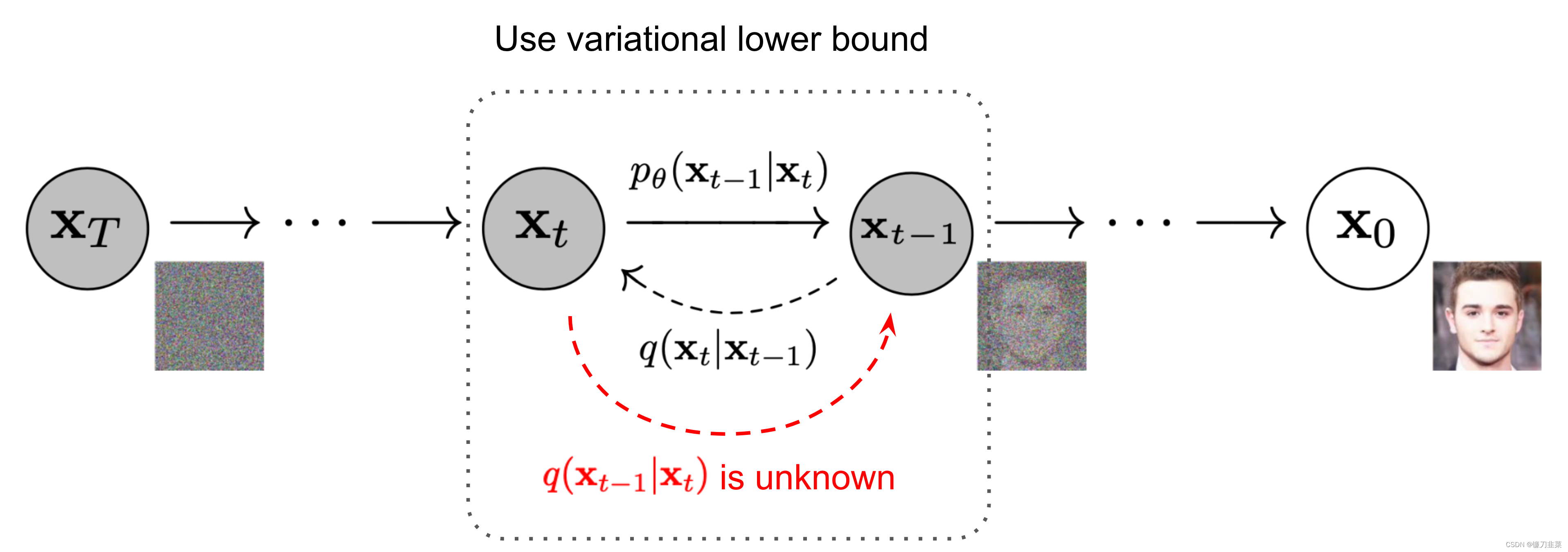
后向过程又称逆扩散过程。我们希望能够从一个噪声分布${\mathbf{x}}_T$中逐步去预测出来目标分布${\mathbf{x}}_0$。后向过程仍然是一个马尔科夫链过程。根据我们输入的${\mathbf{x}}_t$去求${\mathbf{x}}_{t-1}$的分布，即求$$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t)$$，直接对该公式求解比较困难，可以使用贝叶斯公式将其转化为我们已知的量，因为加噪过程$q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})$是已知的，因此有$$q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)=\frac{q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})\times q({\mathbf{x}}_{t-1})}{q({\mathbf{x}}_t)}$$

现在就出现了一个问题，虽然$q({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1})$我们是知道了，但是$q({\mathbf{x}}_t)$和$q({\mathbf{x}}_{t-1})$我们不知道。需要特别注意的是，当$T$足够大的时候，可以认为$q({\mathbf{x}}_T)$就是标准高斯噪声，这个是可以知道的；而由于$t$并不知道是多少，可能是个很小的值，这种情况下$q({\mathbf{x}}_t)$中包含了大量的原始图像信息，因此$q({\mathbf{x}}_t)$是不知道的。

要想知道加了一定噪声的图像$q({\mathbf{x}}_t)$和$q({\mathbf{x}}_{t-1})$，自然就依赖于一个先决条件，没加噪声的图像$q({\mathbf{x}}_0)$。换句话说，$q({\mathbf{x}}_t\mid {\mathbf{x}}_0)$和$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_0)$是知道的，因此对式子$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t)=\frac{q({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1})\times q({\mathbf{x}}_{t-1})}{q({\mathbf{x}}_t)}$再加上一个条件${\mathbf{x}}_0$，得到一个多元条件分布，即：$$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0)=\frac{q({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1},{\mathbf{x}}_0)\times q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_0)}{q({\mathbf{x}}_t\mid {\mathbf{x}}_0)}$$
其实上面这个式子还可以继续变一下。由于扩散过程是一个马尔可夫过程，因此${\mathbf{x}}_t$只和${\mathbf{x}}_{t-1}$有关，和${\mathbf{x}}_0$无关，即$q({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1},{\mathbf{x}}_0)=q({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1})$，有：
$$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0)=\frac{q({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1})\times q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_0)}{q({\mathbf{x}}_t\mid {\mathbf{x}}_0)}$$
可以发现一个问题，在测试阶段，${\mathbf{x}}_0$本身是我们要求的东西，是未知的；因此上面这个式子只有在训练阶段${\mathrm{x}}_0$已知的情况下才能运转起来。为了让测试阶段也能用，对上面式子进一步分析，也就是看一下能否将${\mathbf{x}}_0$消除掉。如果可以消除，就不用陷入到这种要算${\mathbf{x}}_0$还要必须知道${\mathbf{x}}_0$的窘境。

由于正态分布$\mathcal{N}(\mu ,{\sigma }^2)$的概率密度函数$$p(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{1}{2}(\frac{x-\mu }{\sigma }{)}^2}\propto exp(-\frac{1}{2}(\frac{x-\mu }{\sigma }{)}^2)=exp(-\frac{1}{2}(\frac{1}{{\sigma }^2}{x}^2-\frac{2\mu }{{\sigma }^2}x+\frac{{\mu }^2}{{\sigma }^2}))$$，故

• $q({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1})$等价于${\mathbf{x}}_t=\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1}+\sqrt{1-{\alpha }_t}{\mathbf{z}}_{t-1}$。写成概率分布的形式为$\mathcal{N}({\mathbf{x}}_t;\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1},(1-{\alpha }_t)\mathbf{I})$，进一步写成概率密度函数的形式，得到$q({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1})\propto exp(-\frac{1}{2}\frac{({\mathbf{x}}_t-\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1}{)}^2}{1-{\alpha }_t})$
• $q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_0)$等价于${\mathbf{x}}_{t-1}=\sqrt{{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_{t-1}}{\tilde{\mathbf{z}}}_{t-1}$，利用重参数技巧，则$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_0)=\mathcal{N}({\mathbf{x}}_{t-1};\sqrt{{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0,(1-{\bar{\alpha }}_{t-1})\mathbf{I})\propto exp(-\frac{1}{2}\frac{({\mathbf{x}}_{t-1}-\sqrt{{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0{)}^2}{1-{\bar{\alpha }}_{t-1}})$
• $q({\mathbf{x}}_t\mid {\mathbf{x}}_0)$等价于${\mathbf{x}}_t=\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}{\tilde{\mathbf{z}}}_t$，同样利用重参数技巧，则$q({\mathbf{x}}_t\mid {\mathbf{x}}_0)=\mathcal{N}({\mathbf{x}}_t;\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0,(1-{\bar{\alpha }}_t)\mathbf{I})\propto exp(-\frac{1}{2}\frac{({\mathbf{x}}_t-\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0{)}^2}{1-{\bar{\alpha }}_t})$

这样一来对概率分布的运算就可以转化为指数运算。由于对指数进行乘除运算相当于对其系数的加减运算，也就是说，两个分布相乘，可以认为就是对其密度函数相加；两个分布相除，可以认为就是对其密度函数相减。因此，$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0)=q({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1})\times q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_0)/q({\mathbf{x}}_t\mid {\mathbf{x}}_0)$，写成密度函数的形式，有：
$$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0)\propto \exp (-\frac{1}{2}[\frac{({\mathbf{x}}_t-\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1}{)}^2}{{\beta }_t}+\frac{({\mathbf{x}}_{t-1}-\sqrt{{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0{)}^2}{1-{\bar{\alpha }}_{t-1}}-\frac{({\mathbf{x}}_t-\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0{)}^2}{1-{\bar{\alpha }}_t}])$$

现在，要对上面这个式子进行进一步的整理，看看能不能得到什么有用的东西来。首先把括号里的平方展开来试一试：
$$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0)\propto \exp (-\frac{1}{2}[\frac{{\mathbf{x}}_t^2-2\sqrt{{\alpha }_t}{\mathbf{x}}_t{\mathbf{x}}_{t-1}+{\alpha }_t{\mathbf{x}}_{t-1}^2}{{\beta }_t}+\frac{{\mathbf{x}}_{t-1}^2-2\sqrt{{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0{\mathbf{x}}_{t-1}+{\bar{\alpha }}_{t-1}{\mathbf{x}}_0^2}{1-{\bar{\alpha }}_{t-1}}-\frac{{\mathbf{x}}_t^2-2\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0{\mathbf{x}}_t+{\bar{\alpha }}_t{\mathbf{x}}_0^2}{1-{\bar{\alpha }}_t}])$$

接下来的操作就是比较有技巧性的了。回到最初的问题，由于我们的目标是为了求于${\mathbf{x}}_{t-1}$有关的条件分布$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0)$。基于这一直觉，把上式的${\mathbf{x}}_{t-1}$给提取整理出来，得到：
$$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0)\propto \exp (-\frac{1}{2}[(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}}){\mathbf{x}}_{t-1}^2-(\frac{2\sqrt{{\alpha }_t}}{{\beta }_t}{\mathbf{x}}_t+\frac{2\sqrt{{\bar{a}}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0){\mathbf{x}}_{t-1}+C({\mathbf{x}}_t,{\mathbf{x}}_0)])$$

注意$C({\mathbf{x}}_t,{\mathbf{x}}_0)$是一个和${\mathbf{x}}_{t-1}$无关的部分，所以省略。由于$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0)$服从于正态分布，所以只需要找到其均值和方差就能求出其分布。怎么求？根据高斯分布的概率密度函数定义和上述结果（配平方），我们可以得到分布$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0)$的均值和方差。

现在，尝试将${\mathbf{x}}_{t-1}$的均值和方差给求出来。根据$\mathcal{N}(x;\mu ,{\sigma }^2)\propto \exp (-\frac{1}{2}\left(\frac{1}{{\sigma }^2}{x}^2-\frac{2\mu }{{\sigma }^2}x+\frac{{\mu }^2}{{\sigma }^2}\right))$，发现，方差${\sigma }^2$就是$x^2$系数的倒数；而${\mathbf{x}}_{t-1}^2$的系数为$\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}}$，可以发现，其完全只由人工确定的超参数$\alpha$和$\beta$所确定，因此方差是已知的，即
$${\tilde{\beta }}_t=\frac{1}{(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}})}=\frac{1}{\frac{({\alpha }_t-{\alpha }_t{\bar{\alpha }}_{t-1}+{\beta }_t)}{{\beta }_t(1-{\bar{\alpha }}_{t-1})}}$$根据前文的定义$\overline{{\alpha }_t}={\alpha }_1\times ...\times {\alpha }_t$ ,可知${\alpha }_t{\bar{\alpha }}_{t-1}=\overline{{\alpha }_t}$，而且${\alpha }_t=1-{\beta }_t$, 所以有：$${\tilde{\beta }}_t=\frac{1}{\frac{({\alpha }_t-{\bar{\alpha }}_t+{\beta }_t)}{{\beta }_t(1-{\bar{\alpha }}_{t-1})}}=\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t$$

而对于均值，其值与${\mathbf{x}}_{t-1}$的系数$\frac{2\sqrt{{\alpha }_t}}{{\beta }_t}{\mathbf{x}}_t+\frac{2\sqrt{{\bar{a}}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0$ 有关。可以发现，除了已知量$\alpha$，$\beta$，${\mathbf{x}}_t$，依然包含着我们想要消除的项${\mathbf{x}}_0$。

但是对于${\mathbf{x}}_0$，由于现在是处于后向过程，${\mathbf{x}}_0$是未知的，现在要想办法将${\mathbf{x}}_0$用已知量进行替换。现在，将均值$\mu$写成一个关于${\mathbf{x}}_t$与${\mathbf{x}}_0$的函数，记做${\tilde{\mathbf{\mu }}}_t\left({\mathbf{x}}_t,{\mathbf{x}}_0\right)$ 。将$$\frac{1}{{\sigma }^2}=(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}})$$ 代入$$\frac{2\mu }{{\sigma }^2}=(\frac{2\sqrt{{\alpha }_t}}{{\beta }_t}{\mathbf{x}}_t+\frac{2\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0)$$求解得到：
$${\tilde{\mathbf{\mu }}}_t\left({\mathbf{x}}_t,{\mathbf{x}}_0\right)=\frac{\sqrt{{\alpha }_t}\left(1-{\bar{\alpha }}_{t-1}\right)}{1-{\bar{\alpha }}_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}{\mathbf{x}}_0$$做到这一步，我们已经把求解
$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0)$这一复杂的问题，转化为怎么去求解该分布的均值$\mu$的问题。而要求$\mu$，就得想办法把复杂的${\mathbf{x}}_0$给消掉或简化，有没有办法把${\mathbf{x}}_0$化简成一个更容易看懂的形式呢？

回想一下，在前向过程中已经得到了${\mathbf{x}}_0$和${\mathbf{x}}_t$的关系$${\mathbf{x}}_t=\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}{\tilde{\mathbf{z}}}_t$$我们直接把${\mathbf{x}}_0$给移动到等式左边，得到：
$${\mathbf{x}}_0=\frac{1}{\sqrt{{\bar{\alpha }}_t}}\left({\mathbf{x}}_t-\sqrt{1-{\bar{\alpha }}_t}{\tilde{\mathbf{z}}}_t\right)$$然后把${\mathbf{x}}_0$带入到${\tilde{\mathbf{\mu }}}_t\left({\mathbf{x}}_t,{\mathbf{x}}_0\right)$中，最终得到$${\tilde{\mu }}_t({\mathbf{x}}_t)=\frac{1}{\sqrt{{\alpha }_t}}({\mathbf{x}}_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{\tilde{\mathbf{z}}}_t)$$这样我们就把${\mathbf{x}}_0$消掉了，现在我们只要知道了${\tilde{\mathbf{z}}}_t$，就能将${\tilde{\mu }}_t$表示出来，进而得到$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0)$的分布，将${\mathbf{x}}_{t-1}$采样出来，完成一次去噪过程。那么${\tilde{\mathbf{z}}}_t$怎么求呢？

问题是，${\tilde{\mathbf{z}}}_t$ 本身也是训练阶段，加噪过程中涉及到的东西。在测试阶段，对于一个全新采样的噪声，并不知道其是由一张图像与具体哪个高斯噪声给合成出来的(采样有无数种可能)。而且，从数学推导的角度，${\tilde{\mathbf{z}}}_t$作为一个噪声，已经非常原子了，没法将其转换成更易获得的形式。

因此，这时就需要深度学习来解决了，神经网络擅长的就是这种人力解不出但是可以通过算法去逼近的东西。也就是说，设计一个网络$\mathbf{ϵ}({\mathbf{x}}_t,t)$，希望其能够预测${\tilde{\mathbf{z}}}_t$。

• 网络的输入为当前图像${\mathbf{x}}_t$与加噪步数$t$。这里需要$t$，可以理解为只有在知道$t$的情况下才存在${\mathbf{x}}_t$的说法。
• 有了这个噪声${\tilde{\mathbf{z}}}_t$，就能求出高斯分布$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t)$的均值$\mu$与方差$\sigma$(方差可以直接由超参数计算得到)。
• 有了分布$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t)$，就可以在知道当前阶段图像${\mathbf{x}}_t$的情况下，采样得到去噪图像${\mathbf{x}}_{t-1}$了。

总结逆向过程：已知当前图像${\mathbf{x}}_t$，获得去噪一步后的图像${\mathbf{x}}_{t-1}$的过程，用概率的形式写作$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t)$。用贝叶斯公式对其处理后，发现，必须在知道${\mathbf{x}}_0$的情况下才能求解$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t)$，而${\mathbf{x}}_0$本身是去噪的最终目的，因此看起来陷入了死循环。所以，尝试将${\mathbf{x}}_0$进行变形消除，最后发现只要能够求到一个噪声${\tilde{\mathbf{z}}}_t$，就能够对$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t)$进行模拟，完成逆扩散过程。其实最后网络要预测的是一个噪声，这一结论也非常符合我们对扩散模型的直觉。因为${\mathbf{x}}_t$本身是加噪声得到的，那么如果知道加的噪声是什么，自然就能把这一过程反过来。

至此，前向过程和后向过程已经推导结束了，如果想了解论文中交叉熵Loss的推导，可参考文章的解释，公式较复杂，如果不感兴趣，直接跳过即可。

DDPM算法伪代码

训练部分

对于每次迭代：

• 第二行：随机选择一张图像。从数学的角度讲，叫做从真实图像分布$q({\mathbf{x}}_0)$中采样得到一个样本${\mathbf{x}}_0$。
• 第三行：随机选择一个前向步数（加噪声次数）$t$。这个$t$是从最小步数$1$和最大步数$T$中随机抽出来的。从数学的角度讲，叫从均匀分布$1\sim T$中采样。
• 第四行：随机生成一个标准高斯噪声$ϵ$。从数学的角度讲，叫做从标准高斯分布$\mathcal{N}(0,\mathbf{I})$中采样。
• 第五行： 计算训练时损失（也就是"进行梯度下降步骤"）。$||a-b|{|}^2$的形式其实就是最常见的均方误差损失函数（Mean Square Loss）。既然是损失函数，肯定就有一个真值和一个网络的预测值。这里的真值就是实时生成的随机噪声$ϵ$，而网络预测值则是：
  $${\mathbf{ϵ}}_{\theta }\left(\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}\mathbf{ϵ},t\right)$$其中的
  $\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}\mathbf{ϵ}$是什么含义呢？回顾上文中提到的公式：
  $${\mathbf{x}}_{\mathbf{t}}=\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}{\tilde{\mathbf{z}}}_t$$而这个${\tilde{\mathbf{z}}}_t$和$ϵ$同样都是标准高斯噪声。也就是说，$\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}\mathbf{ϵ}$其实就是${\mathbf{x}}_{\mathbf{t}}$。至此，损失函数变成了这样：
  $$||ϵ-{\mathbf{ϵ}}_{\theta }\left({\mathbf{x}}_{\mathbf{t}},t\right)|{|}^2$$
  再次对第五行的理解就是，对于第二行，第三行拿到的原始图像${\mathbf{x}}_0$和加噪次数$t$，利用前向过程能够直接推出加噪结果${\mathbf{x}}_{\mathbf{t}}$出来。现在有一个网络${ϵ}_{\theta }$，我们希望其在输入加噪结果${\mathbf{x}}_{\mathbf{t}}$和加噪次数$t$后，能够预测到一个「合适的」标准高斯噪声，也就是未知的${\tilde{\mathbf{z}}}_t$。

总结一下训练过程就是给定${\mathbf{x}}_0$和随机噪声$ϵ$，然后生成一个扩散(加噪)次数$t$，进行$t$次扩散过程得到${\mathbf{x}}_t$，然后通过一个网络${ϵ}_{\theta }$来预测一个合适的噪声，也就是${\tilde{\mathbf{z}}}_t$。

但是问题来了，网络为什么要去预测一个标准高斯噪声呢？直观来讲，这种东西直接从标准高斯分布中直接采样就可以了，为什么还要单独设计一个网络去学。要想理解这一点，将损失函数的表达式重新展开来，把$ϵ$替换成熟悉的${\tilde{\mathbf{z}}}_t$；此外，由于训练阶段的${\mathbf{x}}_t$是由${\mathbf{x}}_0$和$t$直接求出来的，因此也进行相应的替换，最终把：
$$||\mathbf{ϵ}-{\mathbf{ϵ}}_{\theta }\left(\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}\mathbf{ϵ},t\right)|{|}^2$$重新改写为：
$$||{\tilde{\mathbf{z}}}_t-{\mathbf{ϵ}}_{\theta }\left({\mathbf{x}}_0,t,{\tilde{\mathbf{z}}}_t\right)|{|}^2$$这么写有什么好处呢？可以发现一个有趣的事实，在训练阶段，网络去猜测这个${\tilde{\mathbf{z}}}_t$并不是凭空的，而是事实上已经将${\tilde{\mathbf{z}}}_t$和${\mathbf{x}}_0$给混在了一起，得到了一个混沌，然后让网络去从混沌中把${\tilde{\mathbf{z}}}_t$给重新"捞出来"。

举个形象的比喻就是，与其说${\mathbf{ϵ}}_{\theta }$是一个所谓的什么去噪网络，不如说是「沙里淘金」：

图像是金，噪声是沙子。在训练阶段，把金和沙子混在一起（加噪），让网络学习怎么去把沙子从混合物中给重新分离出来（预测噪声）。至于为什么不是直接把金给拿出来…这是前面的推导决定的，求噪声要比求图像远远更容易；换句话说，如果是直接淘金，那么网络可能淘个成百上千次，准确率仍然是0，因此很难训练，所以才是淘沙。

从这里发现，网络学到的如何淘沙子的知识，是来源于沙子和金的混合物的，受原有的金（图像）的影响。这就导致，网络在猫图像上训练的去噪网络，对于一个新噪声而言去噪也只能得到各种猫，因为在训练阶段真实分布的信息被嵌入了网络中。

而在测试阶段，相当于仍是有一堆混在一起的金和沙子，这个时候没有标准答案，网络是凭借着自己的训练阶段学到的知识把沙子给淘出来，进而「间接」完成淘金的过程。

采样部分

• 第一行：从标准高斯分布中采样得到一个噪声。由于原始图像${\mathbf{x}}_0$在加$t$次噪声后得到的东西也是一个标准高斯噪声，因此这里采样的得到的结果记为${\mathbf{x}}_T$。
• 第二行：进行$T$次逆扩散过程，将图像从高斯噪声${\mathbf{x}}_T$中恢复出来。对于每次逆扩散过程：
• 第三行：随机采样一个标准高斯噪声$\mathbf{z}$。注意在最后一步的时候就不采样了，$\mathbf{z}=0$，这算是一个trick…不管这一技巧并不影响对整体的理解。
• 第四行：通过公式计算得到去噪一次的结果：$${\mathbf{x}}_{t-1}=\frac{1}{\sqrt{{\alpha }_t}}\left({\mathbf{x}}_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{\mathbf{ϵ}}_{\theta }\left({\mathbf{x}}_t,t\right)\right)+{\sigma }_t\mathbf{z}$$这个式子的理解依旧是参考前置知识中的「重参数化技巧」。从分布的角度，比方说，从$\mathcal{N}(\mu ,{\sigma }^2)$中采样得到一个$ϵ$，写成数学表达式就是：
  $$ϵ=\mu +\mathbf{z}\cdot \sigma$$其中$\mathbf{z}$为标准高斯噪声。根据上文中的结论，我们知道高斯分布$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t)$的均值${\mu }_t$为$$\frac{1}{\sqrt{{\alpha }_t}}\left({\mathbf{x}}_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{\tilde{\mathbf{z}}}_t\right)$$，再加上方差${\sigma }_t^2$ (可以由超参数$\alpha$和$\beta$直接求得)，有：
  $$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t)\sim \mathcal{N}(\frac{1}{\sqrt{{\alpha }_t}}({\mathbf{x}}_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{\tilde{\mathbf{z}}}_t,{\sigma }_t^2)$$而${\tilde{\mathbf{z}}}_t$，其实就是网络${\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t)$能够预测的东西，直接替换掉就行。
  从分布$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t)$中采样得到${\mathbf{x}}_{t-1}$，有：
  $${\mathbf{x}}_{t-1}=\frac{1}{\sqrt{{\alpha }_t}}\left({\mathbf{x}}_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{\mathbf{ϵ}}_{\theta }\left({\mathbf{x}}_t,t\right)\right)+{\sigma }_t\mathbf{z}$$

总结一下

DDPM对Deep Unsupervised Learning using Nonequilibrium Thermodynamics文中提出的模型（下文称扩散模型）改进了两点

• 第一点，扩散模型在后向过程中，是由${\mathbf{x}}_t$预测${\mathbf{x}}_{t-1}$，也即直接预测图像，而DDPM是预测在前向过程中，我们从${\mathbf{x}}_{t-1}$扩散到${\mathbf{x}}_t$所加的噪声，有点类似Resnet，即如何将噪声从噪声-图像混合物中分离出来，从而将问题简化。
• 第二点，如果要预测一个正态分布，只需要学它的均值和方差即可，而DDPM将方差视作常数，只需学习均值就能得到分布，最后的效果也不错，并且降低了模型优化的难度

简单来说，一张图像哪怕加很多很多次标准高斯噪声，最后得到的纯标准高斯噪声中也包含少许的原始图像信息。也就是说，哪怕随便拿一个并非由图像加噪得到的真实高斯噪声出来，也可以视其为从某张真实世界并不存在的逼真图像加噪而来。如果能想办法推导出加的噪声是什么样的，那么自然就能完成去噪过程。但是这个"推导"目前无法由数学实现，只能通过训练网络来进行近似预测这个噪声。而且由于一步到位的去噪难度极高，因此要拆成很多步以便网络训练。需要注意的是，网络进行噪声预测并不是完全无依据的，而是去学会如何把噪声从噪声-图像混合物中给分离出来。

参考链接

1. The Annotated Diffusion Model
2. 带你深入理解扩散模型DDPM
3. 扩散模型全新课程：扩散模型从0到1实现！
4. Denoising Diffusion Probabilitistic Models
5. 《Diffusion Models Beat GANs on Image Synthesis》阅读笔记
6. How Diffusion Models Work
7. DDPM交叉熵损失函数推导
8. DDPM（Denoising Diffusion Probabilistic Models）扩散模型简述
9. What are Diffusion Models?
10. 由浅入深了解Diffusion Model
11. 什么是Diffusion模型？
12. Probabilistic Diffusion Model概率扩散模型理论与完整PyTorch代码详细解读
13. Denoising Diffusion Probabilistic Model, in Pytorch