可解释性重要性

机器学习模型在表现良好时，我们不能简单地信任其预测结果而忽略其决策原因。单一指标如分类准确率对现实世界任务来说是不完整的。因此，可解释性对于了解预测原因、模型的弱点以及修复系统非常重要。

可解释性的重要性包括满足人类的好奇心和学习需求，协调知识结构中元素之间的矛盾，检测模型的偏见，增加社会接受度，并用于管理社会互动。解释还有助于调试和审核机器学习模型，特别是在产品部署后出现问题时。通过解释决策，我们可以更轻松地检查公平性、隐私、鲁棒性、因果关系和信任等特征。

这种废话太多了，反正就是一句话可解释性好用，重要

可解释性事前与事后

可解释性分为事前（前置解释性）和事后（后置解释性）两种类型，它们分别强调了在构建模型之前和构建模型之后理解和解释模型的重要性。

1. 事前可解释性（前置解释性）：

事前可解释性指的是在构建机器学习模型之前，通过合理的模型选择、特征工程和设计等步骤，使模型更易于解释和理解。在这个阶段，我们采取一些措施来确保模型在构建过程中就具备较好的可解释性。这包括选择简单且易于解释的模型结构，使用人类可理解的特征，对特征进行预处理以减少冗余信息，以及遵循监管要求等。事前可解释性的优点是在模型构建阶段就能获得较好的解释性，使模型的决策过程更加透明和可信。

2. 事后可解释性（后置解释性）：

事后可解释性指的是在构建机器学习模型之后，通过解释方法和工具来分析已经构建好的模型，从而理解其内部决策过程和预测结果。在这个阶段，我们使用一些解释技术，如局部模型解释、特征重要性分析、影响力分析等，来帮助我们理解模型是如何做出预测的，哪些特征对预测结果产生了重要影响，以及模型的决策是否合理和可信。事后可解释性的优点是，即使我们在构建模型时没有考虑可解释性，通过后续的解释分析，仍然可以获得对模型的解释，从而增强对模型的理解和信任。

事前和事后可解释性相辅相成，都对于提高机器学习模型的可信度和可靠性至关重要。在构建模型时，我们可以通过合理的模型选择和特征工程来增强模型的可解释性。在模型构建完成后，我们可以使用解释技术来深入分析模型，理解其决策过程，发现潜在问题，并做出相应的优化和改进。综合两种解释性方法，我们可以更全面地了解和解释机器学习模型，从而使模型更具有可解释性和可信度。

可解释模型

线性回归

线性回归模型将目标变量预测为特征输入的加权和。学习到的线性关系使得解释容易。统计学家、计算机科学家以及其他处理定量问题的人长期以来一直使用线性模型。

线性模型可用于描述回归目标$y$在一些特征$x$上的依赖关系。对于单个实例$i$，学习到的关系可表示为：

$$y={\beta }_0+{\beta }_1{x}_1+...+{\beta }_p{x}_p+ϵ$$

实例的预测结果：其实是$p$个特征的加权和。参数${\beta }_j$表示学习到的特征权重或系数。总和中的第一个权重（${\beta }_0$）称为截距，不与特征相乘。$ϵ$是存在的误差，即预测值与实际结果之间的差异。这些误差假定遵循高斯分布，意味着在负向和正向都会出现误差，并且会出现许多小误差和少数大误差。

可以使用各种方法来估计最优权重。通常使用普通最小二乘法来找到最小化实际结果与预测结果之间差异的权重：

$$\hat{\beta }=argmi{n}_{{\beta }_0,...,{\beta }_p}\sum _{i=1}^n(y^{(i)}-({\beta }_0+\sum _{j=1}^p{\beta }_j{x}_j^{(j)}){)}^2$$

估计的权重附带置信区间。置信区间是对权重估计的范围，它以一定的置信度覆盖“真实”权重。例如，一个权重为2的95%置信区间可能从1到3。对于这个区间的解释是：如果使用新采样的数据重复100次估计，置信区间将在100次中的95次包含真实权重，前提是线性回归模型是正确的数据模型。

通过估计权重的置信区间，我们可以判断权重是否对于模型来说是显著的

另外可解释性线性模型的正确性取决于数据中的关系是否符合一些重要假设。这些假设包括：

1. 线性关系：可解释性线性模型假设因变量与自变量之间存在线性关系，即因变量的变化可以由自变量的线性组合来解释。如果数据中的关系是非线性的，线性模型可能无法准确捕捉数据的变化。
2. 正态性：线性模型假设残差（预测值与真实值之间的差异）是服从正态分布的。这个假设在许多统计推断和模型评估中都很重要。如果数据不符合正态分布，模型的推断和预测可能会受到影响。
3. 同方差性：线性模型假设残差的方差是恒定的，即在不同的自变量取值范围内，残差的方差应该保持不变。如果数据不符合同方差性假设，可能需要进行数据转换或使用其他类型的模型。
4. 独立性：线性模型假设观测之间是相互独立的，即一个观测的误差不会影响其他观测的误差。在时间序列数据或空间相关性较强的数据中，可能需要考虑违反独立性假设的情况。
5. 固定特征：线性模型假设自变量是固定的，即不随时间或其他条件的改变而变化。如果自变量是随时间变化的，可能需要考虑使用时间序列模型或其他动态模型。
6. 无多重共线性：线性模型假设自变量之间不存在高度相关性。多重共线性会导致估计的系数不稳定和模型的不确定性增加。

在应用可解释性线性模型时，必须认真检查数据是否满足这些假设。如果数据不符合这些假设，可能需要采取数据预处理或使用其他更适合数据特征的模型来获得更准确和可靠的结果。

可解释性

在线性回归模型中，权重的解释取决于相应特征的类型，线性回归模型中有如下特征：

• 数值特征： 将数值特征增加一个单位会使估计的结果变化其权重。一个数值特征的例子是房屋的大小。
• 二值特征： 每个实例都有两种可能值的特征。例如，特征“房屋带花园”。其中一种值被视为参考类别（在某些编程语言中编码为0），例如“没有花园”。将特征从参考类别更改为另一类别会使估计的结果变化其特征的权重。
• 具有多个类别的分类特征： 具有固定数量可能值的特征。例如，特征“地板类型”，具有可能的类别“地毯”、“层压板”和“实木地板”。处理多个类别的一种方法是一位有效编码，即每个类别都有自己的二值列。对于具有L个类别的分类特征，只需要L-1列，因为第L列会有冗余信息（例如，当实例的列1到L-1的所有值都为0时，我们知道该实例的分类特征为类别L）。然后，每个类别的解释与二值特征的解释相同。一些编程语言（例如R）允许您以各种方式对分类特征进行编码。
• 截距 (Intercept) ${\beta }_0$： 截距是“常数特征”的特征权重，对于所有实例始终为1。大多数软件包会自动添加这个“1”特征来估计截距。解释是：对于所有数值特征值为零，分类特征值为参考类别的实例，模型预测为截距权重。截距的解释通常不相关，因为所有特征值都为零的实例通常没有意义。只有在特征已标准化（均值为零，标准偏差为一）的情况下，解释才有意义。然后，截距反映了所有特征均为其均值的实例的预测结果。

线性回归模型中特征的解释可以通过以下文本模板自动化：

数值特征的解释

将特征$x_k$增加一个单位会使预测$y$增加${\beta }_k$单位，当所有其他特征值保持不变时。

分类特征的解释

将特征$x_k$从参考类别更改为另一类别会使预测$y$增加${\beta }_k$单位，当所有其他特征保持不变时。

线性模型解释的另一个重要指标是$R$平方（R-squared）。$R$平方告诉我们模型解释了目标变量总方差的多少。$R$平方越高，模型解释数据的能力越好。计算$R$平方的公式如下：

$$R^2=1-SSE/SST$$

其中$SSE$是误差项的平方和：
$$SSE=\sum _{i=1}^n(y^{(i)}-{\hat{y}}^{(i)}{)}^2$$

而$SST$是数据方差的平方和：

$$SST=\sum _{i=1}^n(y^{(i)}-\bar{y}{)}^2$$

$SSE$表示在拟合线性模型后剩余的方差，通过预测值和实际目标值之间的平方差来衡量。$SST$是目标变量的总方差。$R$平方告诉我们线性模型能够解释多少方差。$R$平方通常在 0 到 1 之间变化，其中 0 表示模型完全未解释数据，而 1 表示模型解释了数据的全部方差。R 平方也可以取负值而不违反任何数学规则。当$SSE$大于$SST$时会出现这种情况，这意味着模型未捕捉到数据的趋势，预测结果比使用目标的均值作为预测结果更差。

然而，有一个问题，因为$R$平方随着模型中特征数量的增加而增加，即使这些特征对目标值没有任何信息。因此，最好使用调整后的$R$平方，该指标考虑了模型中使用的特征数量。它的计算公式如下：

$${\bar{R}}^2=1-（1-R^2）\frac{n-1}{n-p-1}$$

其中$p$是特征数量，$n$是实例数量。

如果模型的（调整后的）$R$平方非常低，解释这样的模型就没有意义，因为这样的模型基本上无法解释大部分方差。任何关于权重的解释都不会有意义。

特征重要性

在线性回归模型中，特征的重要性可以通过其 $t$ 统计量的绝对值来衡量。$t$统计量是估计权重与其标准误差的比值。

$$t_{{\hat{\beta }}_j}=\frac{{\hat{\beta }}_j}{SE({\hat{\beta }}_j)}$$

来看看这个公式告诉我们什么：特征的重要性随着权重的增加而增加，这是有道理的。估计权重的方差越大（即我们对正确值越不确定），特征的重要性就越小，这也是有道理的。

example

在这个例子中，使用线性回归模型来预测特定一天租赁的自行车数量，考虑了天气和日历信息。为了进行解释，会检查估计的回归权重。特征包括数值特征和分类特征。对于每个特征，下表显示了估计的权重、估计的标准误差（$SE$）以及$t$统计量的绝对值（$|t|$）。

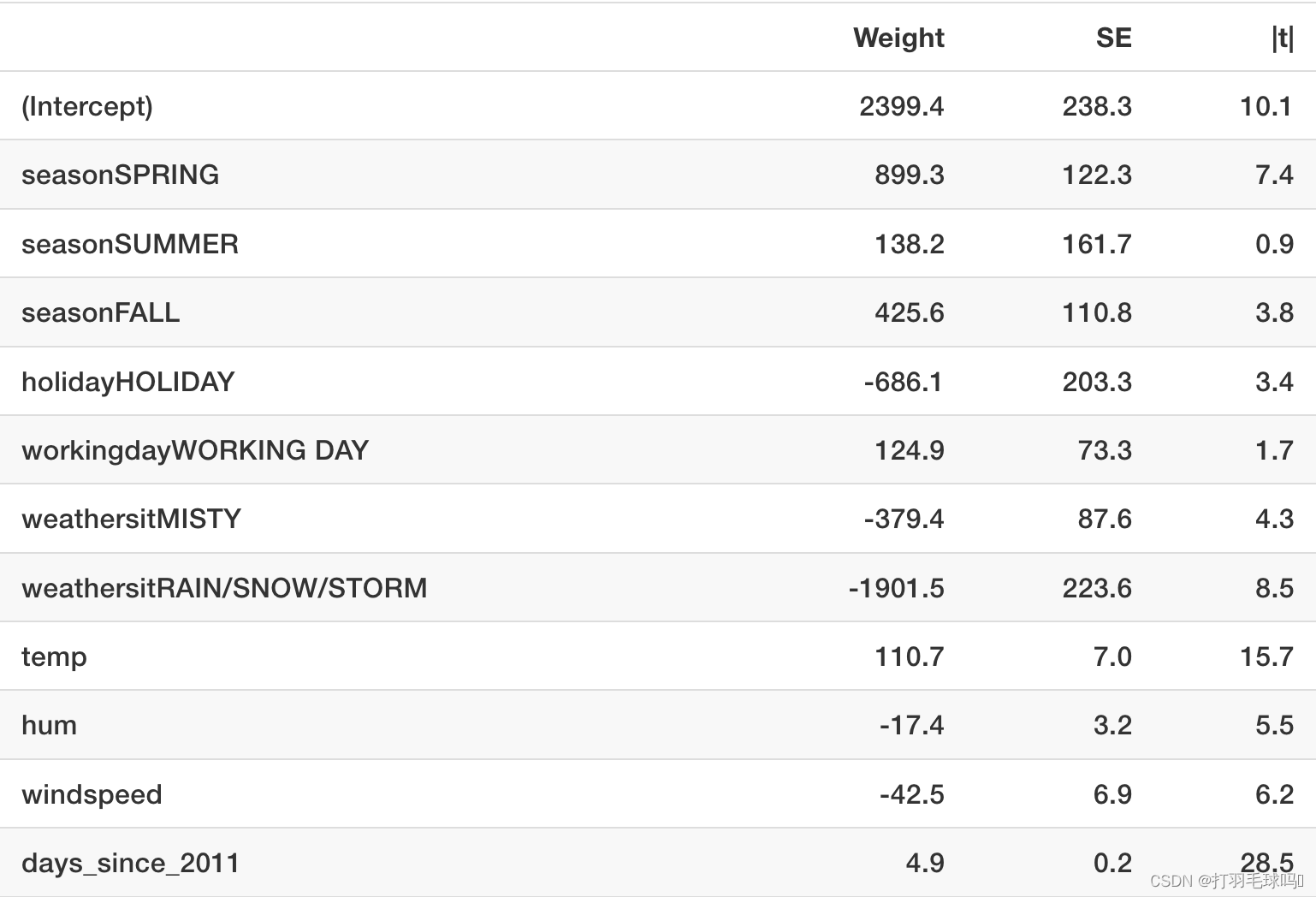
数值特征（温度）的解释：温度增加1摄氏度时，预测的自行车数量增加110.7，当其他所有特征保持不变时。

分类特征（“weathersit”）的解释：相比良好的天气，当天气是雨天、雪天或暴风天时，估计的自行车数量会减少1901.5。同样地，假设所有其他特征不变。当天气是雾天时，相比良好的天气，预测的自行车数量会减少379.4，前提是所有其他特征保持不变。

权重显著性判断

权重表中的信息（权重和方差估计）可以通过权重图进行可视化。下面的图显示了前面线性回归模型的结果。

权重图显示，雨天/雪天/暴风天的天气对预测的自行车数量有很强的负面影响。工作日特征的权重接近于零，并且零包含在95%的区间内，这意味着该特征的效应在统计上不显著。一些置信区间非常短，估计值接近于零，然而特征效应在统计上是显著的。温度就是其中一个候选特征。权重图的问题在于，这些特征以不同的尺度进行测量。虽然对于天气，估计的权重反映了良好天气和雨天/暴风雪天之间的差异，但对于温度，它只反映了1摄氏度的增加。您可以通过在拟合线性模型之前对特征进行缩放（零均值和标准偏差为一）来使估计的权重更具可比性。

逻辑回归

分类问题的一个解决方案是逻辑回归。逻辑回归模型不同于拟合一条直线或超平面，而是使用逻辑函数将线性方程的输出压缩在0和1之间。逻辑函数的定义如下：

$$logistic(\eta )=\frac{1}{1+exp(-\eta )}$$

从线性回归到逻辑回归的过渡相对直观。在线性回归模型中，我们通过线性方程来建模结果与特征之间的关系：

$${\hat{y}}^{(i)}={\beta }_0+{\beta }_1{x}_1^{(i)}+...+{\beta }_p{x}_p^{(i)}$$

而在分类问题中，更喜欢在0和1之间的概率值，因此需要将方程的右侧封装到逻辑函数中。这使得输出值仅限于0和1之间的取值。

$$P(y^{(i)}=1)=\frac{1}{1+exp(-({\beta }_0+{\beta }_1{x}_1^{(i)}+...+{\beta }_p{x}_p^{(i)}))}$$

可解释

逻辑回归中权重的解释与线性回归中的权重解释不同，因为逻辑回归中的结果是0到1之间的概率。权重不再线性地影响概率。加权总和通过逻辑函数转化为概率。因此，需要重新制定解释方程，使得公式的右侧只有线性项。

$$ln(\frac{P(y=1)}{1-P(y=1)})=log(\frac{P(y=1)}{P(y=0)})={\beta }_0+{\beta }_1{x}_1+...+{\beta }_p{x}_p$$

将 ln() 函数中的项称为“比率”（事件概率与非事件概率的比值），封装在对数中称为对数比率。

这个公式显示，逻辑回归模型是对数比率的线性模型。很好！但这听起来似乎不太有帮助！通过稍微调整一下这些项，您可以找出在改变特征 xj 时预测如何变化。为此，我们可以首先将 exp() 函数应用于方程的两边：

$$\frac{P(y=1)}{1-P(y=1)}=odds=exp({\beta }_0+{\beta }_1{x}_1+...+{\beta }_p{x}_p)$$

然后我们比较当我们将一个特征值增加1时会发生什么。但是与其关注差异，我们关注两个预测的比率：

$$\frac{odd{s}_{xj+1}}{oddsxj}=\frac{exp({\beta }_0+{\beta }_1{x}_1+...+{\beta }_j(x_j+1)+...+{\beta }_p{x}_p)}{exp({\beta }_0+{\beta }_1{x}_1+...+{\beta }_j(x_j)+...+{\beta }_p{x}_p)}$$

应用以下规则：

$$\frac{exp(a)}{exp(b)}=exp(a-b)$$

然后消除许多项：

$$\frac{odd{s}_{xj+1}}{oddsxj}=exp({\beta }_j(x_j+1)-{\beta }_j{x}_j)=exp({\beta }_j)$$

最后，得到了一个与特征权重的$exp()$函数相关的简单公式。特征增加一个单位会将比率（乘法）乘以$exp({\beta }_j)$的因子改变。也可以这样解释：特征 xj 增加一个单位会将对数比率增加相应权重的值。大多数人解释比率，因为思考某物的 ln() 已被认为对大脑来说较为困难。解释比率本身就需要一些适应。例如，如果您的比率为2，则意味着 y=1 的概率是 y=0 的两倍。如果您的权重（=对数比率）为0.7，则将相应特征增加一个单位会将比率乘以$exp(0.7)$（约为2），比率变为4。但通常您不会处理比率，而只将权重解释为比率。因为实际计算比率需要为每个特征设置一个值，只有在您想查看数据集的某个特定实例时才有意义。

这些是具有不同特征类型的逻辑回归模型的解释：

• 数值特征： 如果将特征$x_j$的值增加一个单位，估计的比率会变为 $exp({\beta }_j)$ 的倍数。
• 二元分类特征： 特征的两个值之一是参考类别（在某些语言中，编码为0的类别）。将特征$x_j$从参考类别更改为另一个类别会使估计的比率变为 $exp({\beta }_j)$ 的倍数。
• 具有多于两个类别的分类特征： 解决多个类别的一种方法是一位有效编码，意味着每个类别都有自己的列。对于具有 L 个类别的分类特征，您只需要 L-1 列，否则会过度参数化。第 L 个类别是参考类别。您可以使用任何线性回归中可用的其他编码。然后，每个类别的解释等同于二元特征的解释。
• 截距${\beta }_0$ ： 当所有数值特征为零，且分类特征为参考类别时，估计的比率为$exp({\beta }_0)$ 。解释截距权重通常是不相关的。

Example

使用逻辑回归模型基于一些风险因素来预测宫颈癌。下表显示了估计的权重、相关的比率（odds ratios）以及估计权重的标准误差。

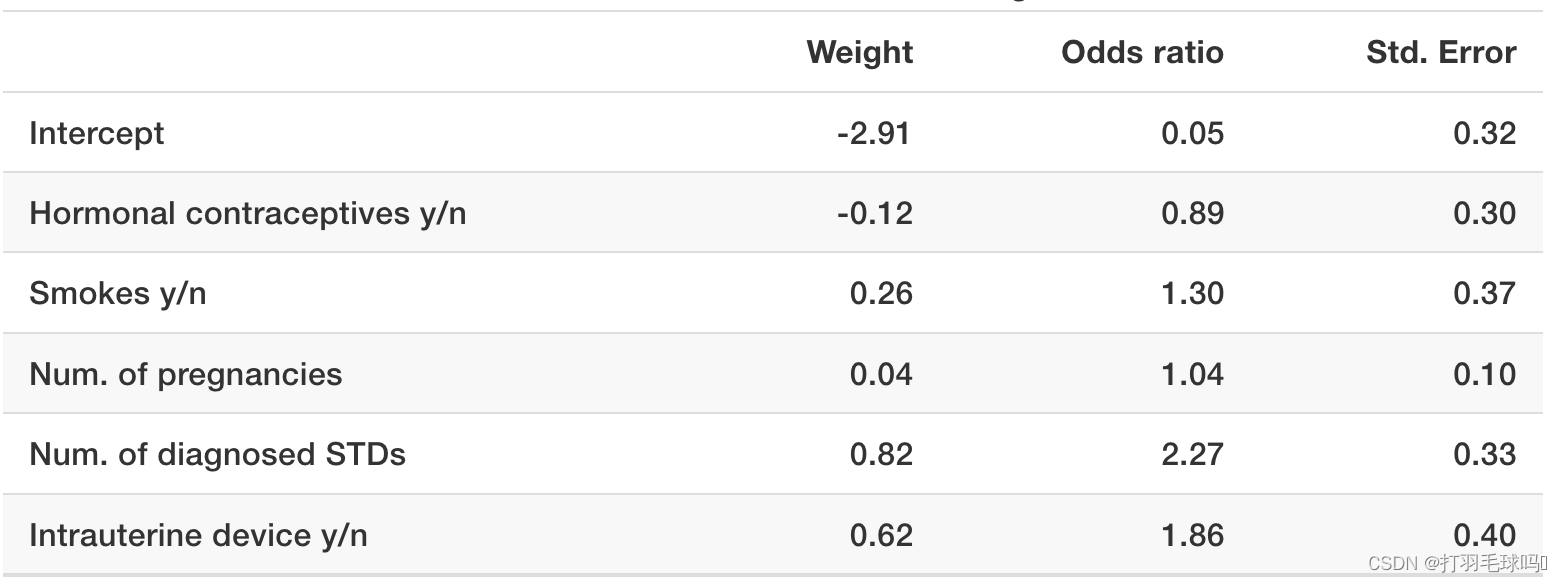
• 数值特征（“诊断的 STD 数量”）的解释： 诊断的性传播疾病（STDs）数量的增加会使癌症与无癌症的比率增加 2.27 倍，当所有其他特征保持不变时。请记住，相关性不意味着因果关系。
• 分类特征（“是否使用激素避孕药”）的解释： 对于使用激素避孕药的女性，相比于没有使用激素避孕药的女性，在所有其他特征保持不变的情况下，患癌症与无癌症之间的比率会减少 0.89 倍。

与线性模型类似，解释总是附带着“所有其他特征保持不变”的条件。