正文

　　大约在五六年前，第一次接触到了当时已经是hot topic的NoSql。不过那个时候学的用的都是mysql，Nosql对于我而言还是新事物，并没有真正使用，只是不明觉厉。但是印象深刻的是这么一张图片（后来google到图片来自这里）：

这张图片是讲数据库（包括传统的关系型数据库和NOSQL）与CAP理论的关系。由于并NoSql并没有实践经验，也没有去深入了解，对于CAP理论更是一知半解。因此，为什么某一款数据库被划分到哪一个阵营，并不清楚。

工作之后对MongoDB使用得比较多，有了一定的了解，前段时间又看到了这张图，于是想搞清楚，MongoDB是不是真的属于CP阵营，又是为什么？怀疑这个问题的初衷是因为，MongoDB的经典（官方推荐）部署架构中都会使用replica set，而replica set通过冗余和自动failover提供高可用性（Availability），那么为什么上图中说MongoDB牺牲了Avalability呢？而我在MongoDB的官方文档中搜索“CAP”，并没有搜索到任何内容。于是我想自己搞清楚这个疑问，给自己一个答案。

　　本文先阐明什么是CAP理论，以及关于CAP理论的一些文章，然后讨论MongoDB在一致性与可用性之间的折中与权衡。

CAP理论

对CAP理论我只知道这三个单词的意思，其解释也是来自网上的一些文章，并不一定准确。所以首先得追根溯源，搞清楚这个理论的起源和准确的解释。我觉得最好的开始就是wikipedia，从上面可以看到比较准确的介绍，更为重要的是可以看到很多有用的链接，比如CAP理论的出处，发展演变过程。

　　CAP理论是说对于分布式数据存储，最多只能同时满足一致性（C，Consistency）、可用性（A， Availability）、分区容错性（P，Partition Tolerance）中的两者。

　　一致性，是指对于每一次读操作，要么都能够读到最新写入的数据，要么错误。

　　可用性，是指对于每一次请求，都能够得到一个及时的、非错的响应，但是不保证请求的结果是基于最新写入的数据。

　　分区容错性，是指由于节点之间的网络问题，即使一些消息对包或者延迟，整个系统能继续提供服务（提供一致性或者可用性）。

　　一致性、可用性都是使用非常宽泛的术语，在不同的语义环境下具体所指是不一样的，比如在cap-twelve-years-later-how-the-rules-have-changed一文中Brewer就指出“CAP中的一致性与ACID中的一致性并不是同一个问题”，因此后文中除非特别说明，所提到的一致性、可用性都是指在CAP理论中的定义。只有明确了大家都是在同样的上下文环境，讨论才有意义。

　　对于分布式系统，网络分区（network partition）这种情况是难以避免的，节点间的数据复制一定存在延迟，如果需要保证一致性（对所有读请求都能够读到最新写入的数据），那么势必在一定时间内是不可用的（不能读取），即牺牲了可用性，反之亦然。

　　按照维基百科上的描述，CAP之间的相互关系大约起源于1998年，Brewer在2000年的PODC（Symposium on Principles of Distributed Computing）上展示了CAP猜想[3]，在2002年，由另外两名科学家Seth Gilbert、Nancy Lynch证明了Brewer的猜想，从而从猜想变成了定理[4]。

CAP理论起源

　　在Towards Robust Distributed Systems 中，CAP理论的提出者Brewer指出：在分布式系统中，计算是相对容易的，真正困难的是状态的维护。那么对于分布式存储或者说数据共享系统，数据的一致性保证也是比较困难的。对于传统的关系型数据库，优先考虑的是一致性而不是可用性，因此提出了事务的ACID特性。而对于许多分布式存储系统，则是更看重可用性而不是一致性，一致性通过BASE（Basically Available, Soft state, Eventual consistency）来保证。下面这张图展示了ACID与BASE的区别：

　　简而言之：BASE通过最终一致性来尽量保证服务的可用性。注意图中最后一句话“But I think it‘s a spectrum”，就是说ACID BASE只是一个度的问题，并不是对立的两个极端。

　　2002年，在Brewer's conjecture and the feasibility of consistent, available, partition-tolerant web services中，两位作者通过异步网络模型论证了CAP猜想，从而将Brewer的猜想升级成了理论（theorem）。但实话说，我也没有把文章读得很明白。

　　2009年的这篇文章brewers-cap-theorem，作者给出了一个比较简单的证明：

　　如上图所示，N1，N2两个节点存储同一份数据V，当前的状态是V0。在节点N1上运行的是安全可靠的写算法A，在节点N2运行的是同样可靠的读算法B，即N1节点负责写操作，N2节点负责读操作。N1节点写入的数据也会自动向N2同步，同步的消息称之为M。如果N1，N2之间出现分区，那么就没法保证消息M在一定的时间内到达N2。

　　从事务的角度来看这各问题

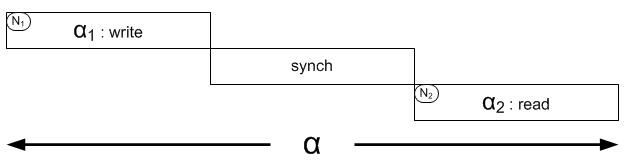
　　α这个事务由操作α1， α2组成，其中α1是写数据，α2是读数据。如果是单点，那么很容易保证α2能读到α1写入的数据。如果是分布式的情况的情况，除非能控制 α2的发生时间，否则无法保证 α2能读到 α1写入的数据，但任何的控制（比如阻塞，数据集中化等）要么破坏了分区容错性，要么损失了可用性。

　　另外，这边文章指出很多情况下 availability比consistency重要，比如对于facebook google这样的网站，短暂的不可用就会带来巨大的损失。

　　2010年的这篇文章brewers-cap-theorem-on-distributed-systems/，用了三个例子来阐述CAP，分别是example1：单点的mysql；example2：两个mysql，但不同的mysql存储不同的数据子集（类似sharding）；example3：两个mysql，对A的一个insert操作，需要在B上执行成功才认为操作完成（类似复制集）。作者认为在example1和example2上都能保证强一致性，但不能保证可用性；在example3这个例子，由于分区（partition）的存在，就需要在一致性与可用性之间权衡。

　　于我看来，讨论CAP理论最好是在“分布式存储系统”这个大前提下，可用性也不是说整体服务的可用性，而是分布式系统中某个子节点的可用性。因此感觉上文的例子并不是很恰当。

CAP理论发展

　到了2012年，CAP理论的发明人 Brewer就CAP理论再次撰文《CAP Twelve Years Later: How the "Rules" Have Changed》，这篇文章比较长，但思路清晰，高屋建瓴，非常值得一读。网上也有对用的中文译文《CAP理论十二年回顾："规则"变了》，翻译还不错。

　　文章中，最主要的观点是CAP理论并不是说三者不需选择两者。首先，虽然只要是分布式系统，就可能存在分区，但分区出现的概率是很小的（否则就需要去优化网络或者硬件），CAP在大多数时候允许完美的C和A；只有在分区存在的时间段内，才需要在C与A之间权衡。其次，一致性和可用性都是一个度的问题，不是0或者1的问题，可用性可以在0%到100%之间连续变化，一致性分为很多级别（比如在casandra，可以设置consistency level）。因此，当代CAP实践的目标应该是针对具体的应用，在合理范围内最大化数据一致性和可用性的效力。

　　文章中还指出，分区是一个相对的概念，当超过了预定的通信时限，即系统如果不能在时限内达成数据一致性，就意味着发生了分区的情况，必须就当前操作在C和A之间做出选择。

　　从收入目标以及合约规定来讲，系统可用性是首要目标，因而我们常规会使用缓存或者事后校核更新日志来优化系统的可用性。因此，当设计师选择可用性的时候，因为需要在分区结束后恢复被破坏的不变性约。

　　实践中，大部分团体认为（位于单一地点的）数据中心内部是没有分区的，因此在单一数据中心之内可以选择CA；CAP理论出现之前，系统都默认这样的设计思路，包括传统数据库在内。

　　分区期间，独立且能自我保证一致性的节点子集合可以继续执行操作，只是无法保证全局范围的不变性约束不受破坏。数据分片（sharding）就是这样的例子，设计师预先将数据划分到不同的分区节点，分区期间单个数据分片多半可以继续操作。相反，如果被分区的是内在关系密切的状态，或者有某些全局性的不变性约束非保持不可，那么最好的情况是只有分区一侧可以进行操作，最坏情况是操作完全不能进行。

　　上面摘录中下选线部分跟MongoDB的sharding情况就很相似，MongoDB的sharded cluste模式下，shard之间在正常情况下，是无需相互通信的。

　　在13年的文章中《better-explaining-cap-theorem》，作者指出“it is really just A vs C！”，因为

　　（1）可用性一般是在不同的机器之间通过数据的复制来实现

　　（2）一致性需要在允许读操作之间同时更新几个节点

　　（3）temporary partion，即几点之间的通信延迟是可能发生了，此时就需要在A 和 C之间权衡。但只有在发生分区的时候才需要考虑权衡。

　　在分布式系统中，网络分区一定会发生，因此“it is really just A vs C！”

MongoDB与CAP

在《通过一步步创建sharded cluster来认识MongoDB》一文中，对MongoDB的特性做了一些介绍，包括高性能、高可用、可扩展（水平伸缩），其中，MongoDB的高可用性依赖于replica set的复制与自动failover。对MongoDB数据库的使用有三种模式：standalone，replica set， shareded cluster，在前文中详细介绍了shared cluster的搭建过程。

　　standalone就是单个mongod，应用程序直接连接到这个Mongod，在这种情况下无分区容错性可言，也一定是强一致性的。对于sharded cluster，每一个shard也都推荐是一个replica set。MongoDB中的shards维护的是独立的数据子集，因此shards之间出现了分区影响不大（在chunk迁移的过程可能还是有影响），因此也主要考虑的是shard内部replica set的分区影响。所以，本文中讨论MongoDB的一致性、可用性问题，针对的也是MongoDB的replica set。

　　对于replica set，只有一个primary节点，接受写请求和读请求，其他的secondary节点接受读请求。这是一个单写、多读的情况，比多读、多写的情况还是简化了许多。后文为了讨论，也是假设replica set由三个基点组成，一个primary，两个secondary，且所有节点都持久化数据（data-bearing）

　　MongoDB关于一致性、可用性的权衡，取决于三者：write-concern、read-concern、read-preference。下面主要是MongoDB3.2版本的情况，因为read-concern是在MongoDB3.2版本中才引入的。

write-concern：

　　write concern表示对于写操作，MongoDB在什么情况下给予客户端响应。包括下面三个字段：

　　{ w: <value>, j: <boolean>, wtimeout: <number> }

　　w: 表示当写请求在value个MongoDB实例处理之后才向客户端返回。取值范围：

　　　　1：默认值，表示数据写入到standalone的MongoDB或者replica set的primary之后返回

　　　　0：不用写入就直接向客户端返回，性能高，但可能丢数据。不过可以配合j：True来增加数据的可持久性（durability）

　　　　>1: 只有在replica set环境下才有用，如果value大于的replica set中节点的数目，那么可能导致阻塞

　　　　‘majority’：当数据写入到replica set的大多数节点之后向客户端返回，对于这种情况，一般是配合read-concern使用：

　　　　After the write operation returns with a w: "majority" acknowledgement to the client, the client can read the result of that write with a "majority" readConcern

　　j：表示当写请求在写入journal之后才向客户端返回，默认为False。两点注意：

　　　　如果在对于未开启journaling的MongoDB实例使用j:True，会报错

　　　　在MongoDB3.2及之后，对于w>1, 需要所有实例都写到journal之后才返回

　　wtimeout：表示写入的超时时间，即在指定的时间（number），如果还不能向客户端返回（w大于1的情况），那么返回错误

　　　　默认为0，相当于没有设置该选项

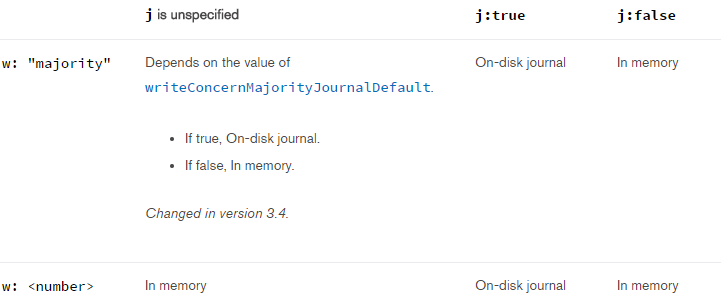
　　在MongoDB3.4中，加入了writeConcernMajorityJournalDefault.这么一个选项，使得w，j在不同的组合下情况下不同:

read-reference:

　　在前文已经讲解过，一个replica set由一个primary和多个secondary组成。primary接受写操作，因此数据一定是最新的，secondary通过oplog来同步写操作，因此数据有一定的延迟。对于时效性不是很敏感的查询业务，可以从secondary节点查询，以减轻集群的压力。

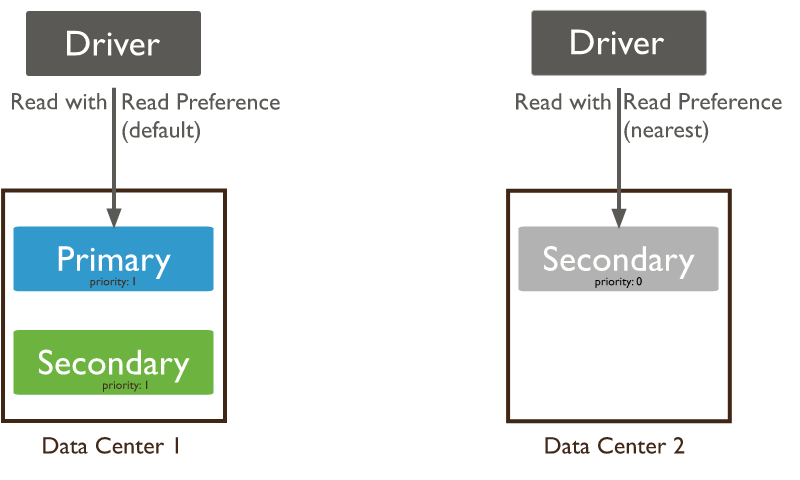
　　MongoDB指出在不同的情况下选用不同的read-reference，非常灵活。MongoDB driver支持一下几种read-reference：

　　primary：默认模式，一切读操作都路由到replica set的primary节点

　　primaryPreferred：正常情况下都是路由到primary节点，只有当primary节点不可用（failover）的时候，才路由到secondary节点。

　　secondary：一切读操作都路由到replica set的secondary节点

　　secondaryPreferred：正常情况下都是路由到secondary节点，只有当secondary节点不可用的时候，才路由到primary节点。

　　nearest：从延时最小的节点读取数据，不管是primary还是secondary。对于分布式应用且MongoDB是多数据中心部署，nearest能保证最好的data locality。

　　如果使用secondary或者secondaryPreferred，那么需要意识到：

　　(1) 因为延时，读取到的数据可能不是最新的，而且不同的secondary返回的数据还可能不一样；

　　(2) 对于默认开启了balancer的sharded collection，由于还未结束或者异常终止的chunk迁移，secondary返回的可能是有缺失或者多余的数据

　　(3) 在有多个secondary节点的情况下，选择哪一个secondary节点呢，简单来说是“closest”即平均延时最小的节点，具体参加Server Selection Algorithm

read-concern:

　　read concern是在MongoDB3.2中才加入的新特性，表示对于replica set（包括sharded cluster中使用复制集的shard）返回什么样的数据。不同的存储引擎对read-concern的支持情况也是不一样的

　　read concern有以下三个level：

　　local：默认值，返回当前节点的最新数据，当前节点取决于read reference。

　　majority：返回的是已经被确认写入到多数节点的最新数据。该选项的使用需要以下条件： WiredTiger存储引擎，且使用election protocol version 1；启动MongoDB实例的时候指定 --enableMajorityReadConcern选项。

　　linearizable：3.4版本中引入，这里略过了，感兴趣的读者参考文档。

　　在文章中有这么一句话：

Regardless of the read concern level, the most recent data on a node may not reflect the most recent version of the data in the system.

　　就是说，即便使用了read concern：majority，返回的也不一定是最新的数据，这个和NWR理论并不是一回事。究其根本原因，在于最终返回的数值只来源于一个MongoDB节点，该节点的选择取决于read reference。

　　在这篇文章中，对readconcern的引入的意义以及实现有详细介绍，在这里只引用核心部分：

readConcern 的初衷在于解决『脏读』的问题，比如用户从 MongoDB 的 primary 上读取了某一条数据，但这条数据并没有同步到大多数节点，然后 primary 就故障了，重新恢复后这个primary 节点会将未同步到大多数节点的数据回滚掉，导致用户读到了『脏数据』。

当指定 readConcern 级别为 majority 时，能保证用户读到的数据『已经写入到大多数节点』，而这样的数据肯定不会发生回滚，避免了脏读的问题。

一致性 or 可用性？

　　回顾一下CAP理论中对一致性可用性的问题：
　　一致性，是指对于每一次读操作，要么都能够读到最新写入的数据，要么错误。
　　可用性，是指对于每一次请求，都能够得到一个及时的、非错的响应，但是不保证请求的结果是基于最新写入的数据。

　　前面也提到，本文对一致性可用性的讨论是基于replica set的，是否是shared cluster并不影响。另外，讨论是基于单个客户端的情况，如果是多个客户端，似乎是隔离性的问题，不属于CAP理论范畴。基于对write concern、read concern、read reference的理解，我们可以得出以下结论。

默认情况（w：1、readconcern：local）如果read preference为primary，那么是可以读到最新的数据，强一致性；但如果此时primary故障，那么这个时候会返回错误，可用性得不到保证
默认情况（w：1、readconcern：local）如果read preference为secondary（secondaryPreferred、primaryPreferred），虽然可能读到过时的数据，但能够立刻得到数据，可用性比较好
writeconern：majority保证写入的数据不会被回滚; readconcern：majority保证读到的一定是不会被回滚的数据
若（w：1、readconcern；majority）即使是从primary读取，也不能保证一定返回最新的数据，因此是弱一致性
若（w: majority、readcocern：majority），如果是从primary读取，那么一定能读到最新的数据，且这个数据一定不会被回滚，但此时写可用性就差一些；如果是从secondary读取，不能保证读到最新的数据，弱一致性。

　　回过来来看，MongoDB所说的高可用性是更普世意义上的可用性：通过数据的复制和自动failover，即使发生物理故障，整个集群还是能够在短时间内回复，继续工作，何况恢复也是自动的。在这个意义上，确实是高可用的。