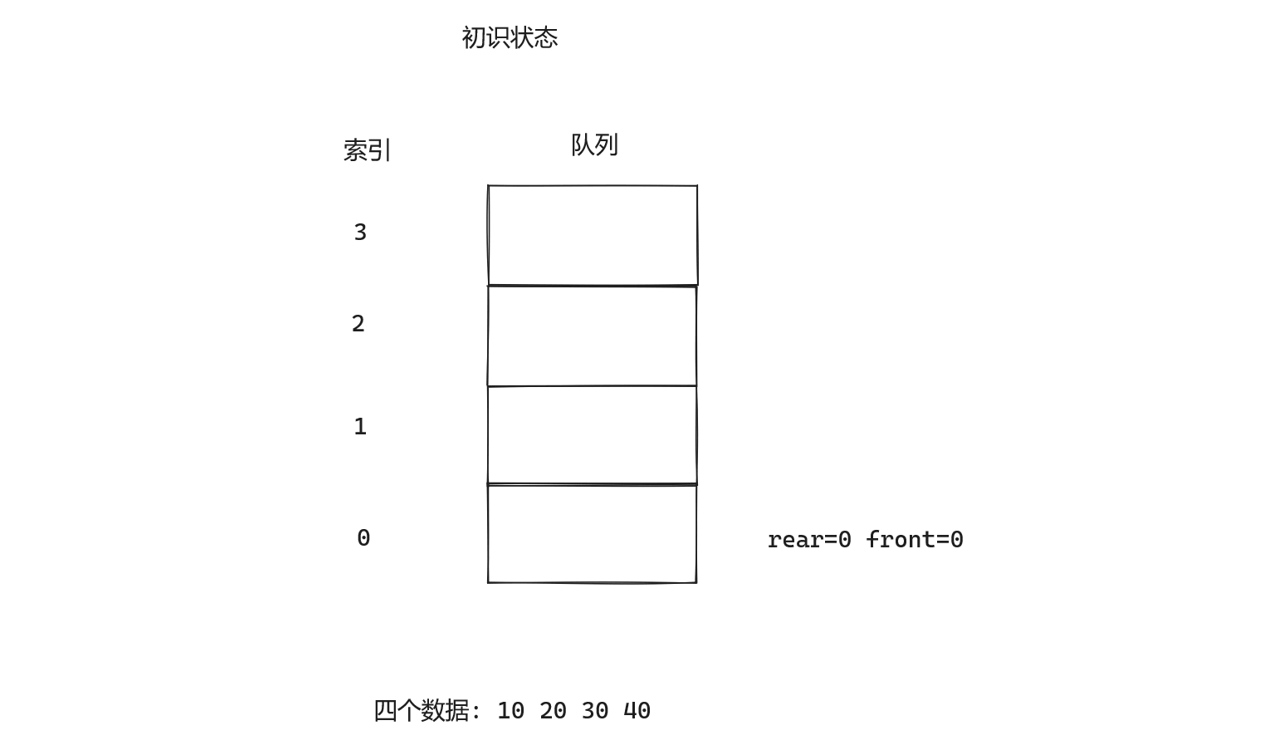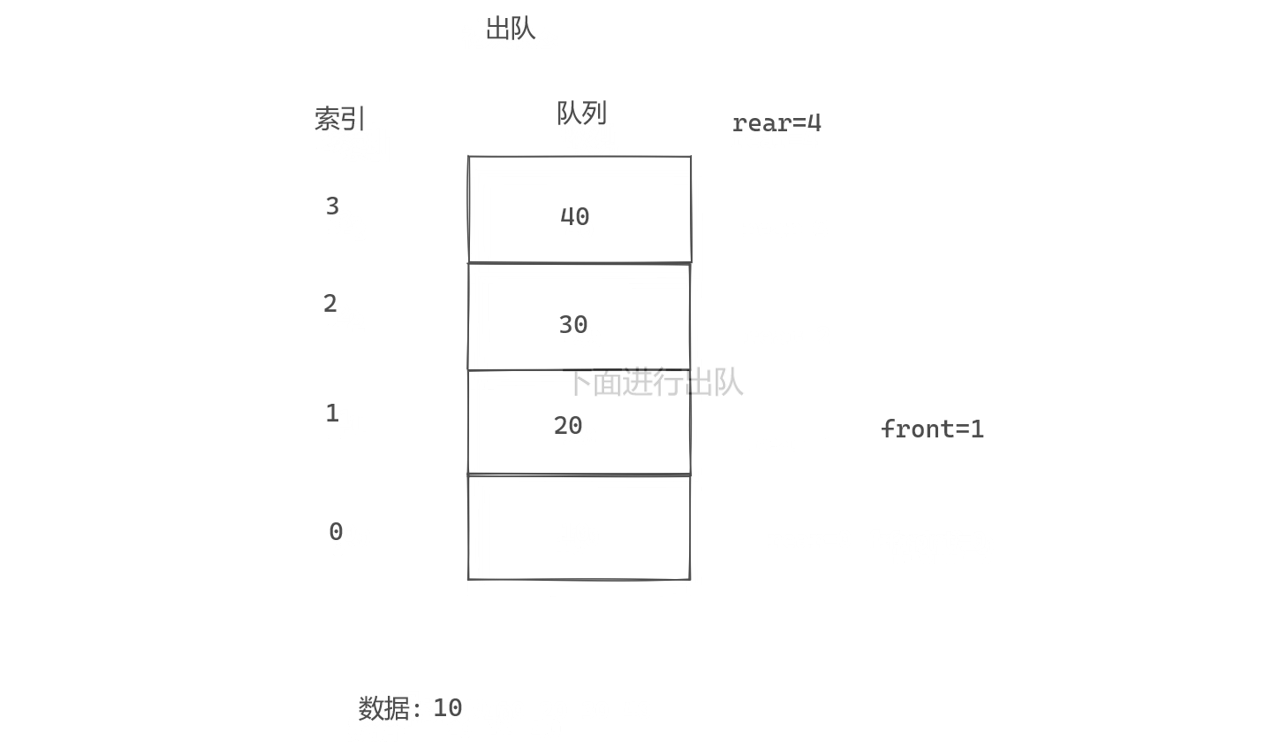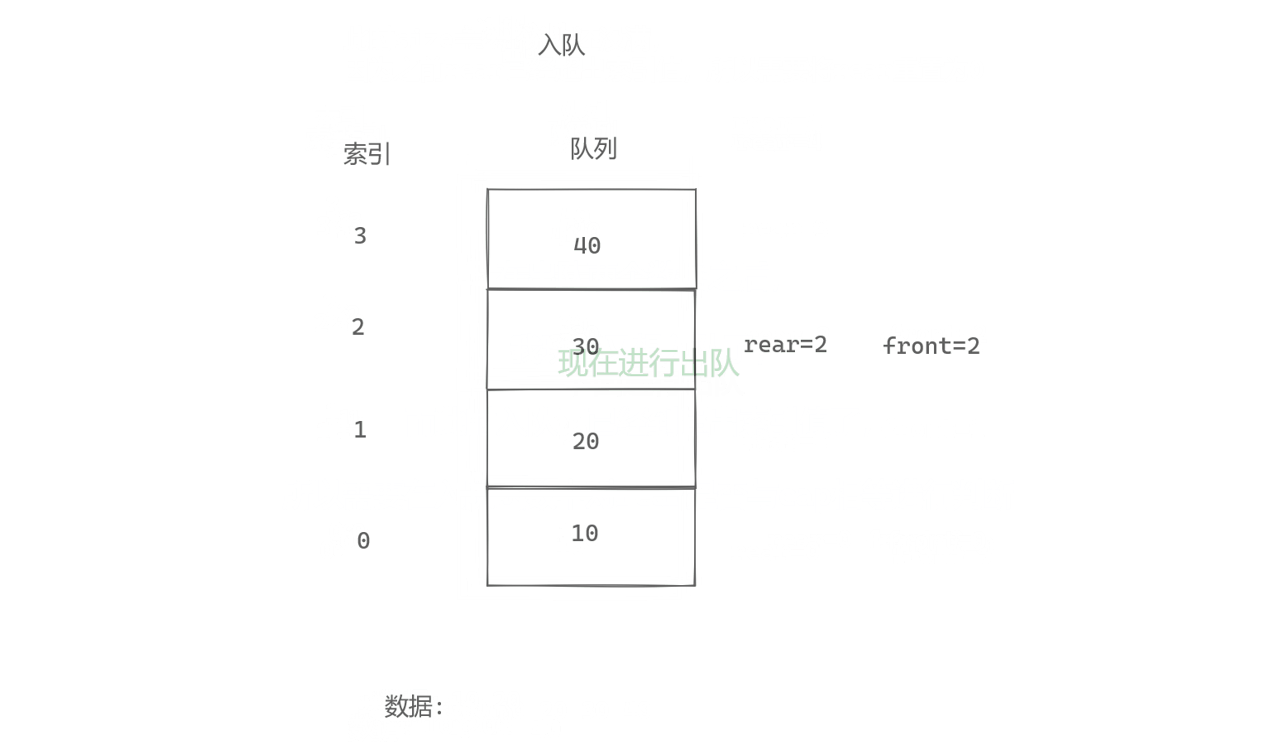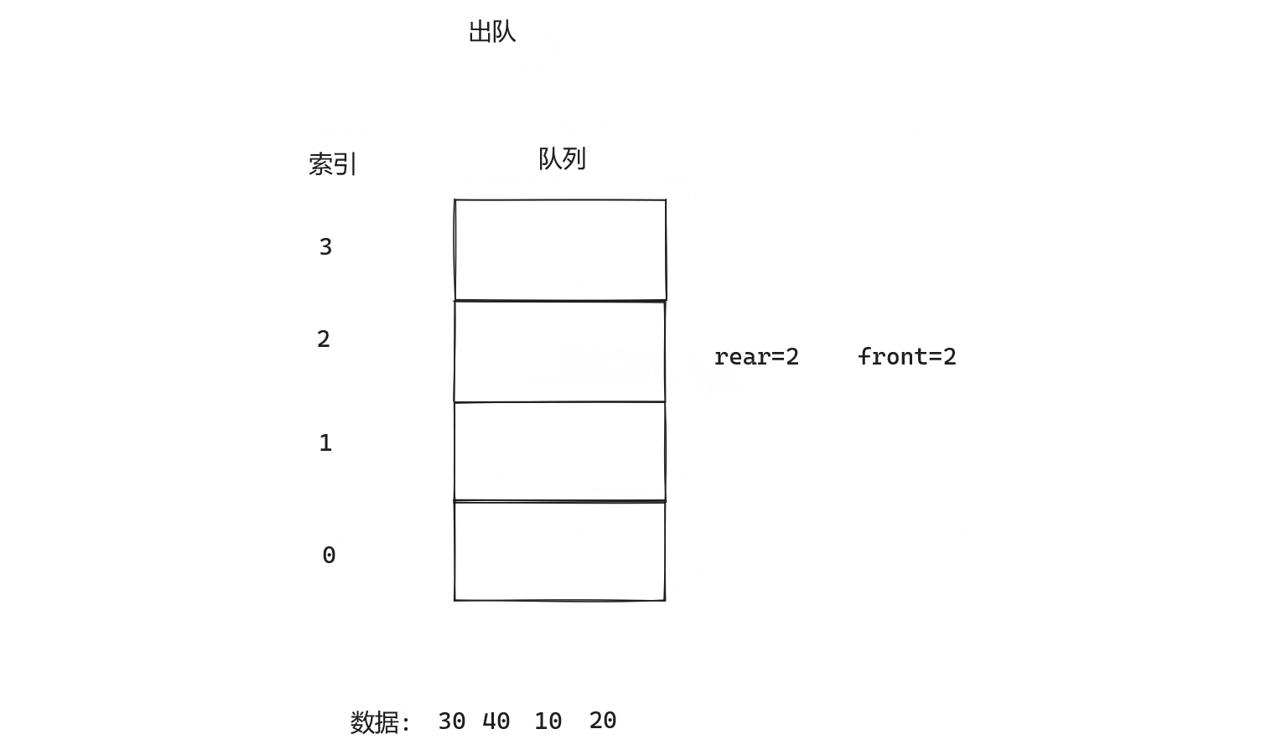
1.简述
一、符号微积分
- 微积分的数值计算方法只能求出以数值表示的近似解,而无法得到以函数形式表示的解析解。
- 在 MATLAB 中,可以通过符号运算获得微积分的解析解。
1. 符号极限
- MATLAB 中求函数极限的函数是
limit,可用来求函数在指定点的极限值和左右极限值。 - 对于极限值为没有定义的极限,MATLAB 给出的结果为 NaN,极限值为无穷大时,MATLAB 给出的结果为 Inf。
limit函数的调用格式如下。 - (1)
limit(f,x,a):求符号函数 f ( x ) f(x) f(x) 的极限值 lim x → a f ( x ) \lim_{x \to a}f(x) x→alimf(x) - 即计算当变量 x x x 趋近于常数 a a a 时, f ( x ) f(x) f(x) 函数的极限值。
- (2)
limit(f,a):求符号函数 f ( x ) f(x) f(x) 的极限值。由于没有指定符号函数 f ( x ) f(x) f(x)的自变量,则使用该格式时,符号函数 f ( x ) f(x) f(x) 的变量为函数symvar(f)确定的默认自变量,即变量 x x x 趋近于 ∞ \infty ∞。 - (3)
limit(f):求符号函数 f ( x ) f(x) f(x) 的极限值。符号函数 f ( x ) f(x) f(x) 的变量为函数symvar(f)确定的默认变量;没有指定变量的目标值时,系统默认变量趋近于 0,即 a = 0 a=0 a=0 的情况。 - (4)
limit(f,x,a,'right'):求符号函数 f ( x ) f(x) f(x) 的极限值 lim x → a + \lim_{x \to a^{+} } x→a+lim - ‘right’ 表示变量 x x x 从右边趋近于 a a a。
- (5)
limit(f;x,a,'lef'):求符号函数 f ( x ) f(x) f(x) 的极限值 lim x → a − \lim_{x \to a^{-} } x→a−lim - ‘left’ 表示变量 x x x 从左边趋近于 a a a。
2.代码及运行结果
%% 学习目标:matlab符号微积分和极限、
%% 微分
clear all;
syms x y;
f=5*x^4+y*sin(x)+x*cos(y)+6
g1=diff(f)
g2=diff(f,3) %求3阶导数
g3=diff(f,x,3)
g4=diff(f,y,3)

%% 极限
clear all;
syms x h;
y1=limit((cos(x+h)-cos(x))/h,h,0) %相当于求导cos x
y2=limit(((x+h)^3-x^3)/h,h,0)

%%
%% 不定积分
clear all;
syms x y;
f1=cos(x)+cos(y)
g1=int(f1)
g2=int(f1,x)
g3=int(f1,y)

%% 定积分
clear all;
syms x;
f1=1/x^2+sin(x)
g1=int(f1,1,3)
g2=int(f1,x,1,3)
f2=3/x^2;
g3=int(f2,x,1,+inf)