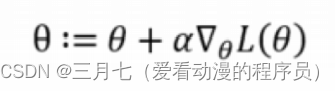概率图模型(Probabilistic Graphical Model,PGM),是一种用图结构来描述多元随机变量之间条件独立性的概率模型。它可以用来表示复杂的概率分布,进行有效的推理和学习,以及解决各种实际问题,如图像处理,自然语言处理,生物信息学,社会网络分析等。
概率图模型有两大类:有向图模型和无向图模型。有向图模型使用有向非循环图(Directed Acyclic Graph,DAG)来表示变量之间的因果关系,也称为贝叶斯网络(Bayesian Network)或信念网络(Belief Network)。无向图模型使用无向图(Undirected Graph)来表示变量之间的相关关系,也称为马尔可夫网络(Markov Network)或马尔可夫随机场(Markov Random Field)。
概率图模型的基本问题有三个:表示、推断和学习。表示问题是指如何用图结构和参数来定义一个概率分布。推断问题是指如何根据已知的观测变量和参数,计算未知的隐变量或者边缘概率。学习问题是指如何根据已知的观测数据,估计未知的参数或者图结构。
为了让你更清楚地理解概率图模型的含义,我为你准备了以下的例子:
假设你有一个朋友圈,其中有五个人:Alice, Bob, Carol, David和Eve。你想要知道他们之间的友谊关系,以及他们的喜好和性格。你可以用一个概率图模型来表示这个问题,如下图所示:
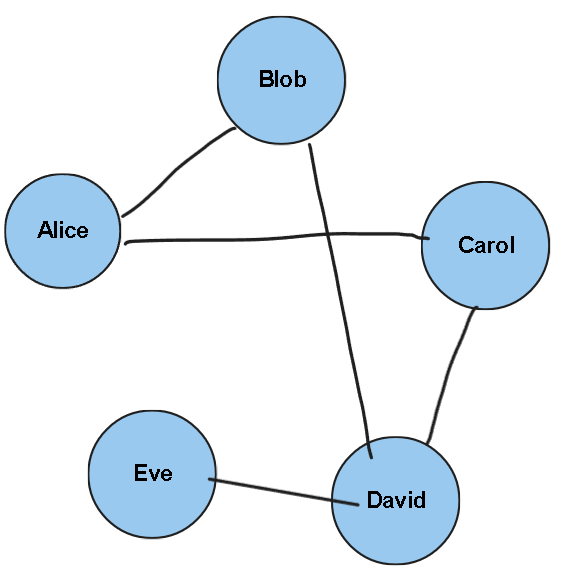
这个图中,每个节点代表一个人,每个节点有两个属性:爱好(hobby)和性格(personality)。每条边代表两个人之间是否是朋友。这个图就是一个无向图模型的例子,它可以用来表示五个人的爱好和性格的联合概率分布,以及他们之间的友谊关系。


这个公式的含义是:五个人的爱好和性格的联合概率分布等于所有可能的组合乘以相应的势函数再除以归一化常数。势函数可以看作是一种度量变量之间相关程度的函数,它越大,说明变量之间越相关;它越小,说明变量之间越独立。