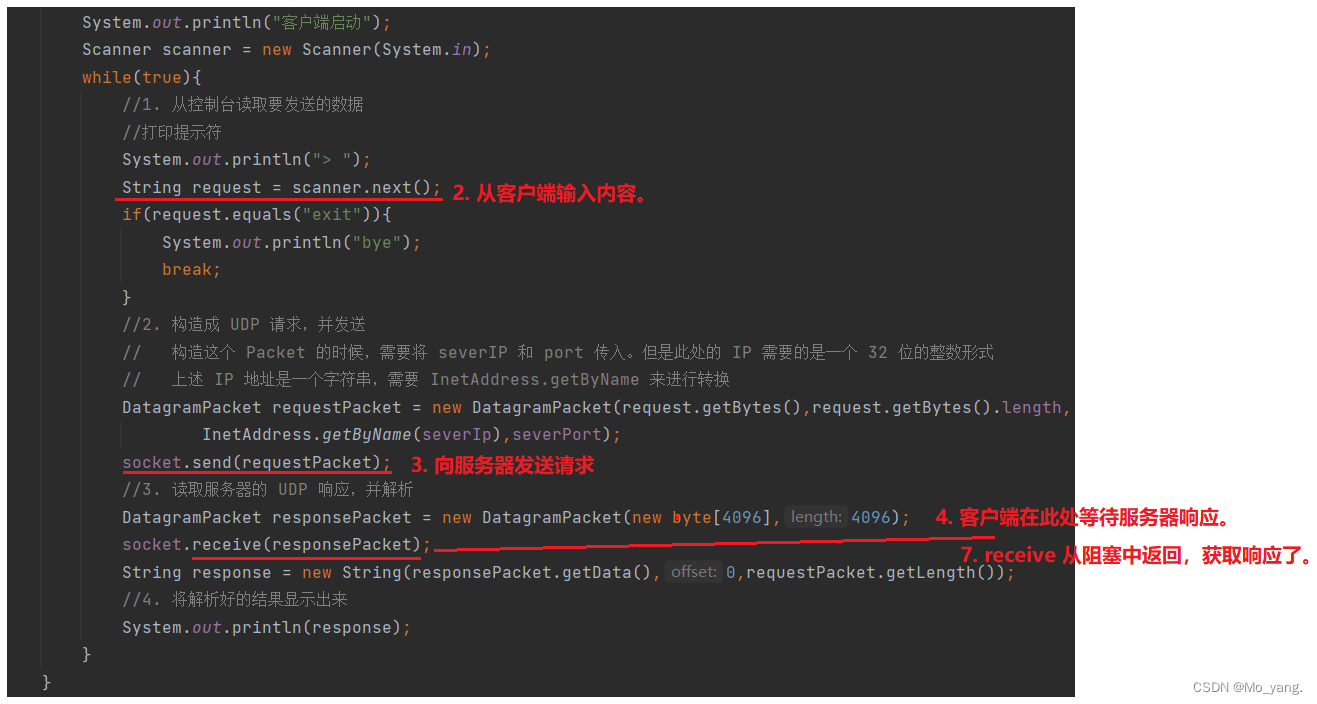
一、说明

老实说，我厌倦了几乎每天都在社交媒体和我的大学里听到这场辩论。通常，这伴随着一些模糊的陈述来解释这个问题。双方都为此感到内疚。我希望在本文结束时，您将对这些有些模糊的术语有更明智的立场。

二、论点

与普遍的看法相反，机器学习已经存在了几十年。它最初因其巨大的计算需求和当时存在的计算能力的限制而被回避。然而，由于信息爆炸产生的数据占主导地位，机器学习近年来出现了复兴。

那么，如果机器学习和统计学是同义词，为什么我们没有看到每所大学的统计系都关闭或过渡到“机器学习”系呢？因为它们不一样！

关于这个话题，我经常听到几个模糊的说法，最常见的是这样的：

“机器学习和统计学之间的主要区别在于它们的目的。机器学习模型旨在实现最准确的预测。统计模型是为推断变量之间的关系而设计的。

虽然这在技术上是正确的，但它并没有给出特别明确或令人满意的答案。机器学习和统计学之间的主要区别确实是它们的目的。然而，说机器学习是关于准确的预测，而统计模型是为推理而设计的，这几乎是一个毫无意义的陈述，除非你精通这些概念。

首先，我们必须了解统计和统计模型是不一样的。统计学是对数据的数学研究。除非你有数据，否则无法进行统计。统计模型是数据的模型，用于推断数据中的某些关系或创建能够预测未来值的模型。通常，这两者是齐头并进的。

因此，我们实际上需要讨论两件事：首先，统计与机器学习有何不同，其次，统计模型与机器学习有何不同。

为了使这一点更加明确，有许多统计模型可以进行预测，但预测准确性不是它们的强项。

同样，机器学习模型提供了不同程度的可解释性，从高度可解释的套索回归到难以理解的神经网络，但它们通常会为了预测能力而牺牲可解释性。

从高层次的角度来看，这是一个很好的答案。对于大多数人来说已经足够了。然而，在某些情况下，这种解释会让我们对机器学习和统计建模之间的差异产生误解。让我们看一下线性回归的例子。

三、统计模型与机器学习 — 线性回归示例

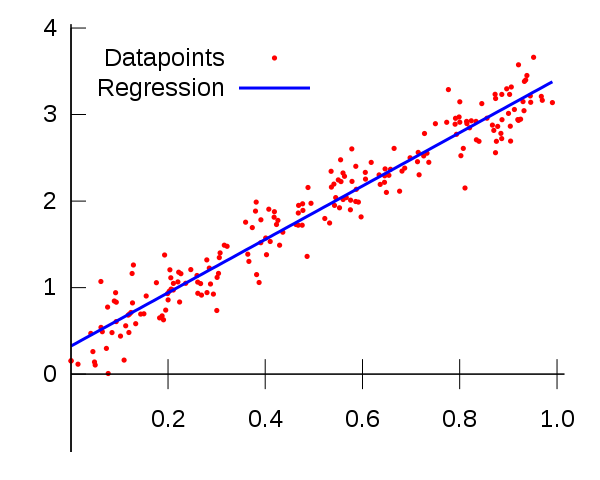
在我看来，统计建模和机器学习中使用的方法的相似性使人们认为它们是同一件事。这是可以理解的，但根本不是真的。

最明显的例子是线性回归的情况，这可能是造成这种误解的主要原因。线性回归是一种统计方法，我们可以训练线性回归器并获得与统计回归模型相同的结果，旨在最小化数据点之间的平方误差。

我们看到，在一种情况下，我们执行了称为“训练”模型的操作，这涉及使用数据子集，并且我们不知道模型的性能如何，直到我们在训练期间不存在的其他数据（称为测试集）上“测试”这些数据。在这种情况下，机器学习的目的是在测试集上获得最佳性能。

对于统计模型，我们找到一条线，该线最小化所有数据的均方误差，假设数据是添加了一些随机噪声的线性回归量，这通常是高斯的。无需培训，也无需测试集。在许多情况下，特别是在研究中（例如下面的传感器示例），我们模型的重点是表征数据和结果变量之间的关系，而不是对未来数据进行预测。我们称此过程为统计推断，而不是预测。但是，我们仍然可以使用此模型进行预测，这可能是您的主要目的，但评估模型的方式将不涉及测试集，而是涉及评估模型参数的重要性和鲁棒性。

（监督）机器学习的目的是获得一个可以做出可重复预测的模型。我们通常不在乎模型是否可解释，尽管我个人建议始终进行测试以确保模型预测确实有意义。机器学习是关于结果的，它可能在一家公司工作，你的价值完全取决于你的表现。然而，统计建模更多的是关于发现变量之间的关系以及这些关系的重要性，同时也迎合预测。

为了具体举例说明这两个程序之间的区别，我将举一个个人的例子。白天，我是一名环境科学家，主要处理传感器数据。如果我试图证明传感器能够响应某种刺激（例如气体浓度），那么我会使用统计模型来确定信号响应是否具有统计意义。我会尝试理解这种关系并测试其可重复性，以便我可以准确地表征传感器响应并根据这些数据进行推断。我可能会测试一些事情是响应是否实际上是线性的，响应是否可以归因于气体浓度而不是传感器中的随机噪声等。

相比之下，我还可以得到一个由20个不同传感器组成的阵列，我可以用它来尝试预测我新表征的传感器的响应。如果您对传感器了解不多，这可能看起来有点奇怪，但这目前是环境科学的一个重要领域。一个有20个不同变量的模型来预测我的传感器的结果，显然是关于预测的，我并不期望它特别可解释。由于化学动力学以及物理变量与气体浓度之间的关系产生的非线性，该模型可能会像神经网络一样更深奥。我希望这个模型有意义，但只要我能做出准确的预测，我就会很高兴。

如果我试图证明我的数据变量之间的关系具有一定程度的统计意义，以便我可以将其发表在科学论文中，我会使用统计模型而不是机器学习。这是因为我更关心变量之间的关系，而不是做出预测。做出预测可能仍然很重要，但大多数机器学习算法缺乏可解释性，因此很难证明数据中的关系（这实际上是现在学术研究中的一个大问题，研究人员使用他们不理解的算法并获得似是而非的推论）。

来源：分析维迪亚

应该明确的是，这两种方法的目标不同，尽管使用类似的手段来实现目标。机器学习算法的评估使用测试集来验证其准确性。然而，对于统计模型，通过置信区间、显著性检验和其他检验对回归参数的分析可用于评估模型的合法性。由于这些方法产生相同的结果，因此很容易理解为什么人们会假设它们是相同的。

四、统计与机器学习 — 线性回归示例

我认为这种误解很好地概括在这个表面上诙谐的10年挑战中，比较统计学和机器学习。

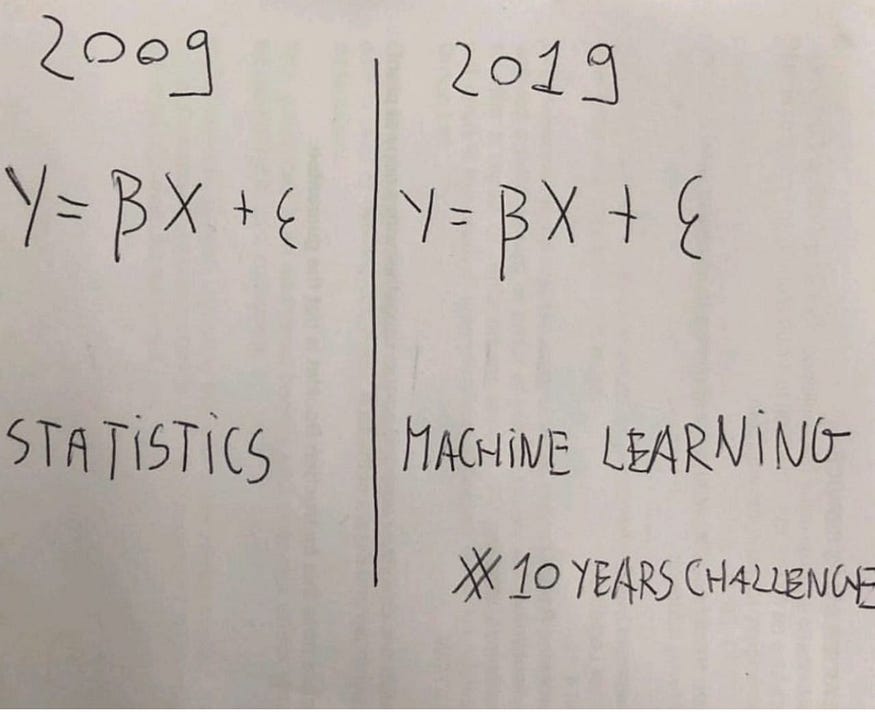
然而，仅仅基于这两个术语都利用了相同的基本概率概念这一事实而将这两个术语混为一谈是不合理的。例如，如果我们声明机器学习只是基于这一事实的美化统计数据，我们也可以做出以下声明。

物理学只是美化的数学。

动物学只是美化的邮票收藏。

建筑只是美化的沙堡建筑。

这些陈述（尤其是最后一个）非常荒谬，并且都基于将建立在类似想法上的术语混为一谈的想法（用于体系结构示例的双关语）。

实际上，物理学是建立在数学之上的，它是应用数学来理解现实中存在的物理现象。物理学还包括统计学的各个方面，现代形式的统计学通常是从由Zermelo-Frankel集合论与测度论相结合以产生概率空间的框架构建的。它们都有很多共同点，因为它们来自相似的起源，并应用相似的想法来得出合乎逻辑的结论。同样，建筑和沙堡建筑可能有很多共同点——虽然我不是建筑师，所以我不能给出一个明智的解释——但它们显然是不一样的。

为了让你了解这场辩论的范围，实际上有一篇发表在《自然方法》上的论文概述了统计学和机器学习之间的区别。这个想法可能看起来很可笑，但这种程度的讨论是必要的，这有点可悲。

在我们继续之前，我将快速澄清与机器学习和统计学相关的另外两个常见误解。这些是人工智能不同于机器学习，数据科学不同于统计学。这些都是相当无可争议的问题，所以它会很快。

数据科学本质上是应用于数据的计算和统计方法，这些可以是小型或大型数据集。这还可以包括探索性数据分析之类的东西，其中数据被检查和可视化，以帮助科学家更好地理解数据并从中做出推断。数据科学还包括数据整理和预处理等内容，因此涉及一定程度的计算机科学，因为它涉及编码，在数据库，Web服务器等之间建立连接和管道。

你不一定需要使用计算机来做统计，但如果没有计算机，你就无法真正做数据科学。你可以再次看到，虽然数据科学使用统计学，但它们显然是不一样的。

同样，机器学习与人工智能也不相同。事实上，机器学习是人工智能的一个子集。这是非常明显的，因为我们正在教（“训练”）一台机器，以根据以前的数据对某种类型的数据进行可概括的推断。

五、机器学习建立在统计学之上

在我们讨论统计学和机器学习的不同之处之前，让我们先讨论一下相似之处。我们已经在前面的部分中谈到了这一点。

机器学习建立在统计框架之上。这应该是显而易见的，因为机器学习涉及数据，并且必须使用统计框架来描述数据。然而，统计力学扩展到大量粒子的热力学，也是建立在统计框架之上的。压力的概念其实是一个统计，温度也是一个统计。如果你认为这听起来很荒谬，很公平，但这实际上是真的。这就是为什么你不能描述分子的温度或压力，这是荒谬的。温度是分子碰撞产生的平均能量的表现形式。对于足够多的分子，我们可以描述房屋或户外的温度是有意义的。

你会承认热力学和统计学是一样的吗？不，热力学使用统计学来帮助我们以传递现象的形式理解功和热的相互作用。

事实上，除了统计学之外，热力学是建立在更多项目之上的。同样，机器学习借鉴了数学和计算机科学的大量其他领域，例如：

数学和统计学等领域的ML理论
来自优化、矩阵代数、微积分等领域的 ML 算法
计算机科学与工程概念的ML实现（例如内核技巧，特征散列）

当一个人开始在Python上编码并开发sklearn库并开始使用这些算法时，很多这些概念都被抽象出来，因此很难看到这些差异。在这种情况下，这种抽象导致了对机器学习实际涉及的内容的无知。

六、统计学习理论——机器学习的统计基础

统计学和机器学习之间的主要区别在于统计学完全基于概率空间。你可以从集合论中推导出整个统计量，它讨论了我们如何将数字分组到称为集合的类别中，然后对该集合施加一个度量，以确保所有这些的总和值为 1。我们称之为概率空间。

统计学除了这些集合和度量的概念之外，没有对宇宙做出其他假设。这就是为什么当我们用非常严格的数学术语指定概率空间时，我们指定了 3 件事。

我们这样表示的概率空间（Ω，F，P）由三部分组成：

样本空间 Ω，它是所有可能结果的集合。
一组事件 F，其中每个事件都是包含零个或多个结果的集合。
事件概率的分配，P;也就是说，从事件到概率的函数。

机器学习基于统计学习理论，该理论仍然基于概率空间的公理化概念。该理论是在1960年代发展起来的，并在传统统计学的基础上进行了扩展。

机器学习有几类，因此我在这里只关注监督学习，因为它是最容易解释的（尽管它仍然有些深奥，因为它被埋在数学中）。

监督学习的统计学习理论告诉我们，我们有一组数据，我们将其表示为 S = {（xi，yi）}。这基本上是说我们是一个由n个数据点组成的数据集，每个数据点都由一些我们称之为特征的其他值描述，这些值由x提供，这些特征由某个函数映射，给我们值y。

它说我们知道我们有这些数据，我们的目标是找到将 x 值映射到 y 值的函数。我们将所有可能的函数的集合称为假设空间，这些函数可以将此映射描述为假设空间。

为了找到这个函数，我们必须给算法一些方法来“学习”解决问题的最佳方法。这是由称为损失函数的东西提供的。因此，对于我们拥有的每个假设（提议的函数），我们需要通过查看其对所有数据的预期风险值来评估该函数的性能。

预期风险本质上是损失函数乘以数据概率分布的总和。如果我们知道映射的联合概率分布，就很容易找到最佳函数。然而，这通常是未知的，因此我们最好的选择是猜测最佳函数，然后凭经验决定损失函数是否更好。我们称之为经验风险。

然后，我们可以比较不同的函数并寻找为我们提供最小预期风险的假设，即给出数据上所有假设的最小值（称为下确值）的假设。

但是，该算法倾向于作弊，以便通过过度拟合数据来最小化其损失函数。这就是为什么在基于训练集数据学习函数后，该函数会在测试数据集上验证，这些数据没有出现在训练集中。

我们刚刚定义机器学习的本质引入了过度拟合的问题，并证明了在执行机器学习时需要训练和测试集的合理性。这不是统计学的固有特征，因为我们并没有试图将经验风险降至最低。

选择最小化经验风险的函数的学习算法称为经验风险最小化。

七、例子

以线性回归的简单情况为例。在传统意义上，我们试图最小化某些数据之间的误差，以便找到可用于描述数据的函数。在这种情况下，我们通常使用均方误差。我们将其平方，以便正误差和负误差不会相互抵消。然后，我们可以以封闭形式求解回归系数。

碰巧的是，如果我们把损失函数作为均方误差，并按照统计学习理论的支持执行经验风险最小化，我们最终会得到与传统线性回归分析相同的结果。

这只是因为这两种情况是等效的，就像对相同的数据执行最大似然也会给你相同的结果一样。最大似然有不同的方式来实现相同的目标，但没有人会争论并说最大似然与线性回归相同。最简单的情况显然无助于区分这些方法。

这里要强调的另一点是，在传统的统计方法中，没有训练和测试集的概念，但我们确实使用指标来帮助我们检查模型的性能。因此，评估程序是不同的，但两种方法都能够为我们提供统计上稳健的结果。

还有一点是，这里的传统统计方法给了我们最优解，因为解有一个封闭的形式。它没有测试任何其他假设并收敛到解决方案。然而，机器学习方法尝试了一堆不同的模型，并收敛到最终的假设，这与回归算法的结果一致。

如果我们使用不同的损失函数，结果就不会收敛。例如，如果我们使用铰链损失（使用标准梯度下降无法区分，因此需要其他技术，如近端梯度下降），那么结果将不相同。

最终的比较可以通过考虑模型的偏差来进行。人们可以要求机器学习算法测试线性模型，以及多项式模型、指数模型等，看看这些假设是否更适合给定我们的先验损失函数的数据。这类似于增加相关的假设空间。在传统的统计意义上，我们选择一个模型并可以评估其准确性，但不能自动使其从 100 个不同的模型中选择最佳模型。显然，模型中总是存在一些偏差，这源于算法的初始选择。这是必要的，因为找到最适合数据集的任意函数是一个 NP-hard 问题。