1.题目

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

• 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
• 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
• 如果这个过程 结果为 1，那么这个数就是快乐数。

如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

2.示例

示例 1：

输入：n = 19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

示例 2：

输入：n = 2
输出：false

---

3.思路

快慢指针法
         如果观察规律可以发现如果不是快乐数则会一直陷入一个循环之中。如图

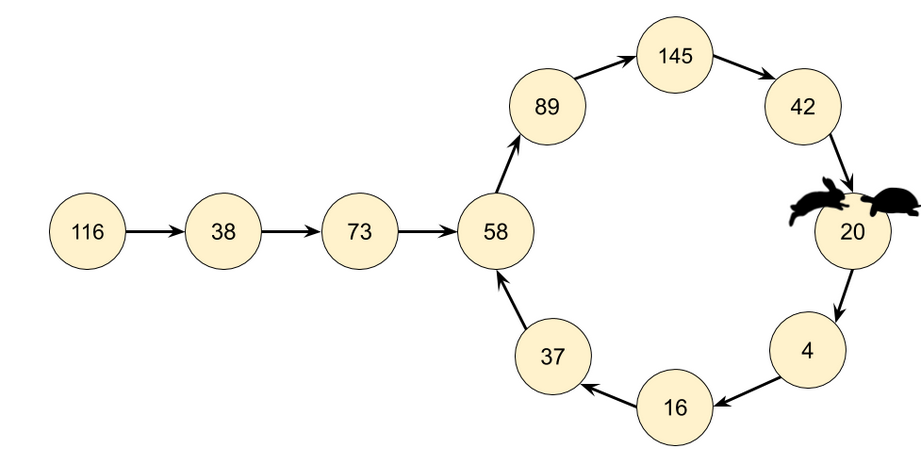
此时可以定义两个指针，一个快指针，一个慢指针。快指针一次能走两格，慢指针只能一次走一格 。但是两者最后都会遇到，如果快指针先遇到1则结束循环或者龟兔两者相遇，此时就需要判断两者的数字，如果遇到的值并不是1，那么就说明不存在快乐数。

4.代码

LeetCode代码

class Solution {public boolean isHappy(int n) {int slowPointer = n;int quickerPointer = getNext(n);while (quickerPointer!=1 &&quickerPointer!=slowPointer){quickerPointer = getNext(getNext(quickerPointer));slowPointer = getNext(slowPointer);}return quickerPointer==1;}public int getNext(int n){int sum =0;while (n>0){sum += Math.pow(n%10,2);n = n/10;}return  sum;}
}

时间复杂度O(logn)空间复杂度O(1)

具体案例代码：

package LeetCode19;public class javaDemo {public static void main(String[] args) {boolean flag ;int n = 4;
//        乌龟int slowPointer = n;
//        兔子int quickerPointer = getNext(n);
//        当兔子不是1或者两者还未相遇的时候则两者继续前进while (quickerPointer!=1 &&quickerPointer!=slowPointer){quickerPointer = getNext(getNext(quickerPointer));slowPointer = getNext(slowPointer);}
//        当兔子遇到1或者龟兔相遇时候判断龟兔相遇的时候值是否为1flag = quickerPointer==1;
//        输出结果System.out.println(flag);}
//    计算每一个的数字的平方和public static  int getNext(int n){
//        定义累计和int sum =0;while (n>0){sum += Math.pow(n%10,2);n = n/10;}return  sum;}
}

---