Https

• Http协议

Http协议是目前应用比较多应用层协议，浏览器对于Http协议已经实现。Http协议基本的构成部分有

1. 请求行 ： 请求报文的第一行
2. 请求头 ： 从第二行开始为请求头内容的开始部分。每一个请求头都是由K-V键值对组成。
3. 请求体： 请求头完成后以空行结束、从空行开始为请求体。

---

同理，Http响应也遵循上述基本结构

1. 响应行：响应报文的第一行，主要包含了Http的版本、响应状态码。
2. 响应头：从第二行开始为响应头内容的开始部分，每一个响应头都是由K-V键值对组成。
3. 响应体：服务器器所有的响应内容都在响应体中返回，当然有些请求可能也没有响应体，例如302重定向请求。

所谓的协议就是 ： 为了满足计算机通信双方可以正确的获取数据，处理数据而约定好的一种格式，如果不遵守协议，则无法正确处理数据。例如Http协议的响应行没有状态码，或者响应头格式不正确等都会导致浏览器无法正确解析。
遵循了标准Http协议，浏览器和服务器则可以根据对方传输的信息做正确处理，浏览器也可以正确展示数据。

---

之前的版本Http协议都是在浏览器与服务器之间使用明文传输的，这种方式是不安全的，极度容易被中间人攻击篡改传输的数据。于是Https协议诞生了。

• Https起源

1. 对称加密算法实现

既然Http协议是不安全的，那将传输的信息使用对称加密算法加密过后再传输就可以避免被中间人攻击了，但问题是，如何让对称加密的密钥让浏览器与服务器更安全的知道？如果浏览器直接将密钥发给服务器，那还是有可能被攻击者解惑，则后续再传输的任何信息都可以被轻松解密，所以对称加密也是不安全的。

2. 非对称加密算法实现

非对称加密算法有以下优势：

1. 有两把密钥，分为公钥和私钥，公钥加密只能私钥解密，而私钥加密只能公钥解密。
2. 密钥长度更长，破解难度更高。
3. 攻击者获取一把密钥无法实现对数据的加解密。

尝试用非对称加密算法来实现浏览器与服务器的安全通信

---

1. 首先服务器把自己的公钥发送给浏览器
2. 浏览器用服务器的公钥加密一串随机数字
3. 将加密后的密文发送给服务器，即使被中间人攻击，由于私钥只有服务器才有，也是无法解密的。
4. 服务器拿到密文，用自己的私钥进行解密，这样就可以获取到浏览器生成的随机数，后续用这个随机数进行对称加密即可。

常用的非对称加密实现算法有 RSA、DSA、SM2等。
绝大多数的非对称加密算法都是基于数学问题去实现的，例如RSA算法基于超大质数分解，SM2基于椭圆曲线率等。 在可预见的时间范围内，这几种算法的安全性依然是相当高的。

SSL、TSL

• 非对称加密潜在的问题

在使用了非对称加密算法保证浏览器与服务器通信安全以后，似乎还是有一个问题没有解决，那就是如果服务器发送给浏览器公钥的过程中被中间人拦截，中间人替换成自己的公钥发送给浏览器，那么浏览器再用假的公钥加密随机数，发给服务器，此时再度被中间人攻击，由于浏览器加密用的是假的公钥，所以攻击者可以用自己的私钥进行解密，然后再用浏览器的公钥加密，发给浏览器，这个时候，攻击者已经完全拿到的浏览器生成的随机数了，那么后续双方的通信也都可以被轻松破解。

• 问题解决

可以看到，根本的问题就是浏览器无法判断服务器发过来的公钥是不是服务器本身的还是被篡改的，此时就需要引入一个第三方机构了，这个第三方机构就是CA （Certificate Authority）。

---

服务器会像自己的域名信息、组织、主体以及最关键的公钥整理好，向CA机构申请颁发证书，CA机构经过审核以后，用自己的私钥对这些信息进行数字签名，也就是先将信息进行消息摘要，然后对这个消息摘要进行加密，然后将CA的公钥以及申请的信息打包成一个证书
CA会将证书下发给服务器。那么后续的通信过程是这样的：

---

1. 浏览器向服务器发送请求，服务器会将自己的证书发给浏览器。
2. 浏览器首先根据证书上的CA机构的公钥对密文进行解密，然后拿着解密的内容去比对证书上的数字签名是否一致，如果不一致，则表示证书有问题。如果攻击者篡改了篡改了服务器的公钥，则浏览器再进行数字签名验证时，就会出现问题，此时会提示风险。
3. 如果攻击者也申请了一个证书来伪造，虽然可以正确解密出来，但两个域名的证书内容是不可能相同的，所以也无法验证成功，例如 访问的是 www.bilibili.com，而证书上的域名是 www.bi1ibi1i.com，此时也会提示证书安全问题。

---

此时看似解决了安全问题，但现在的问题是，浏览器如何知道CA机构的公钥不是被篡改过的呢？这就有点套娃了。
最简单的办法就是操作系统和浏览器直接内置了CA机构的公钥信息，内置的方式避免了攻击者篡改。

可以发现，上述将的浏览器和服务器的协商密钥的过程是独立于Http协议之外的，这一过成叫做
secure socket layer (安全套接字层)，也就是 SSL，SSL经历过多次迭代发展后有了SSL1.0、SSL2.0、SSL3.0，后来更名为TSL。
所以SSL、TSL是独立于协议之外的一套安全机制，这一过程也称作SSL握手。

除此之外，证书也设置有效期、定义更换算法以及密钥也是提升安全性的一种方式。

• CA机构

Symantec：赛门铁克（Symantec）SSL证书前身为 Verisign，后于2017年12月被DigiCert收购，现在已经使用 DigiCert 根证书。Symantec Secure Site SSL证书依然是各行业尤其是金融银行证券等大型企业认可的品牌。Symantec Secure Site SSL证书 支持诺顿安全签章，是网站拥有很好的可信度。
GeoTrust：是全球成长最快的数字证书颁发机构之一，在全球超过150个国家/地区颁发数百万的数字证书。
Comodo：是全球知名的互联网安全公司，为用户提供网站安全防护、SSL证书、反病毒软件等服务。
DigiCert：是全球领先的数字证书提供商，在SSL市场占有重要地位。DigiCert旗下拥有DigiCert、Symantec、Geotrust、Thawte、Rapid 5大SSL证书品牌，可以提供从基础型到高端型全系列的SSL证书解决方案。

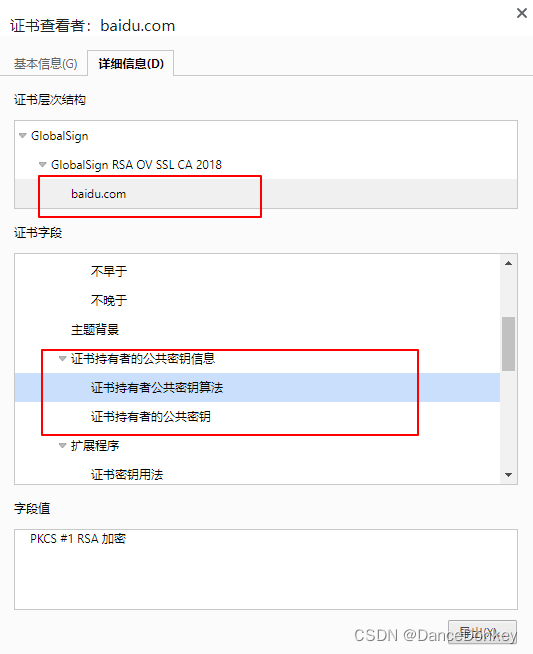
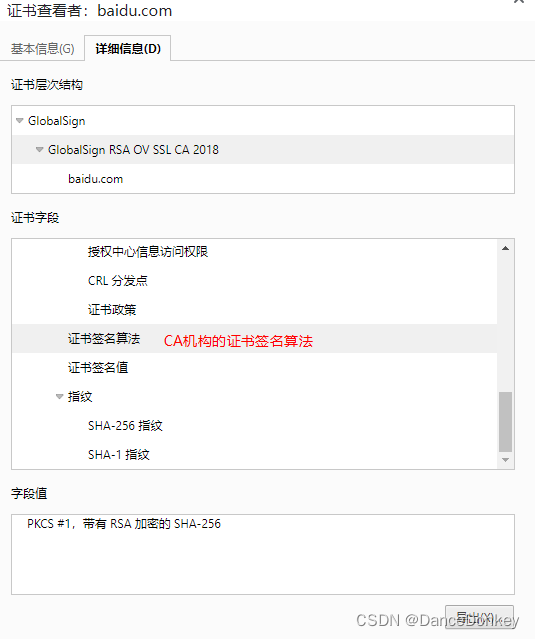
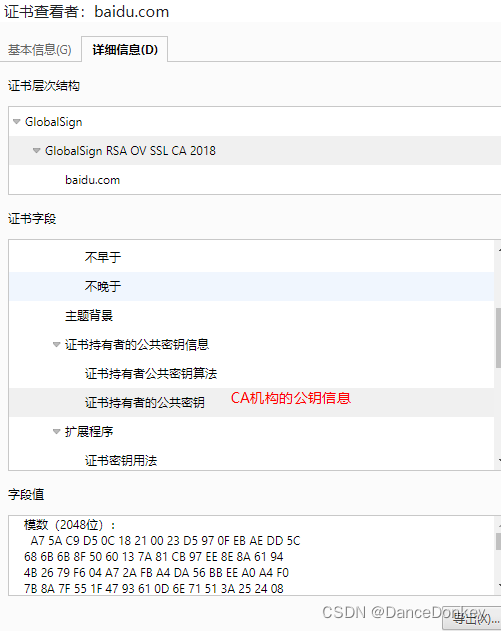
证书的基本信息有颁发者、颁发机构等等

同时，证书中还包含了服务器的公钥、域名、CA机构的公钥、签名算法等等。