前段时间有粉丝私信想让我出一期对时间序列预测的文章,所以今天它来了。

时间序列数据,如股指价格,具有波动性、非线性和突变的特点,对于这类数据的预测往往需要可靠强健的预测模型,而传统的机器学习算法如SVM、BP等,大都采用误差最小化或反向传播来改进预测性能,大量参数调整、复杂的模型架构以及迭代时间长让这些模型逐渐落后。
而极限学习机ELM和核极限学习机KELM能够很好的克服这些问题,作者在前面的文章中介绍了ELM和KELM的原理及其实现,ELM具有训练速度快、复杂度低、克服了传统梯度算法的局部极小、过拟合和学习率的选择不合适等优点,而KELM则利用了核学习的方法,用核映射代替随机映射,能够有效改善隐层神经元随机赋值带来的泛化性和稳定性下降的问题,应用于非线性问题的性能更优[1]。
因此作者将用KELM和ELM结合作者前面提到的优化算法来预测股指的变化,并将之与BP神经网络这类传统机器学习算法进行对比。
00目录
1 PSO-KELM模型
2代码目录
3 预测性能
4 展望
参考文献
01 PSO-KELM模型
1.1 PSO与KELM原理
PSO即粒子群优化算法,KELM即核极限学习机,作者在前面的文章中讲解过其具体原理,文章链接如下,这里不再赘述。
KELM核极限学习机原理及其实现
1.2 样本选取与预处理
以某股的开盘价作为研究样本,有效数据共554个,考虑用前20日的开盘价预测第21日的开盘价,即以20个数据作为一个样本进行滚动预测,一共可得到534个样本,选取前70%的样本作为训练数据,后30%作为测试数据。
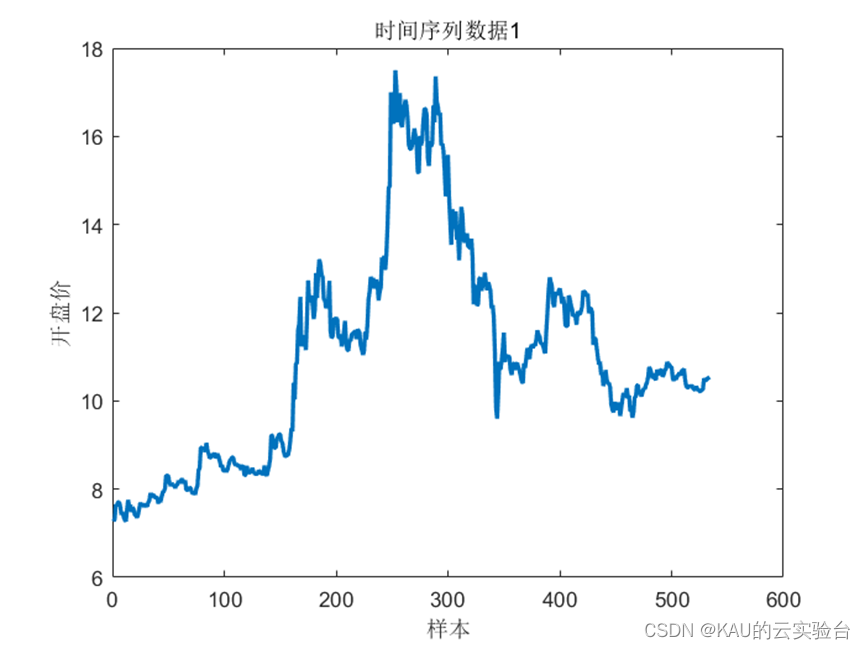
原始数据间差波动范围比较大,会影响模型稳定性和预测精度。因此在把开盘价数据输入之前,首先需要对数据进行预处理即归一化本文对原始数据进行归一化处理,将样本数据处理到区间[0, 1]之间,归一化公式为
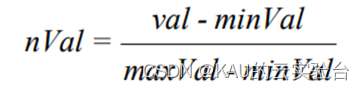
minVal为数据序列中的最小值,maxval为数据序列最大值。
1.3 PSO-KELM预测模型
将PSO与KELM结合,以KELM模型预测的MAE作为PSO的适应度,该模型流程如下:

02 代码目录

其中,MY_XX_Reg.m都是可单独运行的主程序,而result.m用于对比不同算法预测效果,result.m可依次运行4个MY_XX_Reg.m,并对其预测结果进行对比。
03 预测性能
3.1 评价指标
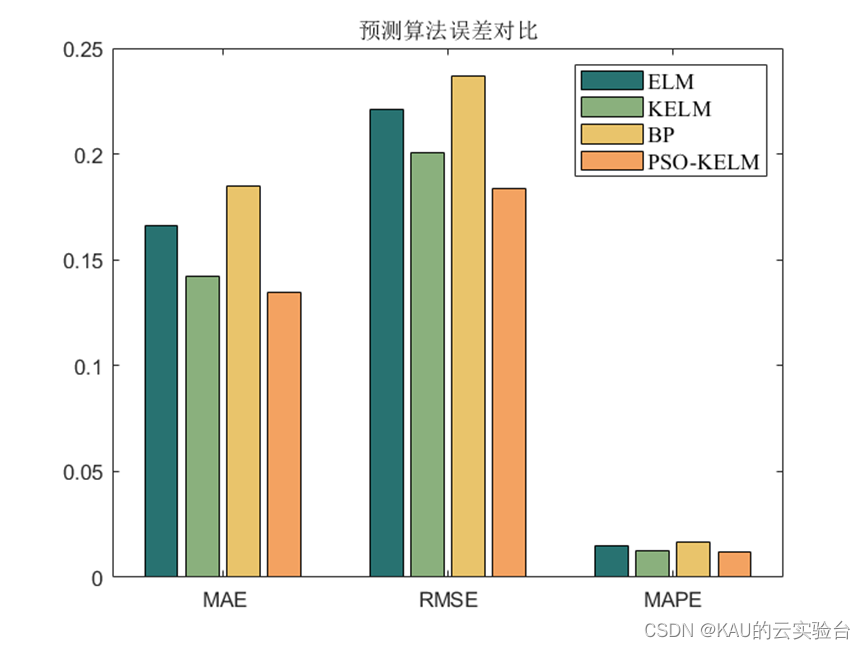
为了验证预测结果的准确性和精度,分别采用均方根差(Root Mean Square Error,RMSE) 、平均绝对百分误差( Mean Absolute Percentage Error,MAPE) 和平均绝对值误差 ( Mean Absolute Error,MAE) 作为评价标准。
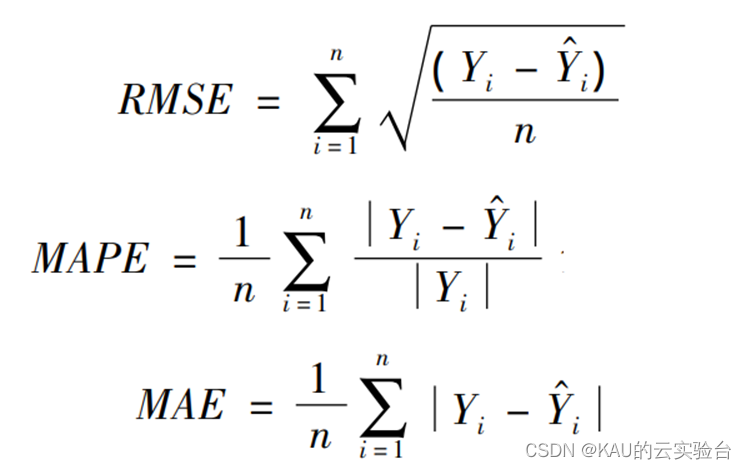
式中 Yi 和Y ^ i分别为真实值和预测值; n 为样本数。
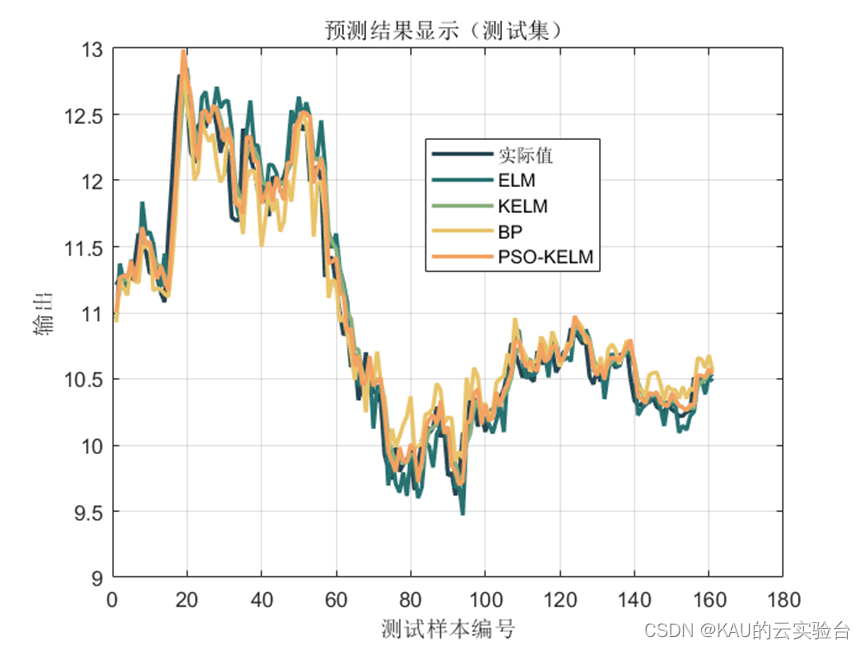
3.2 结果对比
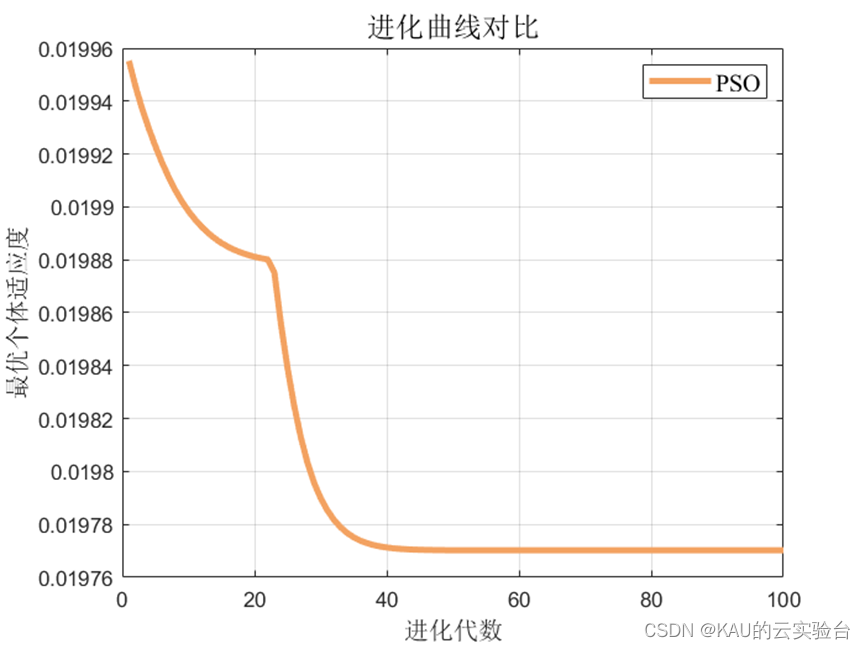
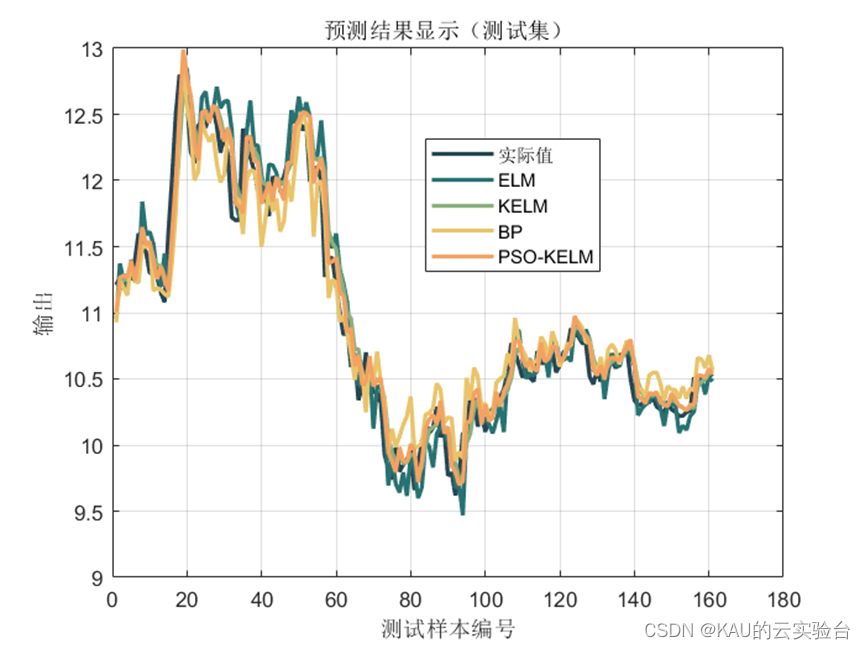

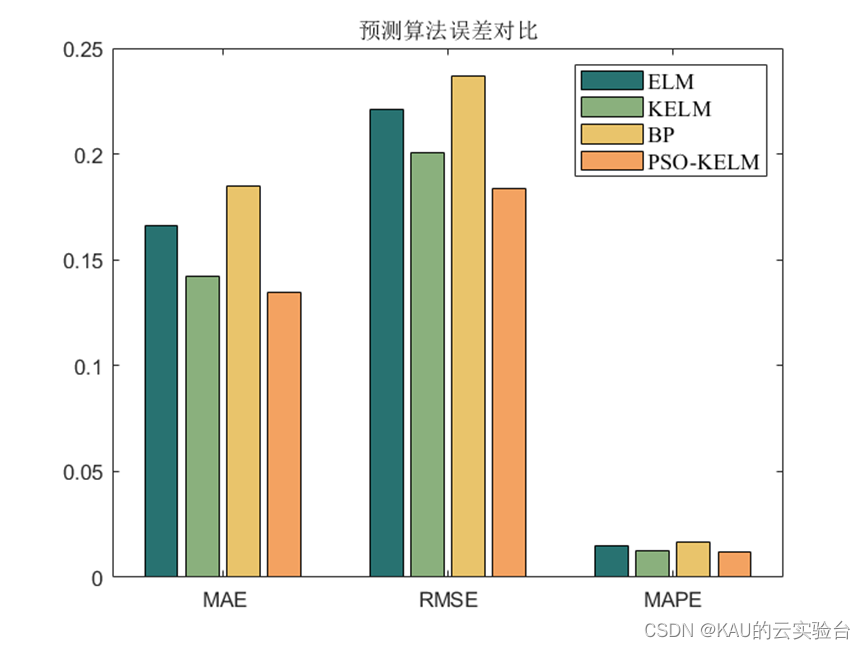
可以看出,预测模型中,经PSO优化后的KELM预测模型取得了不错的效果,同时,也可以引入作者前面提到的各种改进算法提高PSO的寻优性能,以取得更佳的效果
04 展望
在这一篇文章中作者实现了PSO-KELM对于时间序列数据的预测,并对比了ELM和BP。后面作者将介绍蜣螂优化算法及其改进,这也是一位粉丝朋友私信我的,KAU本着有求必应的原则(能力范围内~)给安排了
以上
源码获取
可私信作者
参考文献
[1] Huang G B,Zhou H M,Ding X J,et al.Extreme learning machine for regression and multiclass classification[J].IEEE Transactions on Systems, Man,and Cybernetics,Part B (Cybernetics),2012,42(2):513.
另:如果有伙伴有待解决的优化问题(各种领域都可),可以发我,我会选择性的更新利用优化算法解决这些问题的文章。
如果这篇文章对你有帮助或启发,可以点击右下角的赞/在看(ง •̀_•́)ง(不点也行),若有定制需求,可私信作者。