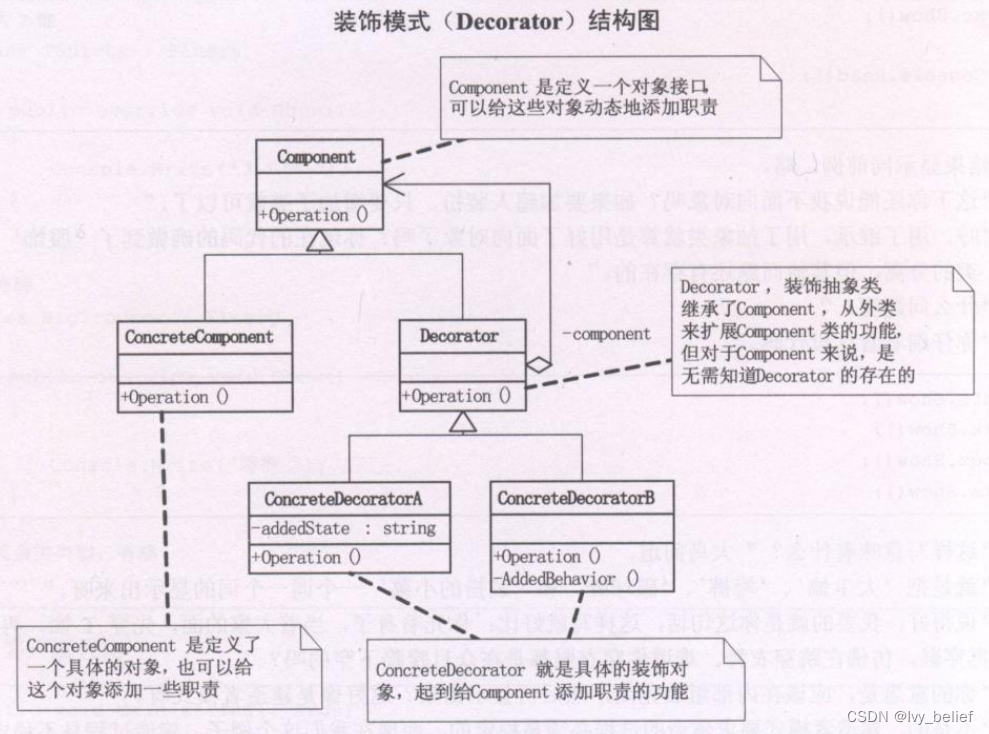
LCS最大公共子序列与 LIS最大递增子序列

LCS

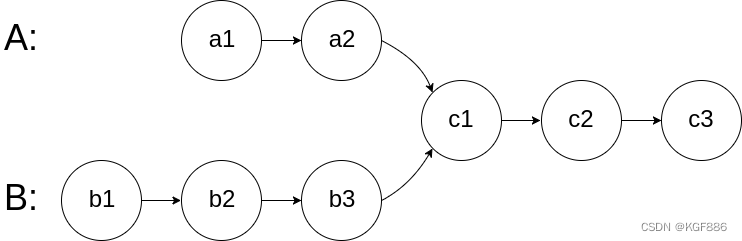
Largest Common Subsequence 最大公共子序列

/*
Input
s1 s2//两个字符串Output
length//长度
ans//具体字母
*/
#include<iostream>
using namespace std;
int main()
{string s1,s2;cin>>s1>>s2;int dp[100][100]={0};//dp[i][j]表示s1取前i位，s2取前j位时的最大公共长度int n=s1.size(),m=s2.size();s1=" "+s1;s2=" "+s2;//使范围从[0,n-1]变为[1,n]for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(s1[i]==s2[j]){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}}cout<<dp[n][m]<<endl;//最大公共长度 完成//以下为输出具体方案 公共部分string ans;while(n>=1&&m>=1){if(s1[n]==s2[m]) ans=s1[n]+ans,n--,m--;//条件为两个字母相等，同时n,m也需要更新else if(dp[n][m-1]>dp[n-1][m]) m--;else n--;}cout<<ans<<endl;
}

dp数组的变化如图：
在这里插入图片描述

LIS

Largest Increasing Sunsequence 最大递增子序列

/*
Input
n
a1 a2 a3...an//n个数Output 
ans //长度
*/#include<iostream>
using namespace std;
int main()
{int n;cin>>n;int a[n+2];int dp[n+2]={0};//dp[i]表示前i个数最大上升序列长度for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=n;i++){dp[i]=1;for (int j = 1; j <= i; j++)//搜索1~i范围{if (a[i] > a[j])dp[i] = max(dp[i], dp[j] + 1);}}int ans=0;for(int i=1;i<=n;i++)ans=max(ans,dp[i]);cout<<ans<<endl;
}