On Measuring and Controlling the Spectral Bias of the Deep Image Prior
文章目录
- On Measuring and Controlling the Spectral Bias of the Deep Image Prior
- 1. 方法原理
- 1.1 动机
- 1.2 相关概念
- 1.3 方法原理
- 频带一致度量与网络退化
- 谱偏移和网络结构的关系
- Lipschitz-controlled 卷积层
- Gaussian-controlled 上采样层
- 自动停止迭代过程
- 2. 实验结果
- 3. 总结
文章地址:https://arxiv.org/pdf/2107.01125.pdf
代码地址: https://github.com/shizenglin/Measure-and-Control-Spectral-Bias
参考博客: https://zhuanlan.zhihu.com/p/598650125
1. 方法原理
1.1 动机
动机
- Deep Image Prior已经被广泛地应用于去噪、超分、图像恢复等
- 但是我们尚不清楚如何在网络架构的选择之外控制DIP
- DIP存在性能达到峰值之后退化的问题 --> 需要early stopping
贡献
- 使用谱偏移度量和解释 DIP的原理
- DIP学习目标图像低频分量的效率比高频分量高
- 控制谱偏移
- 使用Lipschitz-controlled 正则化和 Lipschitz 批归一化加速和稳定优化过程
- 使用 上采样方法(bilinear upsampling)引入了倾向于恢复低频分量的特点(谱偏移)
- 使用了一种简单的early stopping策略防止多余的计算
1.2 相关概念
谱偏移原则是指:神经网络拟合低频信息的效率比高频信息快
相关文章参考:
- On the Spectral Bias of Neural Networks
- FREQUENCY PRINCIPLE: FOURIER ANALYSIS SHEDS LIGHT ON DEEP NEURAL NETWORKS
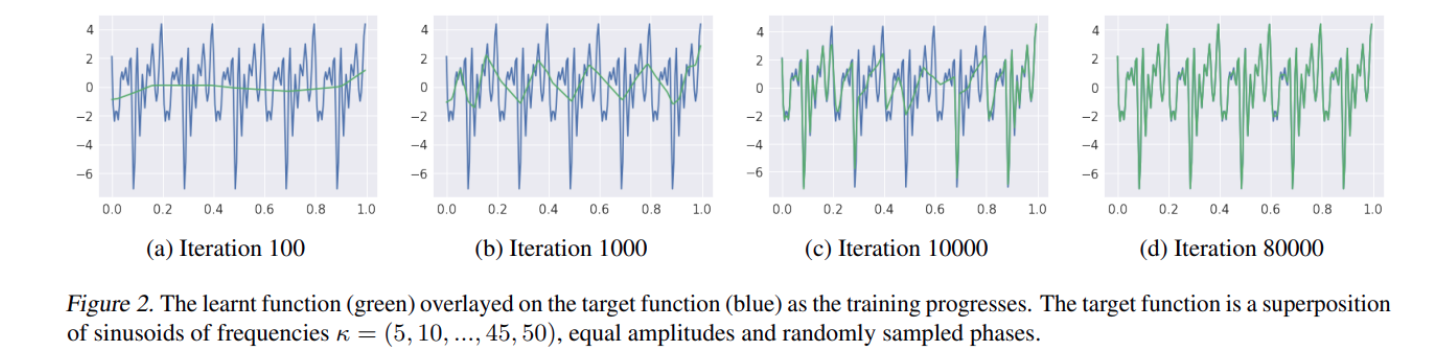
用其中的一些图进行解释:
- 随着迭代的进行,神经网络的输出(绿色线)首先拟合的是真实观测数据的低频,然后再去逐渐拟合高频
反(逆)问题:根据观测结果获取真实模型的一种求解模式。具体的可以参考
- Untrained Neural Network Priors for Inverse Imaging Problems: A Survey
注意反问题求解存在一个普遍的问题:多解性。也就是多个反演结果的合成数据都可以和观测数据匹配。通常一个减少多解性的方法就是添加约束条件(在公式中表现为正则化约束)
1.3 方法原理
频带一致度量与网络退化
这篇文章是从频率域的角度进行谱偏移分析的,用 { θ 1 , . . . , θ T } \{\theta^{1},...,\theta^{T}\} {θ1,...,θT}表示第对应迭代次数网络的参数,用 { f θ 1 , . . . , f θ T } \{f_{\theta^{1}},...,f_{\theta^{T}}\} {fθ1,...,fθT}表示对应的网格过程。对图片频率分析需要使用傅里叶变换获得 频率域的信息,用 F ( f θ ( t ) ) F(f_{\theta^{(t)}}) F(fθ(t))表示。频谱图的表示如下:

如果对标签图片也做一次傅里叶变换,那么可以求解网络输出和这个结果的比值
H θ ( t ) = F { f θ ( t ) } F { y 0 } H_{\theta^{(t)}} = \frac{F\{f_{\theta^{(t)}}\}}{F\{y_0\}} Hθ(t)=F{y0}F{fθ(t)}
- 这个比值越接近于1表示网络输出和标签的相关性越高
- H图像是一个以中心对称的图像,这里为方便统计就将其分割成为多个同心圆环,求圆环中的平均值作为这个圈内的值。也就是将一个二维的度量变为了一个一维的度量。
- 文章中将频率划分为了:lowest、low、medium、high和highest五个部分

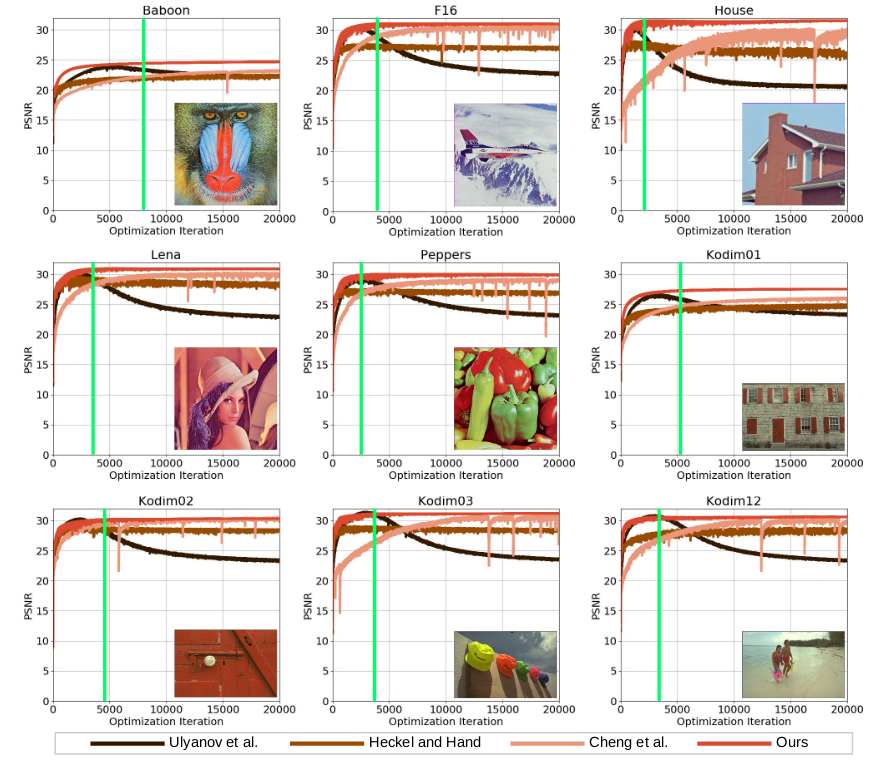
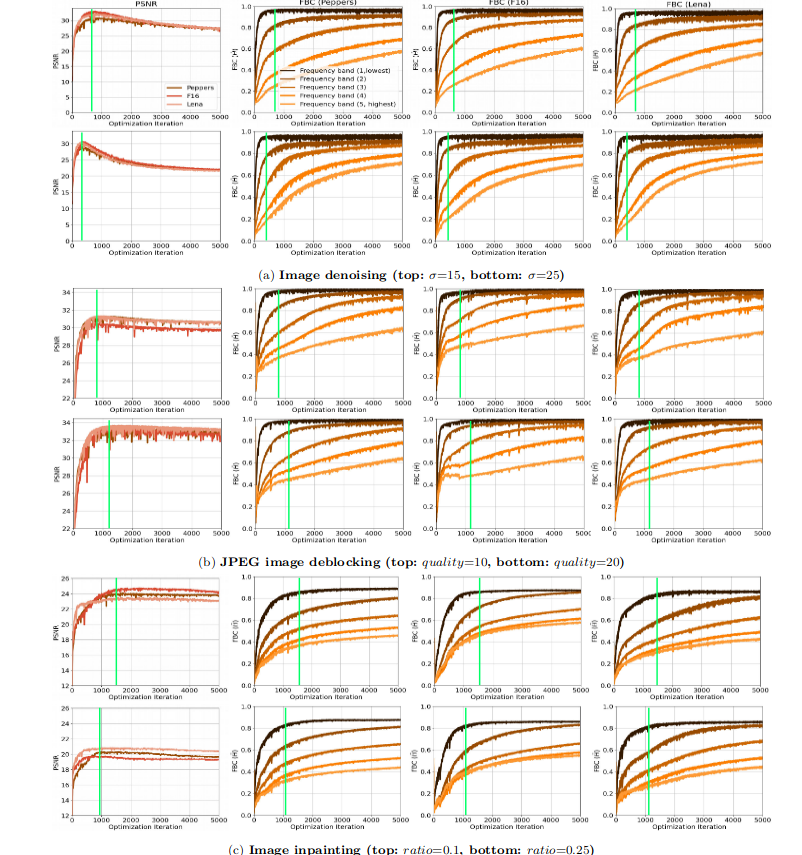
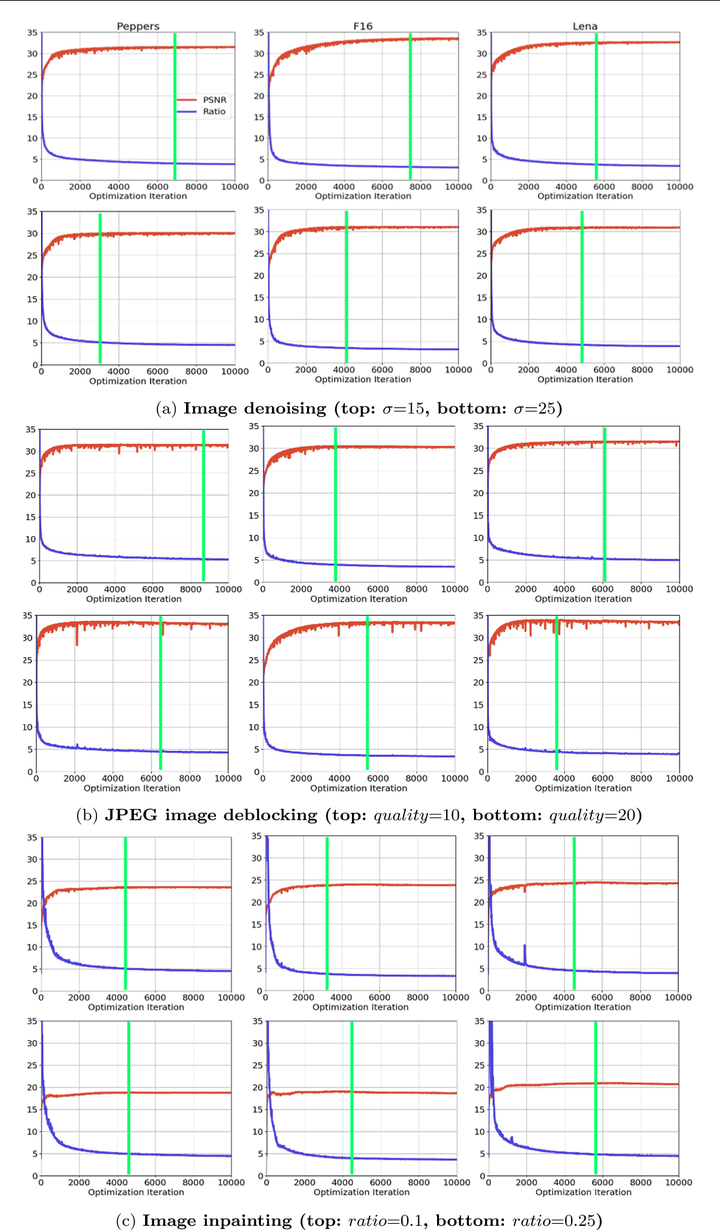
这个度量比值在DIP不同应用场景中随着迭代次数的变化
- 随着DIP迭代次数的增加,PSNR会先达到最高然后缓慢降低(性能达到峰值之后会下降)
- 在PSRN最高的时候(图中绿线),恰好是lowest分量的频带一致性刚好最高的时候
- 通过下图验证了 DIP也存在谱偏移的现象:低频分量学得更快且频带一致性很高,而高频分量学习相对较慢且频带一致性较低
- 随着高频部分的频带一致性提高,PSNR下降
谱偏移和网络结构的关系
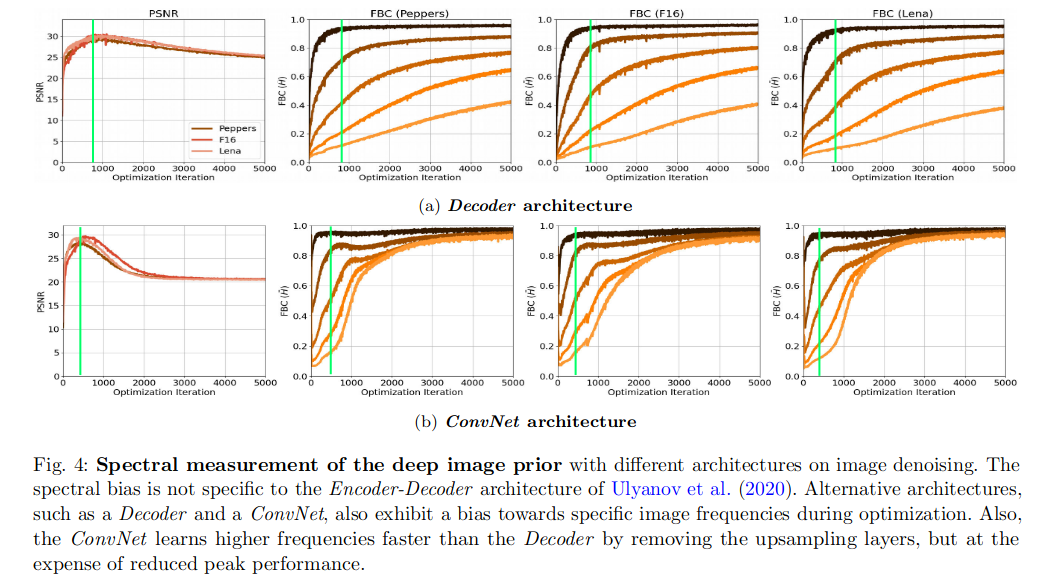
前面有研究表示Encoder-Decoder结构的DIP效果更好,这里作者对比了三种不同结构进行测试对比(a. 没有Encoder部分的DIP; b. 没有上采样层的DIP;):
- 不论什么结构谱偏移都存在
- 去掉上采样层的Decoder结构(ConvNet)拟合高频的效率更高,这里表现为高频部分的频带一致性高
- 无上采样层的ConvNet结构最大的PSNR比Decoder和DIP低
结论
- 无训练网络UNNP可以解决逆图像问题的原因是:低频学习效率高,高频学习效率相对较慢(谱偏移)
- 高频信息通常为为结构高频信息和噪声高频信息,当网络开始学习噪声高频信息的时候,网络恢复的性能开始下降
- 这里通过一个类似消融实验的方法说明上采样层是可以提高PSNR的,但是这会影响低频的收敛速度
防止网络退化,平衡性能与效率的方向
- 保证性能的前提下,使用参数量更少的 Decoder结构 替代DIP的 Encoder-Decoder结构
- 性能退化:抑制网络对高频噪声的学习(使用上采样层)
- 加速收敛:使用更合适的上采样层
- 提前停止策略:自动检测?
Lipschitz-controlled 卷积层
从频率域理解卷积操作
- 对一个时间域/空间域的变量做一个傅里叶变换其实是将作用域变换到了频率域,这样的其中一个作用是:
- 将空间域的卷积操作 变为 频率域的乘积操作,简化计算
- 当然对于信号处理还有更多的好处,比如FK变换可以用于滤波
- 图像和“卷积核”的作用在频率域其实就是一个乘积过程
卷积核具有滤波的作用,但是什么样的卷积核可以抑制高频呢?
L-Lipschitz连续
这个概念很有意思,WGAN-GP中也用到了
其定义是:如果函数f在区间Q中,以常数L Lipschitz连续,那么对于 x , y ∈ Q x,y \in Q x,y∈Q有:
∣ ∣ f ( x ) − f ( y ) ∣ ∣ ≤ L ∣ ∣ x − y ∣ ∣ ||f(x)- f(y)|| \leq L||x - y|| ∣∣f(x)−f(y)∣∣≤L∣∣x−y∣∣
常数L就被称为函数f在区间Q上的 Lipschitz常数。Lipschitz连续其实是限制了连续函数f的局部变动幅度不能超过某一个常量。我个人感觉一个非常更简单地理解这个概念的方法就是将稍微变动一下这个公式:
∣ ∣ f ( x ) − f ( y ) ∣ ∣ ∣ ∣ x − y ∣ ∣ ≤ L \frac{||f(x)- f(y)||}{||x - y||} \leq L ∣∣x−y∣∣∣∣f(x)−f(y)∣∣≤L
这个东西看起来就像是求导了,更多的可以参考https://blog.csdn.net/FrankieHello/article/details/105739610

结合Lipschitz和频谱分析
假设卷积层的 f f f是符合C-Lipschitz的,存在:
∣ f ^ ( k ) ∣ ≤ C ∣ k ∣ 2 ≤ ∣ ∣ w ∣ ∣ s n ∣ k ∣ 2 |\hat{f}(k)| \leq \frac{C}{|k|^2} \leq \frac{||w||_{sn}}{|k|^2} ∣f^(k)∣≤∣k∣2C≤∣k∣2∣∣w∣∣sn
- k表示频率, ∣ f ^ ( k ) ∣ |\hat{f}(k)| ∣f^(k)∣表示傅里叶系数的模(有实部和虚部)
- 分母是 k 2 k^2 k2表示在高频的时候衰减很强,学习更高的频率需要更高的频谱范数(分子)
- ∣ ∣ w ∣ ∣ s n ||w||_{sn} ∣∣w∣∣sn 表示卷积层参数矩阵w的谱范数,可以通过限制谱范数的上限来限制卷积层学习更高频率的能力
- ∣ ∣ w ∣ ∣ w ∣ ∣ s n ∣ ∣ s n = 1 ||\frac{w}{||w||_{sn}}||_{sn} = 1 ∣∣∣∣w∣∣snw∣∣sn=1, ∣ ∣ w λ ∣ ∣ w ∣ ∣ s n ∣ ∣ s n = λ ||\frac{w\lambda}{||w||_{sn}}||_{sn} = \lambda ∣∣∣∣w∣∣snwλ∣∣sn=λ
- w m a x ( 1 , ∣ ∣ w ∣ ∣ s n / λ ) \frac{w}{max(1,||w||_{sn}/\lambda)} max(1,∣∣w∣∣sn/λ)w
注意这里我们想要达到的一个效果就是:限制最高可以学习的频率。可以选择一个合适的 λ \lambda λ在保证恢复效果的同时不去恢复噪声信号。
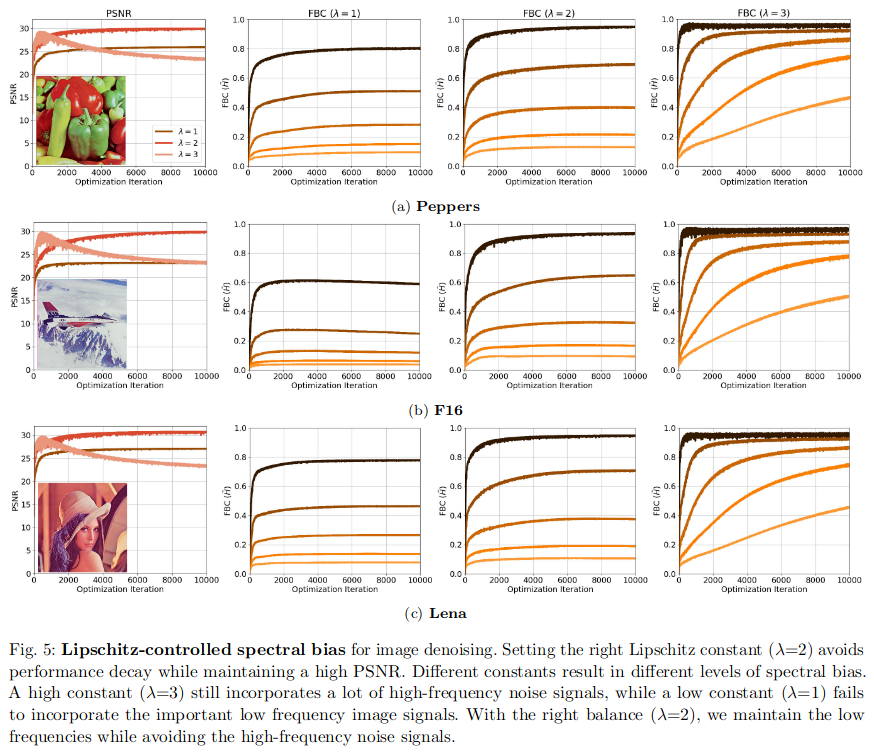
其他网络层对Lipschitz常数的影响

Gaussian-controlled 上采样层
插值、邻近上采样层的平滑操作会让DIP网络收敛速度变慢,但是上采样层对于抑制高频信息又有一定的作用,为了平衡二者作者引入了 gaussian-controlled上采样层。
方法就是:转置卷积 + 高斯核
- 转置卷积可以自定义上采样的卷积核

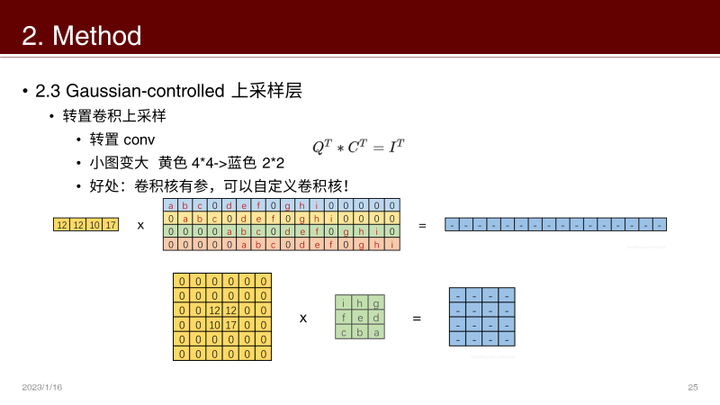
- 为了控制平滑程度,卷积核最简单的就是高斯核

- 实验不同的高斯核: σ \sigma σ越小收敛越快,但是PSNR越小

自动停止迭代过程
- 利用Lipschitz方法限制了网络学习的最高频率噪声,避免了网络的退化
- 当高频部分到达了上界限,也就意味着网络在之前就已经收敛了
- 怎么评估高频到达了上界限
- r = B l u r r i n e s s S h a r p n e s s r = \frac{Blurriness}{Sharpness} r=SharpnessBlurriness
- 即当模糊度/锐度之间的导数小于预先设置的阈值的时候,停止迭代
- r ( f θ ) = B ( f θ ) / S ( f θ ) r(f_{\theta}) = B(f_{\theta})/S(f_{\theta}) r(fθ)=B(fθ)/S(fθ)
- Δ r ( f θ ( t ) ) = ∣ 1 n ∑ i = 1 n r ( f θ ( t − n − i ) ) − 1 n ∑ i = 1 n r ( f θ ( t − n − i ) ) ∣ \Delta r(f_{\theta ^{(t)}}) = |\frac{1}{n}\sum_{i=1}^{n}r(f_{\theta}^{(t-n-i)}) - \frac{1}{n}\sum_{i=1}^{n}r(f_{\theta}^{(t-n-i)})| Δr(fθ(t))=∣n1i=1∑nr(fθ(t−n−i))−n1i=1∑nr(fθ(t−n−i))∣
2. 实验结果
-
去噪
-
-
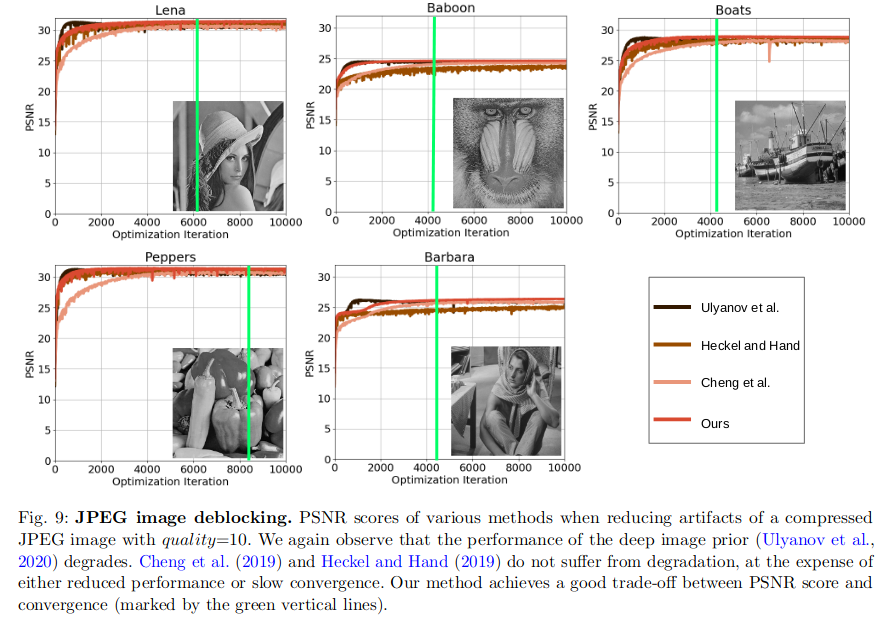
Image deblockign
-
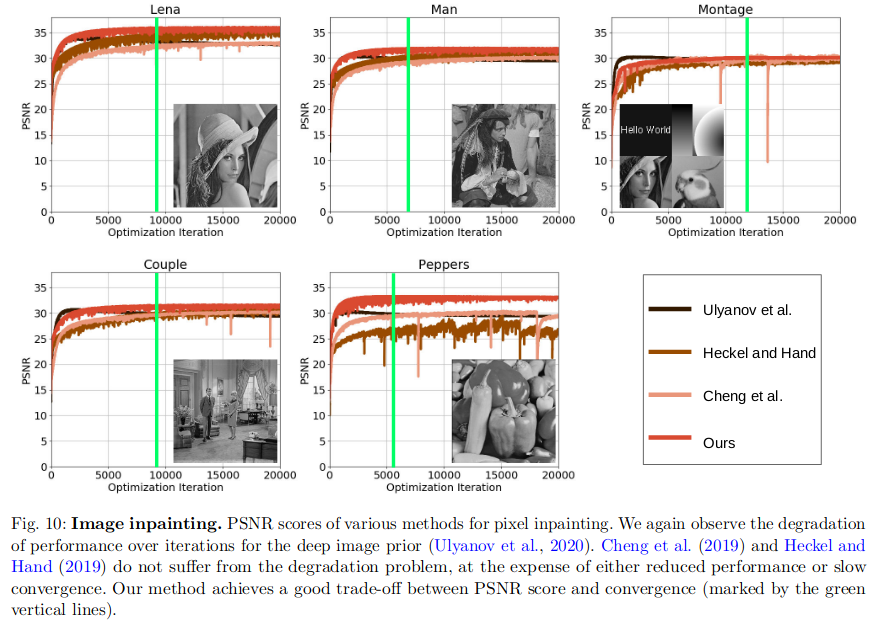
Image Inpainting
-
3. 总结
研究思路
- 从谱偏置方向分析DIP的工作,网络先拟合低频信息,逐渐拟合高频信息
- 怎么控制拟合高频信息?–> 高频截断 --> 应用Lipschitz理论控制,解决网络层退化的问题
- 网络训练慢怎么解决?–>分析发现常规的上采样层相当于一个低通滤波器,引入了过多的低频分量导致很多时候收敛非常慢,所以使用 gaussian 核控制的转置卷积方法 平衡网络收敛效率的问题。
- 怎么Early stopping 减少迭代次数? --> 使用模糊度与锐度的比值的导数进行衡量
优点
- 将GAN 谱优化的策略放到DIP之中,在频率域中分析各个层的性质:低频收敛快,高频收敛慢。
- 用谱偏置的思路解释了网络退化问题
- 提出频带一致性、模糊度和锐度比值梯度 平衡了DIP收敛效率和效果
改进方向
- 就个人观点:噪声这里假设都是高频的,但是低频噪声、结构噪声是否会有影响?
- 该研究给实际应用DIP提供了很大的可能性,但是就实验效果来看并没有提升,甚至有所下降。所以基于这种方法怎么去同时提高效果?
- 就我个人想法:继续减少参数化网络的参数量(PIP等工作),并且提高恢复的效果(持续研究方向) 是现在的研究方向。