opencv进阶01-直方图的应用及示例cv2.calcHist()

直方图是什么？

直方图是一种图形表示方法，用于显示数据中各个数值或数值范围的分布情况。它将数据划分为一系列的区间（也称为“箱子”或“bin”），然后统计每个区间中数据出现的频次（或频率）。直方图可以帮助我们更好地理解数据的分布特征，包括集中趋势、离散程度等。

直方图的主要特点包括：

1. 横轴（X 轴）： 横轴表示数据的数值范围或区间。每个区间通常由两个数值来表示，例如，0-10、10-20 等。

2. 纵轴（Y 轴）： 纵轴表示每个区间中数据的频次（或频率），也就是该区间内数据出现的次数。

3. 条形图： 直方图的图形由一系列的矩形条组成，每个矩形条的宽度表示区间的宽度，高度表示该区间内数据的频次。

4. 连续数据： 直方图适用于连续型数据，例如测量数据、时间数据等。对于离散型数据，柱状图可能更为适合。

直方图在许多领域有重要的应用，包括统计学、图像处理、数据分析等。在图像处理中，直方图可以用来分析图像的像素值分布，从而进行图像增强、对比度调整、图像分割等操作。在统计学中，直方图可以帮助我们了解数据的分布情况，如正态分布、偏态分布等。通过观察直方图，我们可以对数据的特征有更深入的了解，从而做出更准确的决策和分析

直方图在图像中的含义

从统计的角度讲，直方图是图像内灰度值的统计特性与图像灰度值之间的函数，直方图统计图像内各个灰度级出现的次数。从直方图的图形上观察，横坐标是图像中各像素点的灰度级，纵坐标是具有该灰度级（像素值）的像素个数。

例如，有一幅图像如图 13-1 所示。该图中只有 9 个像素点，存在 1、2、3、4、5，共 5 个灰度级。

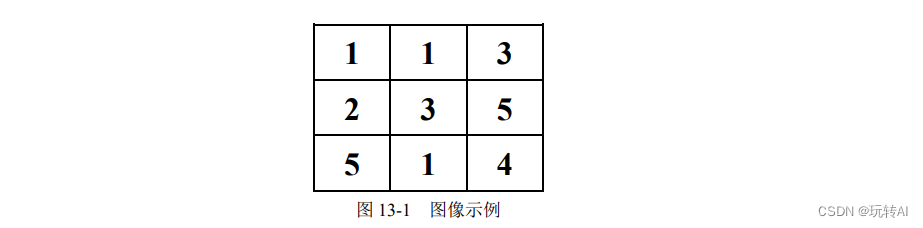
在这里插入图片描述

统计各个灰度级出现的次数，如表 13-1 所示

在这里插入图片描述
在绘制直方图时，将灰度级作为 x 轴处理，该灰度级出现的次数作为 y 轴处理，则可知：

  • x 轴的数据为 x=[1 2 3 4 5]。
  • y 轴的数据为 y=[3 1 2 1 2]。

根据上述关系，可以绘制出如图 13-2 所示的折线图（左图）和直方图（右图）。一般情况下，我们把左侧的直线图和右侧直方图都称为直方图。

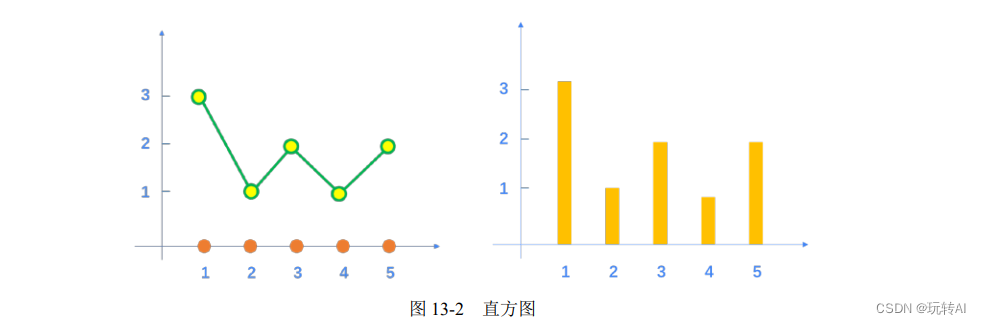
在这里插入图片描述

在实际处理中，图像直方图的 x 轴区间一般是[0, 255]，对应的是 8 位位图的 256 个灰度级；y 轴对应的是具有相应灰度级的像素点的个数。

例如在图 13-3 中，上图是一张图像，下图则是其对应的直方图。图中圆点表示这些像素点会被统计到对应的灰度级上。

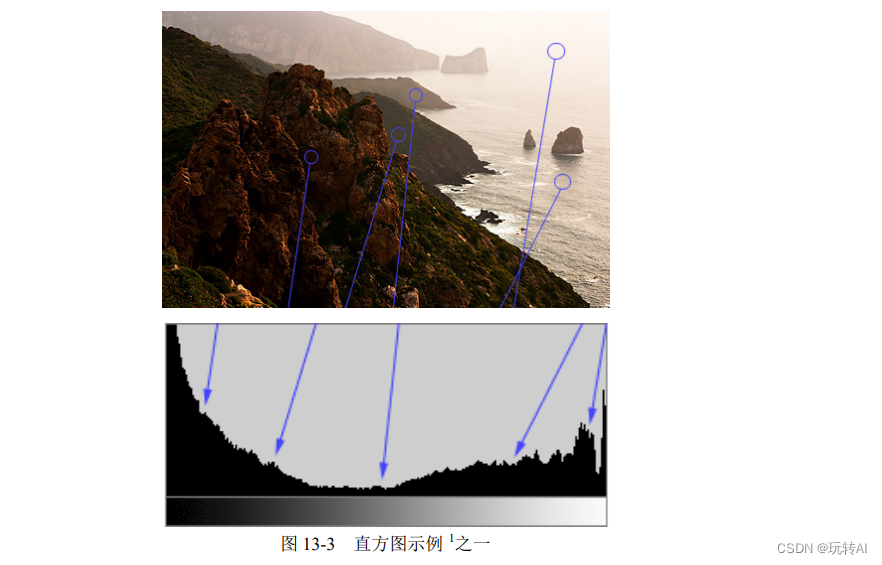
在这里插入图片描述

虽然 8 位的图像都具有 256 个灰度级（每一个像素可以有 256 个灰度值），但是属于不同灰度级的像素数量是很不一样的。

例如图 13-4，从图中可以看出，图像的不同部分直方图是不一样的。
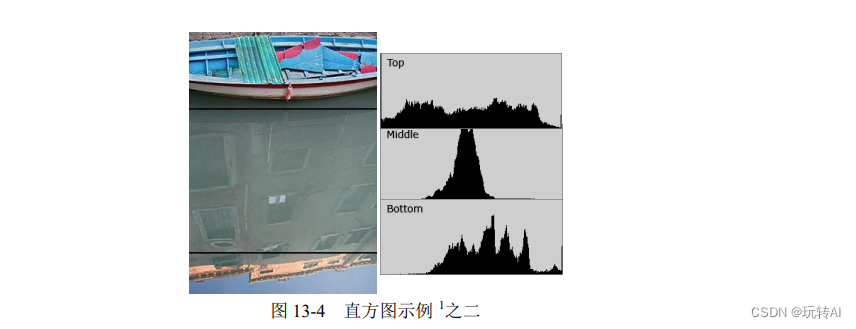
在这里插入图片描述

有时为了便于表示，也会采用归一化直方图。在归一化直方图中，x 轴仍然表示灰度级；y轴不再表示灰度级出现的次数，而是灰度级出现的频率。
例如，针对图 13-1，统计各个灰度级出现的频率：

灰度级出现的频率 = 灰度级出现的次数/总像素数

在图 13-1 中共有 9 个像素，所以统计结果如表 13-2 所示。

在这里插入图片描述

在归一化直方图中，各个灰度级出现的频率之和为 1。例如，本例中：

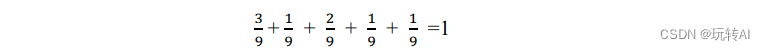
在这里插入图片描述
在绘制直方图时，将灰度级作为 x 轴数据处理，将其出现的频率作为 y 轴数据处理，则可知：

  • x 轴的数据为 x=[1 2 3 4 5]
  • y 轴的数据为 y=[3/9 1/9 2/9 1/9 2/9]

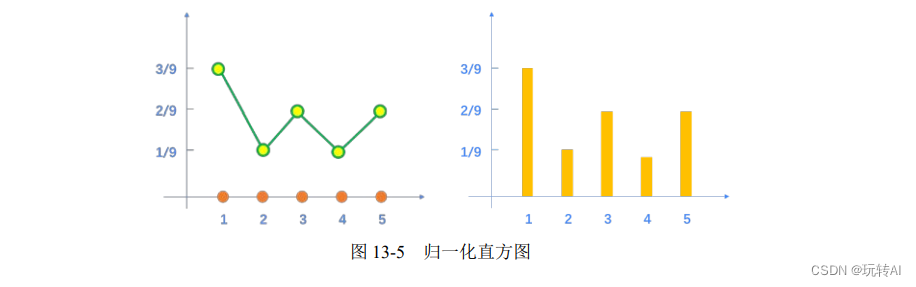
根据上述关系，可以绘制出如图 13-5 所示的归一化直方图。对比图 13-4 与图 13-5，可以看到，归一化直方图与直方图在外观上是一致的，只是 y 轴的标签不同而已。

本例中，在直方图内，y 轴显示的标签是 1、2、3；在归一化直方图中，y 轴显示的标签是 1/9、2/9、3/9。

在这里插入图片描述
在 OpenCV 的官网上，特别提出了要注意三个概念：DIMS、BINS、RANGE。

  • DIMS：表示在绘制直方图时，收集的参数的数量。一般情况下，直方图中收集的数据只有一种，就是灰度级。因此，该值为 1。
  • RANGE：表示要统计的灰度级范围，一般为[0, 255]。0 对应的是黑色，255 对应的是白色。
  • BINS：参数子集的数目。在处理数据的过程中，有时需要将众多的数据划分为若干个组，再进行分析。

例如，针对图 13-1 中的灰度级，你可能希望将两个像素值作为一组讨论。这样，整个灰度级被划分为三组，具体为{ {1,2} , {3,4} , {5} }。图 13-6 所示的是划分前后的直方图情况。

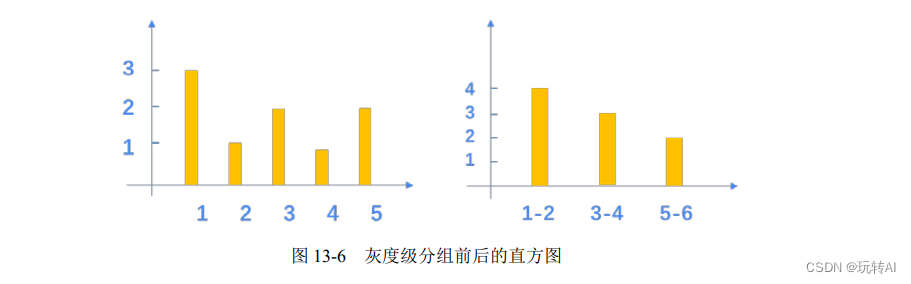
在这里插入图片描述

也可以按照上述方式对灰度图像进行划分。例如，在灰度图像中，将[0, 255]区间内的 256个灰度级，按照每 16 个像素一组划分为子集：

[0, 255] = [0, 15] ∪ [16, 31] ∪…∪[240, 255]

按照上述方式，整个灰度级范围可以划分为 16 个子集，具体为：

整个灰度级范围 = bin1 ∪ bin2 ∪…∪ bin16

子集划分完以后，某灰度图像生成的直方图如图 13-7 所示（图中的 b1 代表 bin1，b2 代表bin2，以此类推）。

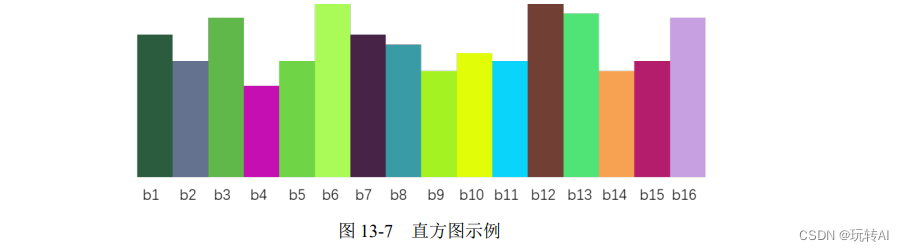
在这里插入图片描述
下面讨论 BINS 的值：

  • 针对图 13-1，在原始图像中，共有 5 个灰度级，其 BINS 值为 5。在以 2 个灰度级为一个小组划分子集后，得到 3 个子集，其 BINS 值为 3。
  • 针对灰度图像，灰度级区间为[0, 255]，共有 256 个灰度级，其 BINS 值为 256；在以 16个灰度级为一个小组划分子集后，其 BINS 值为 16。

说白了就是柱子的数量

绘制直方图

Python 的模块 matplotlib.pyplot 中的 hist()函数能够方便地绘制直方图，我们通常采用该函数直接绘制直方图（机器学习也用的这个）。除此以外，OpenCV 中的cv2.calcHist()函数能够计算统计直方图，还可以
在此基础上绘制图像的直方图。下面分别讨论这两种方式。

使用Numpy绘制直方图

模块 matplotlib.pyplot 提供了一个类似于 MATLAB 绘图方式的框架，可以使用其中的matplotlib.pyplot.hist()函数（以下简称为 hist()函数）来绘制直方图。

此函数的作用是根据数据源和灰度级分组绘制直方图。其基本语法格式为：

matplotlib.pyplot.hist(X，BINS)

其中两个参数的含义如下：

  • X：数据源，必须是一维的。图像通常是二维的，需要使用 ravel()函数将图像处理为一维数据源以后，再作为参数使用。

  • BINS：BINS 的具体值，表示灰度级的分组情况。

函数 ravel()的作用是将二维数组降维成一维数组。例如，有图像 a，其值为：

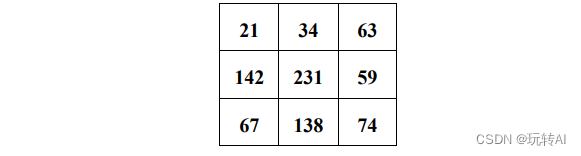
在这里插入图片描述
使用函数 ravel()对 a 进行处理：

b = a.ravel()

可以得到 b 为：
在这里插入图片描述

示例：使用 hist()函数绘制一幅图像的直方图。

在这里插入图片描述
代码如下：

import cv2
import matplotlib.pyplot as plt
o=cv2.imread("boat.jpg")
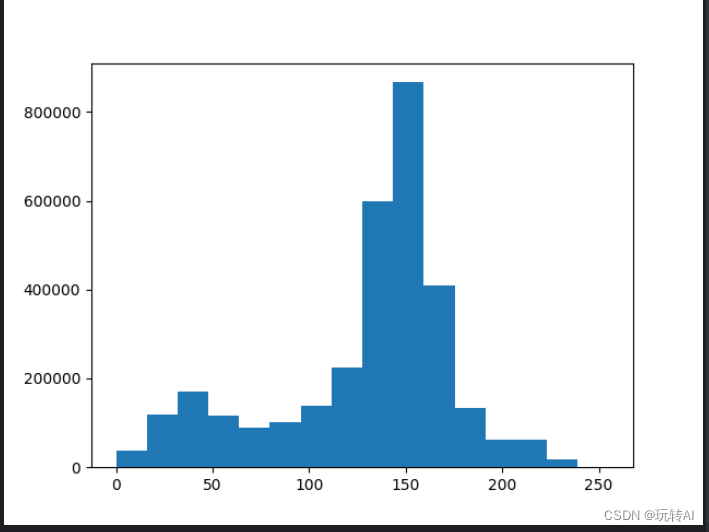
plt.hist(o.ravel(),256)
plt.show()

运行结果：

在这里插入图片描述

示例：使用函数 hist()将一幅图像的灰度级划分为 16 组后，绘制该图像的直方图。

将上面的255改成了16

import cv2
import matplotlib.pyplot as plt
o=cv2.imread("boat.jpg")
plt.hist(o.ravel(),16)
plt.show()

在这里插入图片描述

使用OpenCV绘制直方图

OpenCV 提供了函数 cv2.calcHist()用来计算图像的统计直方图，该函数能统计各个灰度级的像素点个数。利用matplotlib.pyplot 模块中的 plot()函数，可以将函数 cv2.calcHist()的统计结果绘制成直方图

1．用cv2.calcHist()函数统计图像直方图信息
函数 cv2.calcHist()用于统计图像直方图信息，其语法格式为：

hist = cv2.calcHist( images, channels, mask, histSize, ranges, accumulate )

函数中返回值及参数的含义为：

  • hist：返回的统计直方图，是一个一维数组，数组内的元素是各个灰度级的像素个数。

  • images：原始图像，该图像需要使用“[ ]”括起来。

  • channels：指定通道编号。通道编号需要用“[ ]”括起来，如果输入图像是单通道灰度图像，该参数的值就是[0]。对于彩色图像，它的值可以是[0]、[1]、[2]，分别对应通道B、G、R。

  • mask：掩模图像。当统计整幅图像的直方图时，将这个值设为 None。当统计图像某一部分的直方图时，需要用到掩模图像。

  • histSize：BINS 的值，该值需要用“[ ]”括起来。例如，BINS 的值是 256，需要使用“[256]”作为此参数值。

  • ranges：即像素值范围。例如，8 位灰度图像的像素值范围是[0, 255]。

  • accumulate：累计（累积、叠加）标识，默认值为 False。如果被设置为 True，则直方图在开始计算时不会被清零，计算的是多个直方图的累积结果，用于对一组图像计算直方
    图。该参数允许从多个对象中计算单个直方图，或者实时更新直方图。该参数是可选的，一般情况下不需要设置。

示例：使用 cv2.calcHist()函数计算一幅图像的统计直方图结果，并观察得到的统计直方图信息。

代码如下：


import cv2
img=cv2.imread("boat.jpg")
hist = cv2.calcHist([img],[0],None,[16],[0,255])
print(type(hist))
print(hist.shape)
print(hist.size)
print(hist)

运行结果如下：
需要注意，在本例的 cv2.calcHist()函数中：

  • 第 1 个参数“[img]”表示要绘制直方图的原始图像，是使用“[ ]”括起来的。
  • 第 2 个参数表示要统计哪个通道的直方图信息。本例中读取的 img 是灰度图像，所以使
    用“[0]”来表示。
  • 第 3 个参数是掩模图像，在本例中的值为“None”，表示计算整幅图像的直方图。
  • 第 4 个参数“[16]”表示 BINS 的值是 16，也就是分了16组
  • 第 5 个参数“[0, 255]”表示灰度级的范围是[0, 255]。
<class 'numpy.ndarray'>
(16, 1)
16
[[ 12575.][ 39591.][ 56651.][ 38932.][ 29997.][ 33472.][ 46033.][ 74555.][199718.][288966.][136663.][ 44440.][ 20355.][ 20691.][  5578.][   344.]]

示例:绘制统计直方图

import cv2
from matplotlib import pyplot as pltimg=cv2.imread("boat.jpg")
hist = cv2.calcHist([img],[0],None,[16],[0,255])plt.plot(hist,color='b')
plt.show()

运行结果：
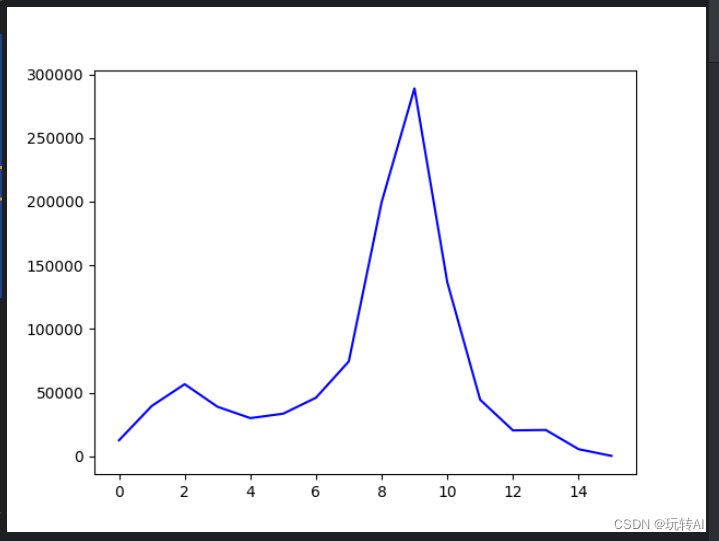
在这里插入图片描述

以上都是将图像进行直方图展示函数，下面来讲下直方图在图像处理中的应用函数。

直方图均衡化

如果一幅图像拥有全部可能的灰度级，并且像素值的灰度均匀分布，那么这幅图像就具有高对比度和多变的灰度色调，灰度级丰富且覆盖范围较大。在外观上，这样的图像具有更丰富的色彩，不会过暗或过亮。

图 13-22 展示了对一幅图像进行直方图均衡化前后的对比，左图是原始图像，比较暗；右图是均衡化后的图像，色彩比较均衡。

在这里插入图片描述

在 OpenCV 的官网上，对图像均衡化（即直方图均衡化）前后的直方图进行了对比，如图13-23 所示。其中，左图是原始图像的直方图，可以看到灰度级集中在中间，图像中没有较暗和较亮的像素点；右图是对原图均衡化后的直方图，像素分布更均衡。

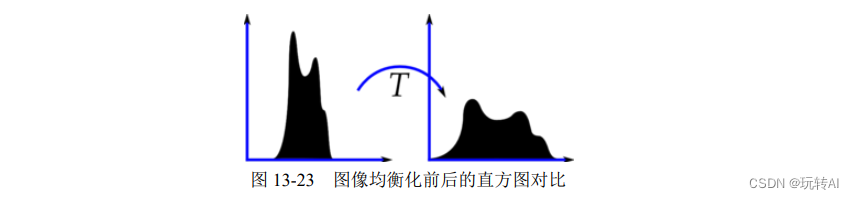
在这里插入图片描述

直方图均衡化的主要目的是将原始图像的灰度级均匀地映射到整个灰度级范围内，得到一个灰度级分布均匀的图像。这种均衡化，既实现了灰度值统计上的概率均衡，也实现了人类视觉系统（Human Visual System，HVS）上的视觉均衡。

直方图均衡化函数

OpenCV 使用函数 cv2.equalizeHist()实现直方图均衡化。该函数的语法格式为：

dst = cv2.equalizeHist( src )

式中：

  • dst 是直方图均衡化处理的结果。
  • src 是 8 位单通道原始图像。

示例：使用函数 cv2.equalizeHist()实现直方图均衡化。

原图：
在这里插入图片描述
代码如下：

#-----------导入使用的模块---------------
import cv2
import matplotlib.pyplot as plt
#-----------读取原始图像---------------
img = cv2.imread('equ.bmp',cv2.IMREAD_GRAYSCALE)
#-----------直方图均衡化处理---------------
equ = cv2.equalizeHist(img)
#-----------显示均衡化前后的图像---------------
cv2.imshow("original",img)
cv2.imshow("result",equ)
#-----------显示均衡化前后的直方图---------------
plt.figure("原始图像直方图") #构建窗口
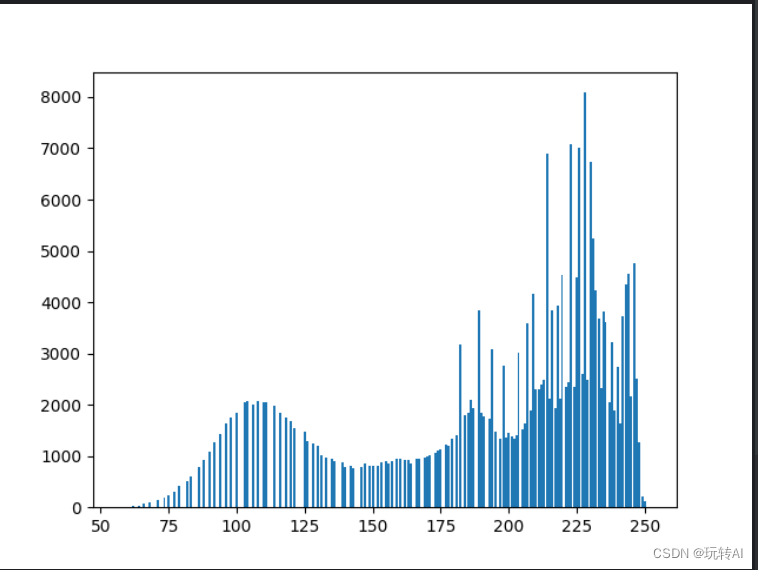
plt.hist(img.ravel(),256)
plt.figure("均衡化结果直方图") #构建新窗口
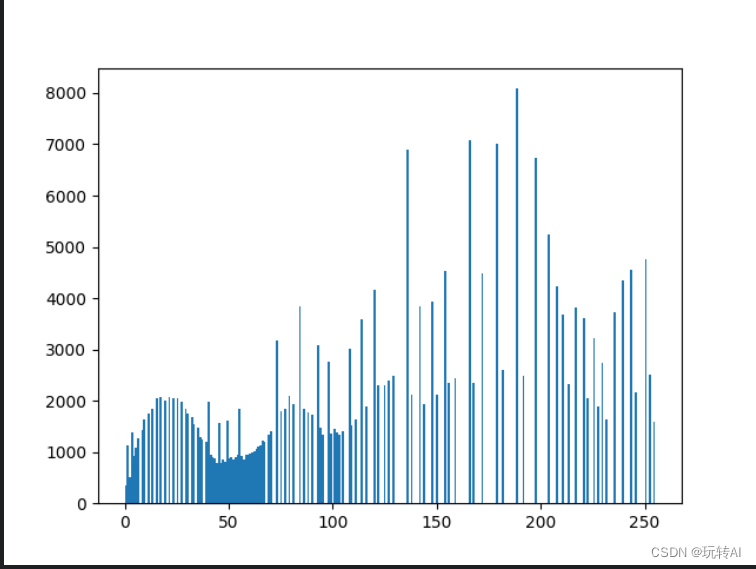
plt.hist(equ.ravel(),256)
plt.show()
#----------等待释放窗口---------------------
cv2.waitKey()
cv2.destroyAllWindows()

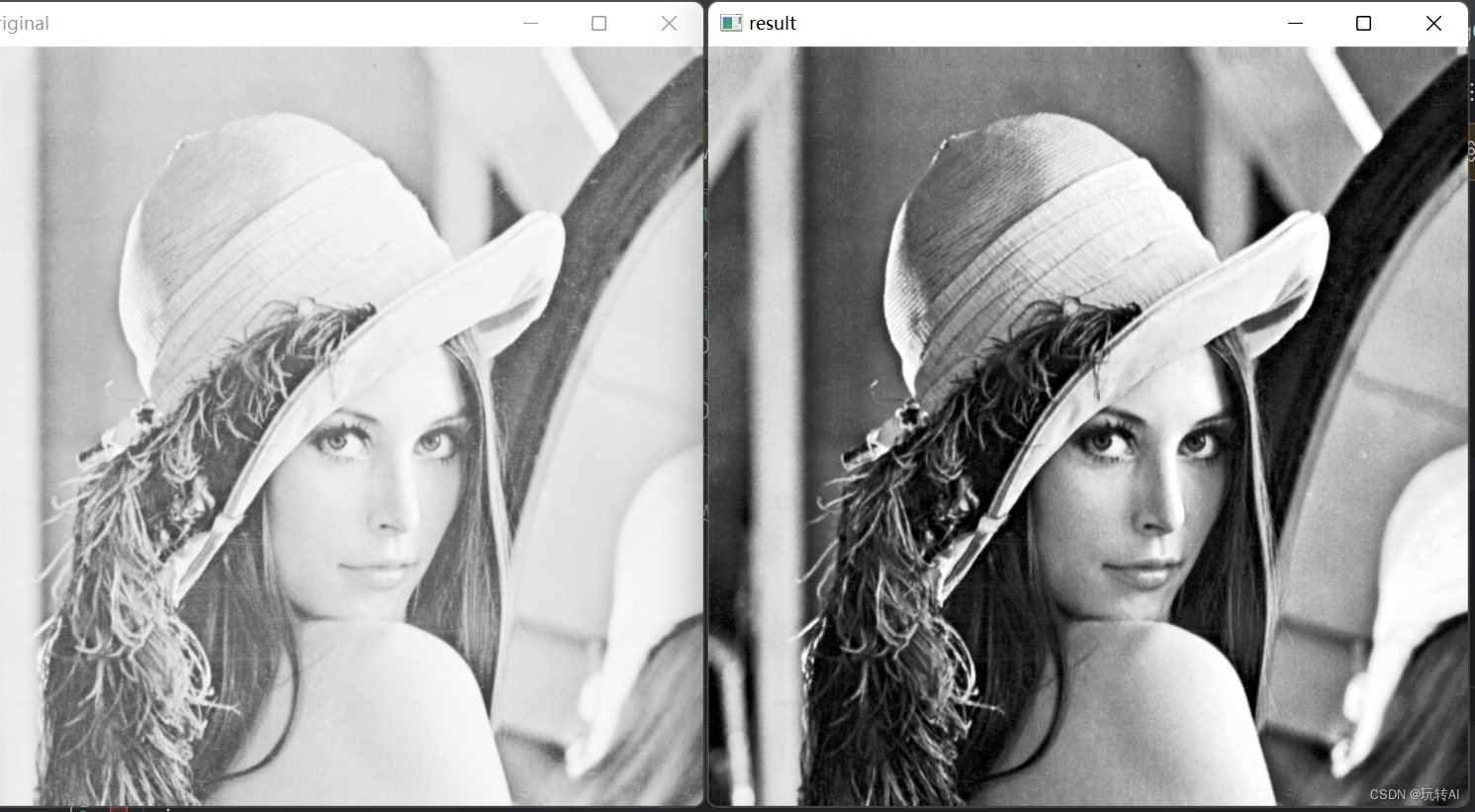
在这里插入图片描述
结果中可以看到对比很明显：在直方图均衡化之前，图像整体比较
亮；均衡化以后，图像的亮度变得比较均衡。而两幅图像的直方图的对比，则不太明显。这实际上体现了，均衡化是指综合考虑了统计概率和 HVS 的结果。

在这里插入图片描述
在这里插入图片描述
下面做简单的说明：

  • 原始图像的直方图，大部分的像素值集中在右侧（线条密集）。这说明图像中位于[200,255]区间的像素点很多，图像比较亮。

  • 在均衡化后的直方图中，左侧的像素点比较密集而右侧的相对比较稀疏。但是，实际上人眼并不能明显感受到像素值的细微差别，所以我们可以将相近的像素值看成同一个像素值，这样就会得到类似于图 13-29 的直方图。此时，直方图内灰度级的分布就比较均衡了，是均衡一致的直方图。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/92030.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

力扣初级算法（数组拆分）

力扣初级算法（数组拆分）

力扣初级算法&#xff08;数组拆分&#xff09; 每日一算法&#xff1a; 力扣初级算法&#xff08;数组拆分&#xff09; 学习内容&#xff1a; 1.问题描述 给定长度为 2n 的整数数组 nums &#xff0c;你的任务是将这些数分成 n 对, 例如 (a1, b1), (a2, b2), …, (an, bn) …
阅读更多...
pytest自动生成测试类 demo

pytest自动生成测试类 demo

一、 pytest自动生成测试类 demo # -*- coding:utf-8 -*- # Author: 喵酱 # time: 2023 - 08 -15 # File: test4.py # desc: import pytest import unittest# 动态生成测试类def create_test_class(class_name:str, test_cases:list) -> type:"""生成测试类…
阅读更多...
流程挖掘in汽车丨宝马的流程效能提升实例

流程挖掘in汽车丨宝马的流程效能提升实例

汽车行业在未来10年里&#xff0c;可能会面临比过去50年更多的变化。电动化、智能化、共享化和自动驾驶等方面的趋势可能给企业流程带来以下挑战&#xff1a; 供应链管理-电动化和智能化的发展可能导致供应链中的零部件和系统结构发生变化&#xff0c;企业需要重新评估和优化供…
阅读更多...
结构体指针变量的使用

结构体指针变量的使用

1、结构体指针的引用 #include<iostream> using namespace std;struct Student {int num;char name[32]; }; int main() {struct Student stu {1,"张三"};struct Student* p &stu;system("pause"); return 0; } 2、通过结构体指针访问结构体…
阅读更多...
vue所有UI库通用）tree-select 下拉多选（设置 maxTagPlaceholder 隐藏 tag 时显示的内容，支持鼠标悬浮展示更多

vue所有UI库通用）tree-select 下拉多选（设置 maxTagPlaceholder 隐藏 tag 时显示的内容，支持鼠标悬浮展示更多

如果可以实现记得点赞分享&#xff0c;谢谢老铁&#xff5e; 1.需求描述 引用的下拉树形结构支持多选&#xff0c;限制选中tag的个数&#xff0c;且超过制定个数&#xff0c;鼠标悬浮展示更多已选中。 2.先看下效果图 3.实现思路 首先根据API文档&#xff0c;先设置maxTagC…
阅读更多...
嵌入式 C 语言程序数据基本存储结构

嵌入式 C 语言程序数据基本存储结构

一、5大内存分区 内存分成5个区&#xff0c;它们分别是堆、栈、自由存储区、全局/静态存储区和常量存储区。 1、栈区(stack)&#xff1a;FIFO就是那些由编译器在需要的时候分配&#xff0c;在不需要的时候自动清除的变量的存储区。里面的变量通常是局部变量、函数参数等。 ​…
阅读更多...
什么是层叠上下文（stacking context）？它是如何形成的？

什么是层叠上下文（stacking context）？它是如何形成的？

聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 层叠上下文&#xff08;Stacking Context&#xff09;是什么&#xff1f;⭐ 层叠上下文的形成⭐ 写在最后 ⭐ 专栏简介 前端入门之旅&#xff1a;探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎…
阅读更多...
Vue2（组件开发）

Vue2（组件开发）

目录 前言一&#xff0c;组件的使用二&#xff0c;插槽slot三&#xff0c;refs和parent四&#xff0c;父子组件间的通信4.1&#xff0c;父传子 &#xff1a;父传子的时候&#xff0c;通过属性传递4.2&#xff0c;父组件监听自定义事件 五&#xff0c;非父子组件的通信六&#x…
阅读更多...
网络安全攻防实战：探索互联网发展史

网络安全攻防实战：探索互联网发展史

大家好&#xff0c;我是沐尘而生。 互联网发展史&#xff1a;数字世界的壮阔画卷 从早期的ARPANET到今天的万物互联&#xff0c;互联网经历了漫长的发展过程。然而&#xff0c;随着技术的进步&#xff0c;网络安全问题也随之而来。我们不仅要探索互联网的壮阔历程&#xff0c;…
阅读更多...
浅谈 EMP-SSL + 代码解读：自监督对比学习的一种极简主义风

浅谈 EMP-SSL + 代码解读：自监督对比学习的一种极简主义风

论文链接&#xff1a;https://arxiv.org/pdf/2304.03977.pdf 代码&#xff1a;https://github.com/tsb0601/EMP-SSL 其他学习链接&#xff1a;突破自监督学习效率极限&#xff01;马毅、LeCun联合发布EMP-SSL&#xff1a;无需花哨trick&#xff0c;30个epoch即可实现SOTA 主要…
阅读更多...
【需求输出】流程图输出

【需求输出】流程图输出

文章目录 1、什么是流程图2、绘制流程图的工具和基本要素3、流程图的分类和应用场景4、如何根据具体场景输出流程图 1、什么是流程图 2、绘制流程图的工具和基本要素 3、流程图的分类和应用场景 4、如何根据具体场景输出流程图
阅读更多...
如何能够写出带货的爆文？

如何能够写出带货的爆文？

网络推广这个领域&#xff0c;公司众多价格差别很大&#xff0c;就拿软文文案这块来讲&#xff0c;有人报价几十块&#xff0c;也有人报价几千块。作为企业的营销负责人往往会被价格吸引&#xff0c;比价择优选用&#xff0c;结果写出来的文案不满意&#xff0c;修改也无从入手…
阅读更多...
LVS简介及LVS-DR搭建

LVS简介及LVS-DR搭建

目录 一. LVS简介&#xff1a; 1.简介 2. LVS工作模式&#xff1a; 3. LVS调度算法&#xff1a; 4. LVS-DR集群介绍&#xff1a; 二.LVS-DR搭建 1.RS配置 1&#xff09;两台RS&#xff0c;需要下载好httpd软件并准备好配置文件 2&#xff09;添加虚拟IP&#xff08;vip&…
阅读更多...
openeuler服务器 ls 和ll 命令报错 command not found...

openeuler服务器 ls 和ll 命令报错 command not found...

在openeuler服务器执行 ls 和ll 命令报错 command not found... 大概是系统环境变量导致的问题。 我在安装redis是否没有安装成功后就出现了这样的情况。编辑profile文件没有写正确&#xff0c;导致在命令行下ls 和 ll 等命令不能够识别。 重新设置一下环境变量。 export PAT…
阅读更多...
excel快速选择数据、选择性粘贴、冻结单元格

excel快速选择数据、选择性粘贴、冻结单元格

一、如何快速选择数据 在excel中&#xff0c;希望选择全部数据&#xff0c;通常使用鼠标选择数据然后往下拉&#xff0c;当数据很多时&#xff0c;也可单击单元格使用ctrl A选中全部数据&#xff0c;此外&#xff0c;具体介绍另一种方法。 操作&#xff1a;ctrl shift 方向…
阅读更多...
【第三阶段】kotlin语言空合并操作符

【第三阶段】kotlin语言空合并操作符

1.空操作符&#xff1f;&#xff1a; xxx?:“如果是null执行” 如果xxx是null&#xff0c;就执行?:后面的逻辑&#xff0c;如果不是null就执行&#xff1f;&#xff1a;前面的逻辑&#xff0c;后面的不在执行 fun main() {var name:String?"kotlin" namenullvar …
阅读更多...
MAC环境，在IDEA执行报错java: -source 1.5 中不支持 diamond 运算符

MAC环境，在IDEA执行报错java: -source 1.5 中不支持 diamond 运算符

Error:(41, 51) java: -source 1.5 中不支持 diamond 运算符 (请使用 -source 7 或更高版本以启用 diamond 运算符) 进入设置 修改java版本 pom文件中加入 <plugin><groupId>org.apache.maven.plugins</groupId><artifactId>maven-compiler-plugin&l…
阅读更多...
docker发展历史

docker发展历史

docker 一、docker发展历史很久以前2013年2014年2015年2016年2017年2018年2019年及未来 二、 docker概述定义&#xff1a;docker底层运行原理:docker简述核心概念容器特点Docker与虚拟机的区别: 三、容器在内核中支持两种重要技术四、namespace的六项隔离五、虚拟化产品有哪些1…
阅读更多...
ChatGPT等人工智能编写文章的内容今后将成为常态

ChatGPT等人工智能编写文章的内容今后将成为常态

BuzzFeed股价上涨200%可能标志着“转向人工智能”媒体趋势的开始。 周四&#xff0c;一份内部备忘录被华尔街日报透露BuzzFeed正计划使用ChatGPT聊天机器人-风格文本合成技术来自OpenAI&#xff0c;用于创建个性化盘问和将来可能的其他内容。消息传出后&#xff0c;BuzzFeed的…
阅读更多...
QGIS3.28的二次开发九：添加矢量要素

QGIS3.28的二次开发九：添加矢量要素

对矢量要素的编辑是 GIS 软件很重要的功能点之一&#xff0c;也是最难实现的功能点之一。编辑矢量要素涉及到很多方面的考虑&#xff0c;包括且不限于矢量要素的几何类型&#xff0c;拓扑关系&#xff0c;构成要素的节点的增删改&#xff0c;编辑会话 (session) 的启动、回溯和…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023