1 引言

在前面的文章中已经介绍了介绍了一系列激活函数 (Sigmoid、Tanh、ReLU、Leaky ReLU、PReLU、Swish、ELU、SELU、GELU、Softmax、Softplus、Mish、Maxout、HardSigmoid、HardTanh、Hardswish、HardShrink、SoftShrink、TanhShrink、RReLU、CELU、ReLU6、GLU、SwiGLU、GTU、Bilinear、ReGLU、GEGLU、Softmin、Softmax2d、Logsoftmax)。在这篇文章中，会接着上文提到的众多激活函数继续进行介绍，给大家带来更多不常见的激活函数的介绍。这里放一张激活函数的机理图：
在这里插入图片描述

最后，对于文章中没有提及到的激活函数，大家可以通过评论指出，作者会在后续的文章中进行添加补充。

2 激活函数

2.1 Identity激活函数

Identity 激活函数，也称为线性激活函数，是一种最简单的激活函数之一。它的作用是将输入直接传递到输出，不进行任何变换。换句话说，当使用 Identity 激活函数时，神经网络的输出将与输入完全相同，这意味着任何线性组合或变换都不会发生。其数学表达式和数学图像分别如下所示：
$I d e n t i t y (x) = x$ 在这里插入图片描述
优点：

简单、易于理解和计算：线性激活函数是可微分的，这使得基于梯度的优化方法如梯度下降法可以很好地运行。

缺点：

无非线性：没有办法提供非线性，无论堆叠多少层，最后的输出仍然是输入的线性组合，这限制了模型的表达能力。不能处理复杂的非线性问题，对于深度神经网络并不适用。

通常用于连续性数值的回归预测中，在深度网络中很少应用。。。

2.2 LogSigmoid激活函数

LogSigmoid激活函数是在 Sigmoid 激活函数的基础上进行 Log 操作。其数学表达式和数学图像分别如下所示：
$\ln\left(\frac{1}{1 + \exp(-x)}\right)$ 在这里插入图片描述

优点：

平滑性：与 Sigmoid 相似，LogSigmoid 激活函数也是平滑的，但在输入远离零时，其输出变化更为平缓，有助于梯度的稳定传播。
控制输出范围：LogSigmoid 的输出范围在负无穷到 0 之间，可以将输入数据映射到一个更小的范围。

缺点：

梯度消失问题：虽然在输入远离零时梯度变化较为平缓，但仍然可能会遇到梯度消失的问题，特别是在深层网络中。

考虑到Sigmoid当前的使用环境，LogSigmoid在当前也很少使用。。。

2.3 Bent Identity激活函数

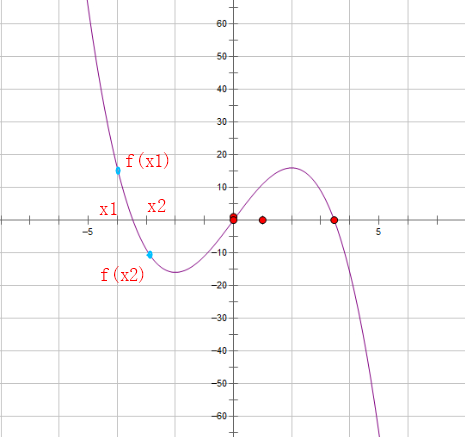
激活函数 Bent Identity 是介于 Identity 与 ReLU 之间的一种折衷选择。它允许非线性行为，尽管其非零导数有效提升了学习并克服了与 ReLU 相关的静默神经元的问题。由于其导数可在 1 的任意一侧返回值，因此它可能容易受到梯度爆炸和消失的影响。其数学表达式和数学图像分别如下所示：
$\frac{\sqrt{x^2 + 1} - 1}{2} + x$
在这里插入图片描述

优点：

平滑性： Bent Identity激活函数是一个平滑的函数，这意味着它在整个输入范围内都具有连续的导数。这有助于稳定的梯度传播，可以在训练神经网络时避免梯度爆炸或梯度消失问题。
适度非线性： Bent Identity激活函数在输入为负时呈现线性增长，而在输入为正时呈现较缓的非线性增长。这可以使其在一些任务中具有适度的非线性表达能力，从而更好地捕捉输入数据中的特征。
输出范围： Bent Identity激活函数的输出范围是负无穷到正无穷，这在某些情况下可能有用。与一些其他激活函数（如Sigmoid或Tanh）相比，它不会限制输出的范围，可能更适合处理具有广泛范围的数据。

缺点：

相对复杂： Bent Identity激活函数的表达式比较复杂，可能会在实现和计算上引入一些额外的复杂性。这可能会影响训练和推理的效率。
较少的使用： Bent Identity激活函数相对较少被广泛使用，因此关于其性能和适用性的实证研究可能相对有限。这可能导致难以确定在特定问题上是否比其他更常见的激活函数表现更好。
调参复杂性：选择激活函数涉及到一些超参数的调优。由于Bent Identity不像一些更常见的激活函数那样广泛使用，可能需要更多的实验来找到最佳的超参数设置。

总体而言：Identity和ReLU的结合并没有带来很好的效果，整体使用情况还不如ReLU激活函数。。。