[NOI2015] 程序自动分析
题目描述
在实现程序自动分析的过程中,常常需要判定一些约束条件是否能被同时满足。
考虑一个约束满足问题的简化版本:假设 x 1 , x 2 , x 3 , ⋯ x_1,x_2,x_3,\cdots x1,x2,x3,⋯ 代表程序中出现的变量,给定 n n n 个形如 x i = x j x_i=x_j xi=xj 或 x i ≠ x j x_i\neq x_j xi=xj 的变量相等/不等的约束条件,请判定是否可以分别为每一个变量赋予恰当的值,使得上述所有约束条件同时被满足。例如,一个问题中的约束条件为: x 1 = x 2 , x 2 = x 3 , x 3 = x 4 , x 4 ≠ x 1 x_1=x_2,x_2=x_3,x_3=x_4,x_4\neq x_1 x1=x2,x2=x3,x3=x4,x4=x1,这些约束条件显然是不可能同时被满足的,因此这个问题应判定为不可被满足。
现在给出一些约束满足问题,请分别对它们进行判定。
输入格式
输入的第一行包含一个正整数 t t t,表示需要判定的问题个数。注意这些问题之间是相互独立的。
对于每个问题,包含若干行:
第一行包含一个正整数 n n n,表示该问题中需要被满足的约束条件个数。接下来 n n n 行,每行包括三个整数 i , j , e i,j,e i,j,e,描述一个相等/不等的约束条件,相邻整数之间用单个空格隔开。若 e = 1 e=1 e=1,则该约束条件为 x i = x j x_i=x_j xi=xj。若 e = 0 e=0 e=0,则该约束条件为 x i ≠ x j x_i\neq x_j xi=xj。
输出格式
输出包括 t t t 行。
输出文件的第 k k k 行输出一个字符串 YES 或者 NO(字母全部大写),YES 表示输入中的第 k k k 个问题判定为可以被满足,NO 表示不可被满足。
样例 #1
样例输入 #1
2
2
1 2 1
1 2 0
2
1 2 1
2 1 1
样例输出 #1
NO
YES
样例 #2
样例输入 #2
2
3
1 2 1
2 3 1
3 1 1
4
1 2 1
2 3 1
3 4 1
1 4 0
样例输出 #2
YES
NO
提示
【样例解释1】
在第一个问题中,约束条件为: x 1 = x 2 , x 1 ≠ x 2 x_1=x_2,x_1\neq x_2 x1=x2,x1=x2。这两个约束条件互相矛盾,因此不可被同时满足。
在第二个问题中,约束条件为: x 1 = x 2 , x 1 = x 2 x_1=x_2,x_1 = x_2 x1=x2,x1=x2。这两个约束条件是等价的,可以被同时满足。
【样例说明2】
在第一个问题中,约束条件有三个: x 1 = x 2 , x 2 = x 3 , x 3 = x 1 x_1=x_2,x_2= x_3,x_3=x_1 x1=x2,x2=x3,x3=x1。只需赋值使得 x 1 = x 2 = x 3 x_1=x_2=x_3 x1=x2=x3,即可同时满足所有的约束条件。
在第二个问题中,约束条件有四个: x 1 = x 2 , x 2 = x 3 , x 3 = x 4 , x 4 ≠ x 1 x_1=x_2,x_2= x_3,x_3=x_4,x_4\neq x_1 x1=x2,x2=x3,x3=x4,x4=x1。由前三个约束条件可以推出 x 1 = x 2 = x 3 = x 4 x_1=x_2=x_3=x_4 x1=x2=x3=x4,然而最后一个约束条件却要求 x 1 ≠ x 4 x_1\neq x_4 x1=x4,因此不可被满足。
【数据范围】
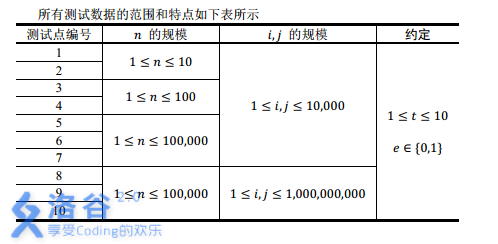
注:实际上 n ≤ 1 0 6 n\le 10^6 n≤106 。
分析
由于只有=和!=两种,可以考虑利用=建立关系,利用!=查看是否合法,这样,我们需要多个集合,把相等的元素的下标存入集合分类,实现此操作,使用并查集即可。
代码
#include<bits/stdc++.h>
using namespace std;
const long long M = 1e6 + 10;
int f[M],li[M<<2];int n,tot=0;
int find(int x){return x==f[x]?x:f[x]=find(f[x]);}
void merge(int x,int y){x=find(x),y=find(y),f[x]=y;
}
struct node{int x,y,e;
}a[M];
struct cmp{bool operator () (const node& a,const node& b){return a.e>b.e;}
};
istream& operator >> (istream& in,node &a){in>>a.x>>a.y>>a.e;return in;
}
void init(int n){for (int i=0;i<=n;i++) f[i]=i;
}
void Discretization(){sort(li,li+tot);int res=unique(li,li+tot)-li;for (int i=1;i<=n;i++){a[i].x=lower_bound(li,li+res,a[i].x)-li;a[i].y=lower_bound(li,li+res,a[i].y)-li;}init(res);
}
signed main() {int T;cin>>T;while (T--){cin>>n;tot=0;for (int i=1;i<=n;i++){cin>>a[i];li[tot++]=a[i].x,li[tot++]=a[i].y;}Discretization();sort(a+1,a+n+1,cmp());bool ff=1;for (int i=1;i<=n;i++){int xx=find(a[i].x),yy=find(a[i].y);if (a[i].e)f[xx]=yy;else if (xx==yy){ cout<<"NO"<<endl;ff=0;break;}}if(ff) cout<<"YES"<<endl;}return 0;
}
代码解析
signed main() {int T;cin>>T;while (T--){cin>>n;tot=0;for (int i=1;i<=n;i++){cin>>a[i];li[tot++]=a[i].x,li[tot++]=a[i].y;}Discretization();sort(a+1,a+n+1,cmp());bool ff=1;for (int i=1;i<=n;i++){int xx=find(a[i].x),yy=find(a[i].y);if (a[i].e)f[xx]=yy;else if (xx==yy){ cout<<"NO"<<endl;ff=0;break;}}if(ff) cout<<"YES"<<endl;}return 0;
}
只看主函数,思路不难理解,但Discretization();与li的意义很难看出,读者若尝试删除它们,会得到RE或WA,这是因为 n ≤ 1 0 6 n\le 10^6 n≤106但 i , j ≤ 1 0 9 i,j\le 10^9 i,j≤109,下标根本存不下,这时需要离散化
9 6 7 1
3 1 2 0
观察上面的数据第二行存储了第一行排序后所在下标,虽然数据改变了,但可以完成比较大小和比较相等操作,这是离散化
void Discretization(){sort(li,li+tot);int res=unique(li,li+tot)-li;for (int i=1;i<=n;i++){a[i].x=lower_bound(li,li+res,a[i].x)-li;a[i].y=lower_bound(li,li+res,a[i].y)-li;}init(res);
}
笔者用了简单的离散化,复制原数组,排序,去重,最后二分读下标时间复杂度 O ( n l o g n ) O(n log n) O(nlogn)